从网络暴力的产生、社会舆论的形成,到疾病的传播和椋鸟群飞的奇观,共识是其集体行为的根源,但产生这些行为的系统实际上倾向于脱离共识而运作。动物、人类或集群机器人之间基于共识的集体行为是如何涌现的?先前的研究已经发现,社交网络上的这种行为传播表现出从简单传染(即基于成对的交互)到复杂传染(即涉及社会影响和强化)的转变。最新发表在Nature Communications 的一项研究发现,传染的性质(简单或复杂)与传播行为的内在速度密切相关,网络拓扑强烈影响行为传播的有效性。这项研究结果不仅可以为集体行为涌现的实证提供新方向,也可以用于改进工程网络系统(如物联网、集群机器人)的设计,也能为舆情管理和疫情防控提供借鉴。
研究领域:复杂网络,社交网络,涌现,非线性现象,集体行为

论文题目:
Transition from simple to complex contagion in collective decision-making
论文链接:
一、集体行为的涌现:从简单传染到复杂传染
无论鸟群飞舞这样的自然现象,还是舆论传播这样的人类复杂系统,都是基于主体之间的相互连接,并通过网络连接协调特定的行为过程。这种高层次的复杂网络包含各种不同的系统,产生了一系列涌现行为,如椋鸟群飞、网络暴力形成、疾病传播、电网的级联故障和集群机器人系统的目标追踪等等。人们发现,这种集体动力学在很大程度上取决于基础的网络拓扑结构,它为行为变化的有效传播提供了条件。
行为的变化在社会系统中的传播,或者说在工程网络中的传播,被认为类似于传染过程,它可以是“简单的”也可以是“复杂的”。在简单传染的情况下,行为通过单一的接触或互动来传播。另一方面,如果行为的传播需要个体通过两个或更多的来源强化来使其感染,那么这种传染就是复杂传染。集体行为的涌现主要是从简单传染到复杂传染的转变过程。
阈值模型(Threshold model)一直是最主要的描述各种复杂传染过程的建模框架,例如健康措施和创新的采用,以及社交媒体上虚假信息的传播。阈值模型假设主体处于“激活”和“未激活”两种状态,如果社交网络上一个主体被激活的邻居比例大于给定阈值,则该主体就会被激活。阈值模型完全符合复杂传染的最初定义,即当阈值超过对应于有一个以上激活邻居的值时,就会发生从简单传染到复杂传染的转变。
在阈值模型的框架内,被传播的行为具有激活和未激活的二元性质。这种简化显然有利于跟踪从一个主体到整个系统的行为传染。这一特点很好地满足了研究涉及两个选项的集体决策过程的目的,如投票和创新的采用与否。然而,众多的集体决策更为复杂,涉及到一系列选择,而不仅仅只有二元选项。并且,在考虑缺乏阈值的非线性行为模型时,“激活”这一关键概念可能不那么明显,那么就很难使用复杂传染概念解释这种集体行为。共识是集体行为的根源,因此需要构建一种基于共识的、更为一般的模型,这种模型可以解释除二元决策行为外,其他更复杂的、不包含阈值的集体决策行为。
研究发现,鱼群的规避行为和椋鸟的集体转向等,这些动物主体间互动的一个关键因素是行为方向的“对齐(alignment)”,然而这种基于“方向共识”的模型并不能很好地用于跟踪集体行为级联效应,因为与基于二元阈值的模型不同,这些动物状态具有非二元性质。与所有行为学模型一样,即使有可能以某些方式修改模型主体之间的互动关系,也几乎不可能完全控制主体的所有行为。
然我们对动物的群体行为缺乏充分的理解,但生物学家发现人类和动物的社会行为之间存在着深刻的相似性。最近对鱼类和鸟类的大规模实证研究揭示了个体间错综复杂的互动模式,这些模式是整个群体集体行为涌现的基础。鱼群的网络属性(它们的“社会连通性”)是造成鱼群在面临危险时高度集体反应的主要因素。因此,复杂网络的拓扑结构在解释阈值模型时起着关键的作用。简单传染因网络距离短而增强,复杂传染则因高水平的聚集而放大。通过采用与多机器人系统(multirobot system)类似的方法,人们可以改变局部互动规则,即改变互动网络的拓扑结构,比较信息传递的有效性,进而分析集体行为的涌现过程。
这项研究使用领导者-追随者共识模型(leader–follower consensus),研究由单一领导者作为可调整频率的刺激物时,一群网络化主体的行为传染问题。研究发现,通过改变网络拓扑结构,快节奏的刺激物以复杂传染的方式传播。当改变刺激的速度(即频率)时,研究者发现了从简单传染到复杂传染的过渡。当改变交互网络的拓扑特征(如聚集系数、平均最短路径等)时,这种过渡是显而易见的。此外,研究者使用一个由10个联网主体组成的机器人实验测试平台,执行类似于在成群椋鸟的集体转向中观察到的“方向共识”,发现在快节奏刺激的驱动下,行为传播具有复杂传染的特征。
这些结果具有深远的影响。首先,他们将简单传染到复杂传染的概念从仅限于基于二元阈值的线性模型(linear threshold model,LTM),扩展到基于连续共识的连续阈值模型(continuous threshold model,CTM)。其次,这些结果表明,简单或复杂传染的性质与行为传播的类型直接相关,更具体地说,与其内在动态的速度有关。
二、结论
1、传播速度影响从简单传染到复杂传染的过渡
如以下公式所示,复杂传染最初是通过典型的线性阈值模型来发现和研究的,当活跃的网络邻居的比例超过一定的阈值θ时,节点就会变得活跃。人们对理解θ和网络拓扑结构之间的相互作用以实现全局行为涌现(即产生99%节点的激活)给予了极大的关注。已有研究反复证明,与简单传染相比,复杂传染在聚集系数高的网络上传播得更快、更远。
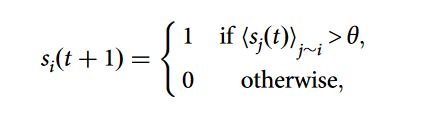
然而,现有研究相对忽视了从简单传染到复杂传染的过渡状态,没有人试图将实际的传染速度与这种过渡联系起来。这种传染速度,也被称为扩散速度,是单位时间内受感染的网络节点数量,并被越来越多的人认为是传染动态的一个重要指标。分析传染速度的一个指标是所谓的极化速度(Polarization speed)v = (P(t) - P(0))/t,其中P(t)是测量一个复杂网络系统在t时刻的极化程度。这个指标衡量了一个随机网络节点和它的邻居能够激活一定比例节点的速度,与平均扩散速度相同,也与传播速度等概念有一定关系。
在一个经典的小世界网络Watts-Strogatz(WS)中,研究者使用线性阈值模型模拟了从简单传染到复杂传染的过渡过程。研究者通过改变网络的平均最短路径 ℓ 、聚集系数 C 和基尔霍夫指数 Rg ,观察网络的极化速度和阈值。网络的平均最短路径定义为任意两个节点之间最短距离的平均值,聚集系数是表示一个网络中节点集聚程度的系数,而基尔霍夫指数又称有效电阻之和,能够基于网络的所有路径测量一个节点的重要程度以及网络的连通度(传播性能),基尔霍夫指数越小,节点间传播阻力越小,传播速度越快。以上三个指标能对网络拓结构实现有效衡量。
如图1所示,简单传染表现为在低阈值的情况下,极化速度随着网络平均最短路径和聚集系数的减小而加快。与之相反,在较高阈值的情况下,复杂传染的极化速度随着网络平均最短路径和聚集系数的增加而增加。正如预期的那样,过渡区域对应于阈值的中间值,因此不同网络的排序不会揭示明确的简单或复杂传染。
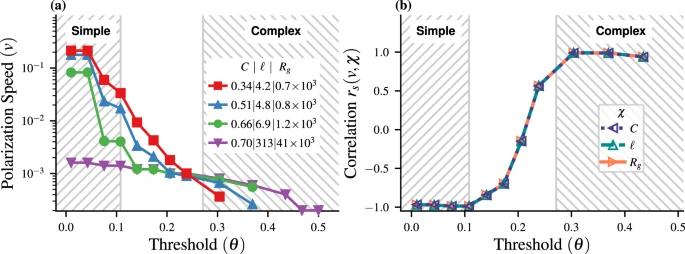
图1. 在N = 10, 000个节点的小世界网络上的线性阈值模型。(a)平均极化速度v 与阈值 θ 的关系。(b)极化速度 v 与每个网络属性 χ ∈ { C , ℓ , Rg } 的Spearman相关系数。
通过计算每个阈值下,极化速度v和每个网络指标χ∈{C,ℓ, Rg}之间的相关系数rs,阈值在0.1和0.28时rs≈+1,有一个明显的过渡(图1b)。这些阈值标志着纯粹的简单传染和复杂传染的分界线。值得注意,三个网络拓扑结构参数和极化速度之间的相关性极为相似,这是因为小世界网络模型只有一个自由参数。这些结果表明,描述传染动力学的极化速度 v 是行为传播性质(简单或复杂)的充分和有效指标。
2、从二元阈值模型到共识模型
通过经典的线性阈值模型,可以从一个新的角度来分析和理解从简单传染到复杂传染的过渡,即传染速度v。现在的问题是,这种过渡是否可以通过其他集体决策过程观察到?这些过程不涉及具有涌现变化的二元状态变量,也不涉及非线性机制/阈值。例如,鉴于鸟群和鱼群不断变化的集体动态,很少达成完全的行为共识,而通过二元模型向静止状态的收敛显然不能描述它们的动态。事实上,不断积累的经验证据表明,迅速的行为传播是集体行为的真正标志,而不是高度共识或极化。因此可以说,尽管共识是其集体行动的根源,但这些系统实际上倾向于脱离共识而运作。
那么,从简单传染到复杂传染的动态过程是否仍适用于共识模型这样的非二元集体决策过程呢?这项工作基于领导者-追随者共识模型来模拟基于共识的集体行为。在此模型中,主体(网络节点)通过对自己的状态和网络意义上的邻居的状态进行某种平均,来寻求达成共识。
通过给“领导者”(在某些情况下也被称为 "顽固"、"狂热"、"知情"的主体)强加一个特定的动力学,使系统偏离共识。领导者的行为传播到邻近的主体,并进一步传播到整个系统,从而决定出现的集体反应。然而,这种行为传播错综复杂地取决于网络拓扑结构,以及所考虑的领导者-追随者达成共识的频率(类似于上文的阈值θ)。系统的集体频率响应H2(ω)(类似于上文的极化速度v),可以解释为能够响应或跟随领导者行为的主体的数量,作为其频率 ω 的函数。
研究发现,在低频率(ω→0),集体响应H2(ω) 随着平均最短路径的减少而增加(图2a),类似于简单传染低阈值θ下极化速度 v 随平均最短路径的减小而增加。不足为奇的是,在低频下,观察到一种与简单传染相一致的现象。随着频率ω的增加,这一趋势被逆转,集体行为随着聚集系数的增加而增加,出现复杂传染。
然而,为了确定这种现象确实是从简单传染到复杂传染的过渡,必须验证低频时的简单传染是由平均最短路径或基尔霍夫指数驱动的,而高频的复杂传染则是由聚集系数驱动的。如图2b所示,对于这三个网络指标,相关系数表现出明显的正态趋势,与改变θ时观察到的阈值模型的趋势相呼应(图1b),而且中间有一个过渡区域。行为传播的有效性与聚集系数正相关,与基尔霍夫指数不相关,那么传染就很复杂。相反,如果一个行为传播与基尔霍夫指数负相关,与聚集系数不相关,那么它可以被归类为简单传染(图2c)。
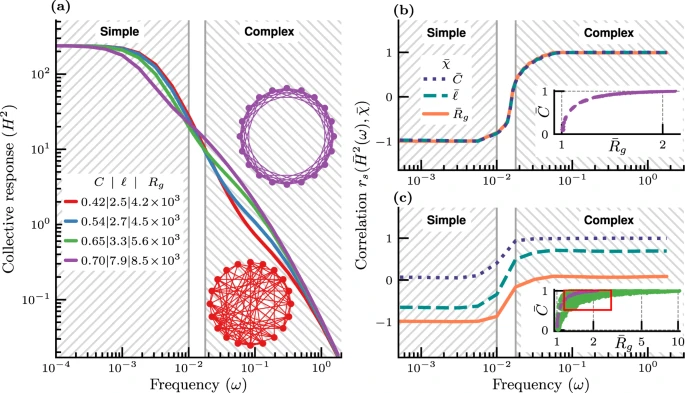
图2. N = 240 个节点的小世界网络上的领导者-追随者共识模型。
通过改变小世界网络的不同网络度数发现(图2c),在低频时,集体响应与基尔霍夫指数高度负相关,与聚集系数几乎不相关,而在高频率时情况则相反。这就明确地证实,在低频(或高频)下基于共识的行为传播是简单(或复杂)的传染类型。因此,无论是在基于二元阈值的集体行为,还是在没有任何阈值或非线性的分布式集体行为(基于共识)中, 以上结果再次证明,网络拓扑结构和传播速度影响了简单传染到复杂传染的过渡。
3、机器人网络中的复杂传染
为了使研究结论更具说服力,研究者还使用多机器人系统评估了在有非线性成分的集体决策的情况下,改变互动网络的拓扑结构时的各种社会传播行为。通过三种拓扑网络连接(Random、Ring、Caveman)的领导者-跟随者网络机器人系统的实验分析,结果确实与之前在更大网络中研究的复杂传染现象学非常一致(图3)。
在所考虑的所有三个网络,无论是机器实验还是模拟结果,集体响应的降低在低频下基本相同。而在中高频率ω ≤ 0.2范围内显示了丰富的集体行为,因为领导者的行为速度相当“快”,从而阻止了任何形式的方向共识的达成,这类似于处理快节奏扰动的动物群体的状态。
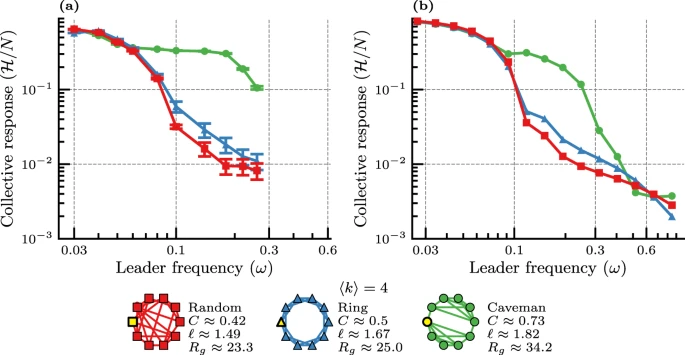
图3. 通过三种拓扑网络连接的领导者-跟随者网络机器人系统的实验分析结果。领导节点以黄色表示,(a)角度一致性动力学的实验结果;(b)非线性角度一致性动力学的模拟结果。
三、对舆论传播和疫情防控的现实启示
综上所述,此研究从理论上和实验上表明,复杂传染比原来想象的更为普遍,而且从简单到复杂传染并不限于基于阈值的模型(基于线性系统动力学),在一个没有任何阈值的完全线性行为决策(基于一种共识)中也发现了这一过渡,大大扩展了这一现象与社会科学以外的广大集体决策过程的相关性,包括集体动物行为和集群机器人。这项研究不仅可以为生物学家和社会科学家分别探索和实验动物和人类群体行为提供新的方向,也可以用于改进工程网络系统(例如,物联网、传感器网络、集群机器人)的设计和稳健性。此外,该项研究也能为当前的舆情管理和疫情防控提供借鉴。
传染的性质(简单或复杂)与传播行为的内在速度密切相关,网络拓扑强烈影响行为传播的有效性。通过模型能够确定与简单或复杂传染相关的控制参数的区间,并在两者之间有一个过渡区域。因此,通过控制过渡区间传染网络的拓扑结构或传播速度,就能引导/阻止简单传染向复杂传染的过渡。
以上结论启示我们在引导舆情和打击虚假信息时,只改变传播网络的拓扑结构,如删帖、控评和拉黑等,往往很难抑制传播行为的涌现,还需关注事件的传播速度。一个事件的传播速度往往与网民的偏好程度有关,对一个事件的“祛魅”(如沟通、辟谣和科普等)能够很好降低偏好程度,因为人类对“秘辛”的偏好远高于对事实的追求,这就是为什么在事件删贴后却能激起对此事件更大范围的传播,引发复杂传染。
同样道理,疫情的防控不仅要关注防控的精准性(对传播网络结构的精准识别和封控),更要关注不同变异毒株在传播速度上的差异。于德尔塔毒株爆发时期构建并成熟的精准防控经验,可能不适应传播速度更快的奥密克戎毒株,这可能是一些城市出现进退失据的原因。大城市能实现小区域的精准防控,而小城市在面临疫情时往往要封城应对,与不同城市可调用的资源以及应急响应系统的速度有关。在无法快速响应时(如快速的全域核酸检测、大规模医务人员的调度),在病毒传播速度不可控的情况下,全域封锁可能是大规模改变网络拓扑结构的无奈妥协。
标签:阈值,复杂,社交,网络,传播,传染,防控,涌现,行为 From: https://www.cnblogs.com/wangzheming35/p/16601465.html