哈哈,被干爆了。拖了cdqz哥后腿。
题目使用协议
来自 THUPC2024(2024年清华大学学生程序设计竞赛暨高校邀请赛)初赛。
以下『本仓库』皆指 THUPC2024 初赛 官方仓库
-
任何单位或个人都可以免费使用或转载本仓库的题目;
-
任何单位或个人在使用本仓库题目时,应做到无偿、公开,严禁使用这些题目盈利或给这些题目添加特殊权限;
-
如果条件允许,请在使用本仓库题目时同时提供数据、标程、题解等资源的获取方法;否则,请附上本仓库的 github 地址。
A. 排序大师
题目描述
由于你是排序大师,你经常被路过的游客***难,要求用一些奇怪的操作给序列排序。
由于你是远近闻名的排序大师,邻国的排序萌新小 I 慕名前来拜访,留下了一个长度为 \(n\) 的排列 \(a_1, a_2 \cdots, a_n\),并要求你用以下操作将排列升序排序:
- 定义 \(a_{i \sim j} = \{a_i,a_{i+1},\cdots, a_j\}\)。选定 \(1 \le i \le j < k \le l \le n\),交换 \(a_{i \sim j}\) 和 \(a_{k \sim l}\),即交换过后序列变为 \(a_{1 \sim i-1}, a_{k \sim l}, a_{j+1 \sim k-1}, a_{i \sim j}, a_{l+1 \sim n}\)。
由于你是因精益求精而远近闻名的排序大师,你需要给出一个排序方案最小化操作次数。
输入格式
输入的第一行一个整数 \(n(1 \le n \le 2,000)\) 表示序列长度,第二行 \(n\) 个整数 \(a_1,a_2,\cdots,a_n (1 \le a_i \le n)\) 描述排列。
输出格式
输出的第一行一个整数 \(s\) 表示你给出的方案的步数,接下来 \(s\) 行每行四个整数 \(i,j,k,l\) 表示一次操作。若有多个方案,输出任意一个即可。
样例
样例输入 #1
6
1 4 5 3 2 6
样例输出 #1
1
2 3 5 5
选定 \(i = 2, j = 3, k = 5, l = 5\),\(1 \textcolor{blue}{4 5} 3 \textcolor{red}{2} 6\) 变为 \(1 \textcolor{red}{2} 3 \textcolor{blue}{4 5} 6\)。
题解
笔者还不会。
B. 一棵树
题目描述
这里有一棵树,具体的,这是一张有 \(n\) 个节点和 \(n-1\) 条边组成的无向联通图。
每个节点初始颜色为白色,你需要恰好将其中 \(k\) 个节点染成黑色,定义一条边的权值是,断开这条边之后,两个连通块的黑色节点个数之差,定义一棵树的权值为所有边的权值求和,你需要最小化整棵树的权值。
输入格式
第一行两个正整数 \(n,k\)(\(1\leq k\leq n\leq 5\times10^5\))。
接下来 \(n-1\) 行,每行两个正整数 \(x,y\) 表示树上的一条边。
输出格式
输出共 \(1\) 行,表示最优的染色方案下,这棵树的权值的最小值。
样例
样例输入 #1
10 4
1 2
2 3
2 4
3 5
3 6
3 7
4 10
6 8
8 9
样例输出 #1
16
下图展示了一种满足条件的染色方案,边上的数字表示边权。
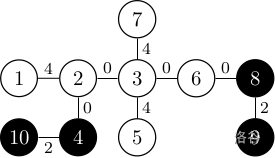
题解
容易想到一个平凡的树形dp:随便定一个根,设 \(f_{u,x}\) 表示以 \(u\) 为根的子树中选 \(x\) 个黑点,子树内部以及 \(u\) 与它父亲之间的边的代价和的最小值,于是有转移
\[f_{u,x}=|2x-k|+\min \left( \sum_{v \in son\left(u\right)} f_{v,y_v} \right),\ \sum_{v \in son\left( u \right)} y_v = x\nonumber \]一个经典结论是这样的背包合并不改变函数的凸性,因此 \(f_u\) 是一个下凸函数,对于转移后面的 \(\min\) 可以用合并差分序列的方式维护,前面的绝对值的差分为一段 \(-2\) 拼上一段 \(+2\),如果 \(k\) 是奇数的话还会有一个差分为 \(0\) 的点。
用两个可并堆维护这个差分序列:将整个单调不降的差分序列分成左右两部分,左边塞到大根堆,右边塞到小根堆,时刻保证左边大根堆的大小是 \(\lfloor \frac{k}{2} \rfloor\)(如果元素数量足够),那么这个分段的加法就可以变成对左边的大根堆整体 \(-2\),右边的小根堆整体 \(+2\)(当 \(k\) 是奇数的时候可能要先把一个点提出来),打tag即可维护,总时间复杂度 \(\mathcal{O}(n \log n)\)。
code for B
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10, M = 1e6 + 10;
int n, k, T, flag;
int h[N], e[M], ne[M], idx;
inline void add(int a, int b) {e[idx] = b, ne[idx] = h[a], h[a] = idx ++; }
struct node {
int lc, rc, siz, dist;
long long val, tag;
node() {lc = rc = siz = val = tag = 0, dist = -1; }
} A[N];
inline void Tag(int u, long long x) {if(u) A[u].tag += x, A[u].val += x; }
inline void pushdown(int u) {Tag(A[u].lc, A[u].tag), Tag(A[u].rc, A[u].tag), A[u].tag = 0; }
inline void maintain(int u) {if(u) A[u].siz = A[A[u].lc].siz + A[A[u].rc].siz + 1; }
struct Heap {
function<bool(long long, long long)> cmp;
int merge(int a, int b) {
if(!a || !b) return a + b;
if(cmp(A[b].val, A[a].val)) swap(a, b);
pushdown(a); A[a].rc = merge(A[a].rc, b);
if(A[A[a].lc].dist < A[A[a].rc].dist) swap(A[a].lc, A[a].rc);
A[a].dist = A[A[a].rc].dist + 1;
maintain(a); return a;
}
int remove(int &u) {
if(!u) return u;
pushdown(u); int x = u; u = merge(A[u].lc, A[u].rc);
A[x].lc = A[x].rc = A[x].dist = 0, A[x].siz = 1;
return x;
}
};
Heap L, R;
int idL[N], idR[N];
void dfs(int u, int fa) {
A[u].siz = 1, A[u].dist = 0, idL[u] = u;
for(int i = h[u]; i != -1; i = ne[i]) {
int v = e[i]; if(v == fa) continue;
dfs(v, u);
idL[u] = L.merge(idL[u], idL[v]);
idR[u] = R.merge(idR[u], idR[v]);
}
while(A[idL[u]].siz > T)
idR[u] = R.merge(idR[u], L.remove(idL[u]));
if(u == 1) return;
if(flag) {
Tag(idL[u], -2); int x = R.remove(idR[u]);
Tag(idR[u], 2), idR[u] = R.merge(x, idR[u]);
} else Tag(idL[u], -2), Tag(idR[u], 2);
}
int main() {
ios::sync_with_stdio(false), cin.tie(0);
memset(h, -1, sizeof h);
L.cmp = [](long long x, long long y) {return x > y; };
R.cmp = [](long long x, long long y) {return x < y; };
cin >> n >> k; T = k >> 1, flag = k & 1;
for(int i = 1; i < n; i ++) {
int a, b; cin >> a >> b;
add(a, b), add(b, a);
}
dfs(1, 0);
long long res = 1ll * (n - 1) * k;
assert(A[idL[1]].siz + A[idR[1]].siz >= k);
for(int i = 1; i <= k; i ++) {
if(idL[1]) res += A[idL[1]].val, L.remove(idL[1]);
else res += A[idR[1]].val, R.remove(idR[1]);
}
cout << res << '\n';
return 0;
}
C. 前缀和
题目描述
小兰很喜欢随机数。
TA 首先选定了一个实数 \(0 < p < 1\),然后生成了 \(n\) 个随机数 \(x_1,\dots,x_n\),每个数是独立按照如下方式生成的:
- \(x_i\) 有 \(p\) 的概率是 \(1\),有 \((1-p)p\) 的概率是 \(2\),有 \((1-p)^2p\) 的概率是 \(3\),以此类推。
生成完这些随机数之后,小艾对这个数列求了前缀和,得到了数列 \(y_1,\dots,y_n\)。
给定 \(1\leq l\leq r\leq n\),小兰想知道,期望有多少 \(y_i\) 落在 \([l, r]\) 内?
输入格式
一行输入四个数 \(n, p, l, r\)。保证 \(1\leq l\leq r\leq n\leq 10^9\),\(p\) 的位数不超过 \(6\)。
输出格式
输出一个实数,表示答案。你需要保证答案的绝对或相对误差不超过 \(10^{-6}\)。
样例
样例输入 #1
3 0.5 1 2
样例输出 #1
1.000000
有 \(1/4\) 的概率,\(x_1=1\) 而 \(x_2>1\),此时只有 \(y_1\) 落在 \([1, 2]\) 内。
有 \(1/4\) 的概率,\(x_1=1\) 且 \(x_2=1\),此时 \(y_1,y_2\) 落在 \([1, 2]\) 内。
有 \(1/4\) 的概率,\(x_1=2\),此时只有 \(y_1\) 落在 \([1, 2]\) 内。
所以期望是 \(1/4\cdot (1 + 2 + 1) = 1\)。
题解
先给一个std里的神秘双射做法:
考虑无穷个灯排成一排,每个灯有 \(p\) 的概率亮,有 \(1-p\) 的概率不亮,每个灯独立。
那么,\(x_1=a\) 的概率就是从左往右数,第一个亮着的灯是第 \(a\) 个灯的概率。因此又有,\(y_i=a\) 的概率就是从左往右数,第 \(i\) 个亮着的灯是第 \(a\) 个灯的概率,由此我们就成功构造出了一个双射。
在这个双射中,存在一个 \(y_i=a\) 就等价于第 \(a\) 个灯是亮着的,因此 \([l,r]\) 中亮着的灯的数量就等于在 \([l,r]\) 的 \(y_i\) 的数量,而每个灯亮的概率都是 \(p\),因此答案就是 \(p(r-l+1)\)。
上述神秘双射如果之前没有遇到过的话,很难在场上独自想出来当然可能是我太菜了,下面提供一个PGF常规推式子的经济实惠考场做法:
先写出来 \(x_i\) 的PGF是
\[F(z)=\sum_{i=0}^{+\infty}(1-p)^{i}p z^{i+1}\nonumber \]简单解一下这个GF:
\[\begin{align} &(1-p)z F(z)=\sum_{i=1}^{+\infty}(1-p)^{i}p z^{i+1}=F(z)-pz\nonumber\newline &\Longrightarrow F(z)=\frac{pz}{1-z+pz}\nonumber \end{align} \]那么 \(y_n\) 的PGF就是
\[\left( F(z) \right)^n\nonumber \]因为答案其实是
\[\sum_{i=1}^{n}P([l \le y_i \le r])\nonumber \]所以只需要提出来每个 \(y_i\) 的PGF在 \(z^{l..r}\) 处的系数和相加即可,由于 \(n \ge r\),因此将 \(n\) 看作 \(+\infty\) 是对答案无影响的,下面我们就这样做。
将所有 \(y_i\) 的PGF加起来:
\[\sum_{i=1}^{+\infty} \left( F(z) \right)^i=\frac{1}{1-F(z)}-1=\frac{1-z+pz}{1-z}-1=p\frac{z}{1-z}\nonumber \]一下子就得到了一个漂亮的式子,因为 \(1 \le l \le r \le n\),因此 \(\frac{z}{1-z}\) 在 \(l..r\) 项的系数都是 \(1\),所以答案就是 \(p(r-l+1)\),得到了和神秘双射相同的结果。
code for C
#include <bits/stdc++.h>
using namespace std;
int main() {
ios::sync_with_stdio(false), cin.tie(0);
int n, L, R; long double p;
cin >> n >> p >> L >> R;
cout << fixed << setprecision(6) << p * (R - L + 1) << '\n';
return 0;
}
D. 多折较差验证
题目描述
临海听潮意,入林闻籁鸣。这是一座依山傍水、宁静祥和的小镇,在这里人们很少担心自己家里的物品故障损坏,因为 Kanan 总能帮大家修好。Kanan 是这片地区首屈一指的机械师;虽然她还年轻,但是娴熟的技艺加上慷慨的性格使得她平时总会收到人们的修理委托,据说就连那位遗世独立的魔王遇到了问题都得求助她。在帮人修理时, Kanan 会接触到千奇百怪的使用说明书。其中一些说明书有着不可思议的折叠结构,Kanan 为了理解机械的构造会在修理之前展开说明书,可在修好之后按照原来的折痕折回原状却比修理本身更费劲。
对于所有折痕互相平行的说明书,可以按照说明书上文字的阅读顺序从上到下给每条折痕分别编号 \(1, 2, \cdots, N\),这 \(N\) 条折痕将说明书分成了 \((N+1)\) 条纸带。每条折痕可能为两种形态之一:一种是垂直纸面向内凸出,对应将纸的上下两半向前对折;一种是垂直纸面向外凸出,对应将上下两半向后对折。根据折痕截面的形状,分别使用小写字母 v 表示向内凸出的折痕,^ (ASCII 码为 \(94\))表示向外凸出的折痕。假设所有纸带的宽度都是一样的,并且折纸的过程中说明书不发生形变,那么沿着一条折痕对折后两侧的纸能够重合,当且仅当两侧的折痕是相反的;即,如果沿着第 \(k\) 条折痕折叠,那么对于所有满足 \(1\le k-m<k+m\le N\) 的正整数 \(m\),第 \((k-m)\) 条折痕和第 \((k+m)\) 条折痕的形态是相反的。例如,对于折痕依次为 v^v^^^^v 的说明书,可以沿其第 \(7\) 条折痕进行折叠。根据定义可知,一张说明书总能沿着第一条或最后一条折痕进行折叠。折叠之后的说明书可以用被折叠的折痕两侧中,剩余折痕数量较多一侧的折痕表示,如 v^v^^^^v 沿着第 \(7\) 条折痕折叠后得到 v^v^^^。如果被折叠的折痕两侧折痕数量相等,那么用哪一侧的折痕表示折叠后的纸都可以,因为折痕在三维空间中是旋转对称的。特别地,对只剩下一条折痕的说明书,即 v 或 ^ 进行折叠后,所有 \((N+1)\) 条纸带都重叠在一起,此时称这张说明书被折叠整齐。
虽然按顺序依次折叠每一条折痕,总能将说明书折叠整齐,但 Kanan 觉得这样并不美观。一种美观的折法应该尽量少折,并且每次折的时候折痕两侧应该尽可能的对称。定义一种折法的不对称程度为每次折叠时,被折叠的折痕两侧的折痕数量之差的总和。给出一张说明书的折痕,Kanan 想知道最少需要折多少次才能将这张说明书折叠整齐,以及所有折叠次数最少的折法中,不对称程度的最小值。
对于所有数据,保证 \(1\le N\le 5000\),\(|s|=N\) 且 \(s\) 仅由 v 和 ^ 组成。
输入格式
输入的第一行包含一个正整数 \(N\),表示折痕的条数。保证 \(1\le N\le 5000\)。
输入的第二行包含一个字符串 \(s\),按顺序表示每条折痕。保证 \(|s|=N\),且 \(s\) 仅由 v 和 ^ 组成。
输出格式
输出仅一行,包括两个非负整数,分别表示最少的折叠次数和最小化折叠次数的前提下的最小不对称程度,两个数之间用一个空格隔开。
样例
样例输入 #1
3
^vv
样例输出 #1
2 0
如果先沿着中间的折痕对折,那么两侧的纸恰好重合,此时再对折一次即可将说明书折叠整齐。
样例输入 #2
8
v^v^^^^v
样例输出 #2
6 15
样例输入 #3
40
v^vv^v^^v^^vvvv^v^^v^^^vv^^vvvv^v^^v^^^v
样例输出 #3
14 201
样例输入 #4
56
v^vvvvvvv^v^^vv^v^^v^^^^v^^v^vvvv^^vvvv^v^^v^^^vv^^vv^v^
样例输出 #4
24 663
题解
一个显然的想法是区间dp,只需要 \(\mathcal{O}(n^2)\) 预处理一下每个位置可以折的最大半径即可,总复杂度 \(\mathcal{O}(n^3)\) 肯定过不了。
注意力集中一点就可以注意到极大半径和不会很大,因此我们在区间dp枚举转移点的时候,不要从左端点到右端点扫过去,而是直接找覆盖了左端点或右端点的位置转移,复杂度大概是 \(\mathcal{O(n^2 \log n)}\) 的,但是出题人和验题人和我都不会证。
code for D
#include <bits/stdc++.h>
using namespace std;
const int N = 5010;
int n; char S[N];
int R[N]; vector<int> cover[2][N];
pair<int, int> f[N][N];
int main() {
ios::sync_with_stdio(false), cin.tie(0);
cin >> n >> (S + 1);
for(int i = 1; i <= n; i ++) {
R[i] = 0;
while(i - R[i] > 1 && i + R[i] < n && S[i - R[i] - 1] != S[i + R[i] + 1])
R[i] ++;
}
for(int i = 1; i <= n; i ++)
cerr << R[i] << " \n"[i == n];
for(int i = 1; i <= n; i ++)
for(int j = 0; j <= R[i]; j ++)
cover[0][i - j].emplace_back(i), cover[1][i + j].emplace_back(i);
for(int i = 1; i <= n; i ++)
reverse(cover[1][i].begin(), cover[1][i].end());
for(int i = 1; i <= n; i ++) f[i][i] = {1, 0};
for(int len = 2; len <= n; len ++) for(int l = 1; l + len - 1 <= n; l ++) {
int r = l + len - 1; f[l][r] = {n + 1, 0};
int mid = (l + r) >> 1;
for(auto x : cover[0][l]) {
if(x > mid) break; int y = (r - x) - (x - l);
f[l][r] = min(f[l][r], {f[x + 1][r].first + 1, f[x + 1][r].second + y});
}
for(auto x : cover[1][r]) {
if(x <= mid) break; int y = (x - l) - (r - x);
f[l][r] = min(f[l][r], {f[l][x - 1].first + 1, f[l][x - 1].second + y});
}
}
cout << f[1][n].first << ' ' << f[1][n].second << '\n';
return 0;
}
E. 转化
题目描述
小 E 在玩 Somzig 游戏的时候因为操作时间不够绷不住了,于是就有了这个题。
小 E 有 \(n\) 种颜色的球,其中第 \(i\) 种有 \(a_i\) 个。有两类工具,第一类可以把一个指定颜色的球变成一个任意颜色的球;第二类可以把一个指定颜色的球变成两个这种颜色的球。一个变化之后的球也可以通过工具产生新的变化。关于第 \(i\) 种颜色的第一类工具有 \(b_i\) 个,第二类工具有 \(c_i\) 个。小 E 想知道,如果每一个工具最多只能使用一次,那么对于每种颜色 \(i\),第 \(i\) 种颜色的球最后最多能有多少个。以及,小 E 最后最多能有多少个球。
输入格式
第一行一个正整数 \(n\)。
第二行 \(n\) 个整数,其中第 \(i\) 个表示 \(a_i\)。
第三行 \(n\) 个整数,其中第 \(i\) 个表示 \(b_i\)。
第四行 \(n\) 个整数,其中第 \(i\) 个表示 \(c_i\)。
输出格式
第一行 \(n\) 个整数,其中第 \(i\) 个表示如果每个工具最多使用一次,那么小 E 最后第 \(i\) 种颜色的球最多有多少个。
第二行一个整数,表示如果每个工具最多使用一次,那么小 E 最后最多能有多少个球。
保证 \(1\le n \le 351493\)。
保证 \(0\le a_i,b_i,c_i\le 10^9\)。
样例
样例输入 #1
2
1 2
1 2
1 0
样例输出 #1
4 3
4
题解
对于每个颜色,我们可以用 \(x+1\) 个工具一加上 \(x\) 个工具二将一个该颜色球变为 \(x+1\) 个任意颜色球。
对于 \(A_i \ne 0\),我们可以将它转换为 \(\min\left( A_i+C_i,B_i \right)\) 个任意颜色的球,对于 \(A_i=0\),我们只需要一个之前得到的任意颜色的球就可以免费多拿 \(\max\left(0, \min\left( 1+C_i,B_i \right)-1 \right)\) 个任意颜色的球。
因此对于第一问,先扫一遍所有颜色的球,算出来可以拿多少任意颜色的球以及付出一个任意颜色球的代价可以再多拿多少任意颜色的球,对于每种颜色的询问,先把这个颜色的贡献扣掉,答案就是这种颜色的球的数量加上可以免费拿到的球的数量,时间复杂度 \(\mathcal{O}(n)\)。
对于第二问,先将 \(A_i \ne 0\) 的工具二用上,假如有任意颜色的球,将免费得到的算上,最后还有 \(A_i=0,B_i=0\) 的球,将这些球按照 \(C_i\) 降序排,贪心地选即可,时间复杂度 \(\mathcal{O}(n \log n)\),瓶颈在排序。
code for E
#include <bits/stdc++.h>
using namespace std;
const int N = 4e5 + 10;
int n, A[N], B[N], C[N];
int main() {
ios::sync_with_stdio(false), cin.tie(0);
cin >> n;
for(int i = 1; i <= n; i ++) cin >> A[i];
for(int i = 1; i <= n; i ++) cin >> B[i];
for(int i = 1; i <= n; i ++) cin >> C[i];
long long offer = 0, add = 0;
{
for(int i = 1; i <= n; i ++) {
if(A[i] == 0)
add += max(0, min(C[i] + 1, B[i]) - 1);
else offer += min(A[i] + C[i], B[i]);
}
for(int i = 1; i <= n; i ++) {
long long ini = offer, now = add, self = 0;
if(A[i])
ini -= min(A[i] + C[i], B[i]), self += A[i] + C[i];
else
now -= max(0, min(C[i] + 1, B[i]) - 1), now += C[i];
if(offer) self += ini + now;
cout << self << " \n"[i == n];
}
}
{
long long res = 0; vector<long long> vec;
for(int i = 1; i <= n; i ++) {
if(A[i] != 0)
res += A[i] + C[i];
else if(B[i] && offer)
offer += min(C[i], B[i] - 1), res += C[i];
else vec.emplace_back(C[i]);
}
sort(vec.begin(), vec.end(), greater<long long> ());
for(int i = 0; i < vec.size() && i < offer; i ++)
res += vec[i];
cout << res << '\n';
}
return 0;
}
F. 机器人
题目描述
有 \(n\) 个机器人围成一圈,编号按照逆时针顺序分别为 \(0\sim n-1\)。
每个机器人有两只手。编号为 \(i\) 的机器人初始「左手」指向编号 \(l_i\) 的机器人,「右手」指向编号 \(r_i\) 的机器人。
所有的机器人内部都写有 \(m\) 行「指令」,「指令」有以下这些形式:
指令
「指令」分为「基础指令」和「高级指令」两种。「高级指令」的功能会更复杂一些,但它们本质上没有多大区别。下面介绍这些「指令」的格式以及它们被「执行」时的效果。文中的“自己”一词均指拥有这条「指令」的机器人。
基础指令
SLACKOFF:「摸鱼」,即什么也不做。MOVE h z:将第 \(h\) 只手向逆时针方向「移动」\(z\) 个机器人的位置。当 \(h=0\) 时表示「左手」,当 \(h=1\) 时表示「右手」,下同。SWAP h x y:将第 \(h\) 只手指向的机器人的第 \(x\) 行「指令」与自己的第 \(y\) 行「指令」「对调」。MIRROR h x:将第 \(h\) 只手指向的机器人的第 \(x\) 行「指令」「镜像」取反,即将「指令」中的 \(h\) 取反(\(0\) 变成 \(1\),\(1\) 变成 \(0\))。特殊地,它对SLACKOFF指令没有效果;而对TRIGGER指令,会直接修改「触发」时「执行」的「指令」中的 \(h\)。REPLACE h x <COMMAND>:将第 \(h\) 只手指向的机器人的第 \(x\) 行「指令」「替换」为<COMMAND>。其中<COMMAND>为一条完整的「指令」。
高级指令
-
ACTIVATE h:「激活」第 \(h\) 只手指向的机器人,即按顺序「执行」那个机器人的所有「指令」。前一行「指令」「执行」完毕之后才会「执行」后一行。注意在「执行」前面的「指令」时后面的「指令」可能会发生更改,这时需要「执行」更改后的「指令」。当那个机器人的所有「指令」「执行」完毕后,该「指令」才算「执行」完毕。 -
TRIGGER <COMMANDNAME>: <COMMAND>:其中<COMMANDNAME>表示「指令」的名称,即一条「指令」中的第一个全大写单词;<COMMAND>表示一条完整的「基础指令」。TRIGGER指令不会被「执行」,即按顺序「执行」时会跳过该「指令」。但是,当一个其他机器人「执行」完一条「指令」之后,且「右手」指向自己的时候,自己最靠前的满足如下条件的TRIGGER指令(如果有)就会被「触发」——「执行」一次对应的<COMMAND>:<COMMANDNAME>不为TRIGGER时,刚刚「执行」完毕的「指令」为<COMMANDNAME>指令;<COMMANDNAME>为TRIGGER时,刚刚「执行」完毕的「指令」是TRIGGER指令被「触发」时「执行」的「指令」。
「执行」完毕后会回到原来的「执行」顺序中。
你需要从 \(0\) 号机器人开始按照编号顺序一圈又一圈地「激活」这些机器人,并输出「执行」的前 \(k\) 条指令的有关信息。
第一行三个正整数 \(n,m,k\)。
接下来按照编号从小到大的顺序表示 \(n\) 个机器人的信息。
对于每个机器人,第一行两个非负整数 \(l_i,r_i\) 表示「左手」指向的机器人编号和「右手」指向的机器人编号。
接下来 \(m\) 行,按顺序表示机器人的「指令」,「指令」的格式见题目描述。
输出 \(k\) 行,按顺序描述前 \(k\) 条开始「执行」的指令的相关信息,在开始「执行」前输出,每条一行,格式如下:
- 「摸鱼」时输出
Robot <id> slacks off.。其中<id>为一个整数,表示「执行」当前「指令」的机器人编号,下同。 - 「移动」时输出
Robot <id> moves its <side> hand towards Robot <id2>.。其中<side>为left或right,表示移动了哪只手(left表示「左手」,right表示「右手」);<id2>为一个整数,表示移动之后这只手指向的机器人的编号。 - 「对调」时输出
Robot <id> swaps a line of command with Robot <id2>.。其中<id2>为一个整数,表示与之「对调」「指令」的机器人编号。 - 「镜像」取反时输出
Robot <id> modifies a line of command of Robot <id2>.。其中<id2>为一个整数,表示被「镜像」取反「指令」的机器人编号。 - 「替换」时输出
Robot <id> replaces a line of command of Robot <id2>.。其中<id2>为一个整数,表示被「替换」「指令」的机器人编号。 - 「执行」
ACTIVATE指令「激活」(区别于你的一圈又一圈的「激活」)时输出Robot <id> activates Robot <id2>.。其中<id2>为一个整数,表示被「激活」的机器人编号。 TRIGGER指令由于不会被「执行」就不需要输出,但当它们被「触发」时,仍然需要按照上面的格式输出对应的「基础指令」被「执行」的信息。
样例
样例输入 #1
2 2 5
0 0
MOVE 1 1
MOVE 0 1
0 1
TRIGGER MOVE: MOVE 0 1
SLACKOFF
样例输出 #1
Robot 0 moves its right hand towards Robot 1.
Robot 1 moves its left hand towards Robot 1.
Robot 0 moves its left hand towards Robot 1.
Robot 1 moves its left hand towards Robot 0.
Robot 1 slacks off.
TRIGGER 指令的「触发」时机是「执行」完毕之后。注意不能「触发」自己的 TRIGGER 指令。
样例输入 #2
2 2 4
0 1
ACTIVATE 1
SLACKOFF
0 1
SWAP 0 2 2
MIRROR 0 1
样例输出 #2
Robot 0 activates Robot 1.
Robot 1 swaps a line of command with Robot 0.
Robot 1 slacks off.
Robot 0 modifies a line of command of Robot 0.
注意在「执行」前面的「指令」时后面的「指令」可能会发生更改,这时需要「执行」更改后的「指令」。
样例输入 #3
3 2 6
1 2
ACTIVATE 0
ACTIVATE 0
2 1
SWAP 0 2 2
TRIGGER ACTIVATE: REPLACE 0 2 SLACKOFF
0 1
TRIGGER MIRROR: SLACKOFF
SLACKOFF
样例输出 #3
Robot 0 activates Robot 1.
Robot 1 swaps a line of command with Robot 2.
Robot 1 slacks off.
Robot 2 replaces a line of command of Robot 0.
Robot 0 slacks off.
Robot 1 swaps a line of command with Robot 2.
ACTIVATE 指令「激活」另一个机器人时,当那个机器人的所有「指令」「执行」完毕后,该「指令」才算「执行」完毕。
样例输入 #4
3 2 8
0 1
SLACKOFF
TRIGGER MOVE: SLACKOFF
1 2
TRIGGER TRIGGER: SLACKOFF
TRIGGER SLACKOFF: MOVE 0 1
2 0
TRIGGER SLACKOFF: MOVE 1 2
TRIGGER TRIGGER: MOVE 1 1
样例输出 #4
Robot 0 slacks off.
Robot 1 moves its left hand towards Robot 2.
Robot 2 moves its right hand towards Robot 1.
Robot 1 slacks off.
Robot 2 moves its right hand towards Robot 0.
Robot 0 slacks off.
Robot 1 slacks off.
Robot 2 moves its right hand towards Robot 2.
只有自己最靠前的满足条件的 TRIGGER 指令才会被 「触发」。
样例输入 #5
见附加文件的 5.in
样例输出 #5
见附加文件的 5.ans
无私的馈赠?有力的援助?
保证所有的指令的格式均正确。
保证输入文件的长度不超过 \(5\mathtt{MB}\)。
保证能够「执行」至少 \(k\) 条「指令」。
保证 \(2\le n\le 100\),\(1\le m \le 10\),\(1\le k \le 3\times 10^5\)。
保证 \(0\le l_i,r_i<n\)。
保证 \(0\le h \le 1\),\(1\le x,y \le m\),\(1\le z<n\)。所有输入的数都是整数。
题解
模拟题,注意不要每次拷贝的时候都拷整个命令,而是拷一下命令的指针即可。
如果在第51个点TLE,注意当某一个命令是一堆REPLACE套起来,将自己的这个指令脱下去一层的话,时间复杂度是 \(\mathcal{O}(nmk)\) 的,会被1s的时限卡掉。笔者的解决方法是判断一下每个机器人,假如它全是TRIGGER命令就跳过,这个时候这个特殊数据的复杂度就是 \(\mathcal{O}(k(n+m))\) 了。
code for F
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int n, m, k;
int siz_TRIGGER[N];
inline void Plus(int &a, int b) {assert(b >= 1 && b < n); a += b; if(a >= n) a -= n;}
enum {SLACKOFF, MOVE, SWAP, MIRROR, REPLACE, ACTIVATE, TRIGGER};
inline int F(string str) {
if(str == "SLACKOFF") return SLACKOFF;
if(str == "MOVE") return MOVE;
if(str == "SWAP") return SWAP;
if(str == "MIRROR") return MIRROR;
if(str == "REPLACE") return REPLACE;
if(str == "ACTIVATE") return ACTIVATE;
if(str == "TRIGGER") return TRIGGER;
assert(false);
}
struct command {
int type;
int h, x, y, z;
int T; command *p;
inline void copy(command *cp) {
type = cp->type, h = cp->h, x = cp->x, y = cp->y, z = cp->z;
T = cp->T, p = cp->p;
}
inline void input() {
string str; cin >> str; type = F(str);
if(type == SLACKOFF) return;
else if(type == MOVE) scanf("%d%d", &h, &z);
else if(type == SWAP) scanf("%d%d%d", &h, &x, &y);
else if(type == MIRROR) scanf("%d%d", &h, &x);
else if(type == REPLACE) scanf("%d%d", &h, &x), p = new command(), p->input();
else if(type == ACTIVATE) scanf("%d", &h);
else {
cin >> str; str.pop_back(); T = F(str);
p = new command(); p->input();
}
}
};
struct robot {
int id, l, r;
command *C[11];
inline void input(int _id) {
id = _id; cin >> l >> r;
for(int i = 1; i <= m; i ++)
C[i] = new command(), C[i]->input(), siz_TRIGGER[id] += C[i]->type == TRIGGER;
}
};
robot *A[N];
inline int& hand(robot *p, int h) {return !h ? p->l : p->r; }
void Activate(robot *p);
void Activate(robot *bot, command *p, bool normal);
int tot = 0;
void Activate(robot *p) {
for(int i = 1; i <= m; i ++)
Activate(p, p->C[i], true);
}
inline void Slackoff(robot *p) {
printf("Robot %d slacks off.\n", p->id);
if(++tot == k) exit(0);
}
inline void Move(robot *p, int h, int z) {
Plus(hand(p, h), z);
printf("Robot %d moves its %s hand towards Robot %d.\n", p->id, !h ? "left" : "right", hand(p, h));
if(++tot == k) exit(0);
}
inline void Swap(robot *p, int h, int x, int y) {
siz_TRIGGER[hand(p, h)] -= A[hand(p, h)]->C[x]->type == TRIGGER;
siz_TRIGGER[p->id] -= p->C[y]->type == TRIGGER;
swap(A[hand(p, h)]->C[x], p->C[y]);
siz_TRIGGER[hand(p, h)] += A[hand(p, h)]->C[x]->type == TRIGGER;
siz_TRIGGER[p->id] += p->C[y]->type == TRIGGER;
printf("Robot %d swaps a line of command with Robot %d.\n", p->id, hand(p, h));
if(++tot == k) exit(0);
}
inline void Mirror(robot *p, int h, int x) {
if(A[hand(p, h)]->C[x]->type != TRIGGER) {
command* tmp = new command(); tmp->copy(A[hand(p, h)]->C[x]);
A[hand(p, h)]->C[x] = tmp, A[hand(p, h)]->C[x]->h ^= 1;
} else {
command* tmp = new command(); tmp->copy(A[hand(p, h)]->C[x]->p);
A[hand(p, h)]->C[x]->p = tmp;
A[hand(p, h)]->C[x]->p->h ^= 1;
}
printf("Robot %d modifies a line of command of Robot %d.\n", p->id, hand(p, h));
if(++tot == k) exit(0);
}
inline void Replace(robot *p, int h, int x, command *C) {
siz_TRIGGER[hand(p, h)] -= A[hand(p, h)]->C[x]->type == TRIGGER;
A[hand(p, h)]->C[x]->copy(C);
siz_TRIGGER[hand(p, h)] += A[hand(p, h)]->C[x]->type == TRIGGER;
printf("Robot %d replaces a line of command of Robot %d.\n", p->id, hand(p, h));
if(++tot == k) exit(0);
}
inline void check_TRIGGER(robot *p, bool normal, int lst) {
for(int i = 1; i <= m; i ++) if(p->C[i]->type == TRIGGER) {
if((p->C[i]->T == TRIGGER && !normal) || (p->C[i]->T == lst)) {
Activate(p, p->C[i]->p, false);
break;
}
}
}
void Activate(robot *bot, command *P, bool normal = true) {
command* p = new command(); p->copy(P);
if(p->type == SLACKOFF) Slackoff(bot);
else if(p->type == MOVE) Move(bot, p->h, p->z);
else if(p->type == SWAP) Swap(bot, p->h, p->x, p->y);
else if(p->type == MIRROR) Mirror(bot, p->h, p->x);
else if(p->type == REPLACE) Replace(bot, p->h, p->x, p->p);
else if(p->type == ACTIVATE) {
printf("Robot %d activates Robot %d.\n", bot->id, hand(bot, p->h));
if(++tot == k) exit(0);
Activate(A[hand(bot, p->h)]);
} else assert(p->type == TRIGGER);
if(p->type != TRIGGER && bot->r != bot->id)
check_TRIGGER(A[bot->r], normal, p->type);
delete p;
}
int main() {
scanf("%d%d%d", &n, &m, &k);
for(int i = 0; i < n; i ++)
A[i] = new robot(), A[i]->input(i);
while(true) {
for(int i = 0; i < n; i ++)
if(siz_TRIGGER[i] != m) Activate(A[i]);
}
return 0;
}
G. 采矿
题目描述
“我已经买不起第二个机器人了。”
“那就雇点人来凑数吧。注意别给死里头。”
你是一个矿坑老板。
你的矿坑是二叉树形结构,有 \(n\) 个节点。\(1\) 号点为地面,对于所有的 \(2\le i\le n\),\(i\) 号节点与更浅层的 \(f_i\) 号节点通过通道相连,其中 \(f_i<i\),且相同的 \(f_i\) 最多出现两次。矿坑的不同节点的产量和开采难度均不相同。对于 \(i\) 号节点 \((2\le i\le n)\),如果派一个机器人开采,一单位时间内能有 \(r_i\) 的产出;如果派一个人类开采,一单位时间内能有 \(p_i\) 的产出。地面没有产出。
你有一个机器人,初始位于 \(s\) 号节点。你的矿坑里初始没有人类工人。
所有通道与节点都十分狭窄,每个节点都只能容下一名工人(工人包括人类和机器人),每个通道也只能恰好容一名工人通过。在移动的任何时刻,只能有最多一名工人在通道中,其余工人都必须在节点上。
你现在有 \(q\) 条计划需要按顺序执行。每个计划分为准备、执行、调整、开采四个阶段。
在准备阶段,人类可以在满足上述移动规则的前提下任意移动,但不能进入或离开矿坑(矿坑内的工人到达 \(1\) 号节点不算离开矿坑),因为你在看着他们;移动的顺序和次数均没有限制。机器人不能移动。
在执行阶段,不同计划需要做的事情可能不同,共分为 \(4\) 种:
- 机器人只能沿通道向更浅的方向移动,且至少需要经过一条通道。人类不能移动。
- 机器人只能沿通道向更深的方向移动,且至少需要经过一条通道。人类不能移动。
- 使一名人类从 \(1\) 号节点进入矿坑(这意味着该阶段开始时 \(1\) 号节点上必须没有工人)。除此之外所有工人都不能移动。
- 使一名人类从 \(1\) 号节点移出矿坑(这意味着该阶段开始时 \(1\) 号节点上必须有一名人类)。除此之外所有工人都不能移动。
在调整阶段,限制与准备阶段相同。人类可以在满足上述移动规则的前提下任意移动,但不能进入或离开矿坑;移动的顺序和次数均没有限制。机器人不能移动。
在开采阶段,所有的工人会采一单位时间的矿。所有有工人的非地面节点会根据位于该节点的工人种类计算产出。没有工人的节点没有产出。该计划的产出为所有节点的产出之和。
问按顺序执行完所有计划之后,你所有计划的产出之和最多可以达到多少。
输入格式
第一行三个正整数 \(n,q,s\)。
第二行 \(n-1\) 个整数,其中第 \(i\)(\(1\le i<n\),下同)个表示 \(f_{i+1}\)。
第三行 \(n-1\) 个整数,其中第 \(i\) 个表示 \(r_{i+1}\)。
第四行 \(n-1\) 个整数,其中第 \(i\) 个表示 \(p_{i+1}\)。
接下来 \(q\) 行,每行一个整数表示计划的种类,其中第 \(i\) 个整数表示第 \(i\) 条计划:
1表示第一种计划:将机器人向更浅的方向移动;2表示第二种计划:将机器人向更深的方向移动;3表示第三种计划:将一名人类从 \(1\) 号节点送入矿坑;4表示第四种计划:将一名人类从 \(1\) 号节点移出矿坑。
输出格式
如果无论如何你都无法完成你的计划,输出一行 No solution.。否则输出一行一个整数,表示你的产出之和的最大值。
样例
样例输入 #1
5 6 4
1 1 3 3
15 9 7 1
4 2 8 6
3
3
1
2
2
4
样例输出 #1
91
一个最优解如下:(一些没有移动的阶段略过不提)
第一个计划的调整阶段:将刚送入 \(1\) 号点的人类移动两次到 \(5\) 号点。
第一个计划的开采阶段:机器人产出为 \(7\),人类产出为 \(6\)。
第二个计划的调整阶段:将刚送入 \(1\) 号点的人类移动到 \(2\) 号点。
第二个计划的开采阶段:机器人产出为 \(7\),人类产出为 \(4+6=10\)。
第三个计划的执行阶段:将机器人移动至 \(1\) 号点。
第三个计划的调整阶段:将一名人类从 \(5\) 号点移动至 \(4\) 号点。
第三个计划的开采阶段:机器人产出为 \(0\),人类产出为 \(4+8=12\)。
第四个计划的准备阶段:将一名人类从 \(4\) 号点移动至 \(5\) 号点。
第四个计划的执行阶段:将机器人移动至 \(3\) 号点。
第四个计划的开采阶段:机器人产出为 \(9\),人类产出为 \(4+6=10\)。
第五个计划的执行阶段:将机器人移动至 \(4\) 号点。
第五个计划的开采阶段:机器人产出为 \(7\),人类产出为 \(4+6=10\)。
第六个计划的准备阶段:将一名人类从 \(2\) 号点移动至 \(1\) 号点。
第六个计划的开采阶段:机器人产出为 \(7\),人类产出为 \(6\)。
总的产出为 \(7+6+7+10+0+12+9+10+7+10+7+6=91\)。
数据范围
保证 \(2\le n\le 301\),\(1\le q \le 600\),\(1\le s\le n\)。
保证 \(1\le f_i < i\),\(0\le r_i,p_i \le 10^9\)。
保证相同的 \(f_i\) 最多出现两次。
题解
注意到机器人只会有一个,而我们只关心机器人所在的位置以及i机器人将整个二叉树分成的每个联通块中有几个工人(某个联通块中工人的具体位置我们并不关心,因为在两次执行之间总可以随意变化)。
于是就有dp,设 \(dp_{u,i,j}\) 表示当前机器人在点 \(u\),\(u\) 的左子树中有 \(i\) 个工人,右子树中有 \(j\) 个工人的最大答案。
因为每个时刻工人总数是知道的,因此外子树(整棵树删掉 \(u\) 的子树)中工人的数量也是知道的。
状态总数是每个点的两棵子树大小的乘积,为 \(\mathcal{O}(n^2)\),每次直接暴力转移,预处理一个每个子树、外子树内有 \(x\) 个工人时一次开采可以获得的最大价值就可以做到单次转移 \(\mathcal{O}(n^2)\),滚动数组优化空间,总时间复杂度 \(\mathcal{O}(qn^2)\),可以通过.
code for G
#include <bits/stdc++.h>
using namespace std;
const int N = 305;
const long long INF = 0x3f3f3f3f3f3f3f3fLL;
int n, q, s, fa[N], siz[N], ch[N][2], p[N], r[N];
vector<long long> in[N], out[N];
int begin_dfn[N], end_dfn[N], dfs_clock;
void init_dfs(int u) {
begin_dfn[u] = ++dfs_clock;
if(ch[u][0]) init_dfs(ch[u][0]);
if(ch[u][1]) init_dfs(ch[u][1]);
end_dfn[u] = dfs_clock;
}
inline bool in_sub_tree(int v, int u) {return begin_dfn[u] <= begin_dfn[v] && begin_dfn[v] <= end_dfn[u]; }
int cur = 0, human_number = 0;
vector<vector<long long>> dp[2][N];
long long L[N], R[N];
void up_dfs(int u) {
if(ch[u][0]) up_dfs(ch[u][0]);
if(ch[u][1]) up_dfs(ch[u][1]);
for(int i = 0; i <= siz[ch[u][0]]; i ++) L[i] = -INF;
for(int i = 0; i <= siz[ch[u][1]]; i ++) R[i] = -INF;
static auto calc = [&](int x, long long A[]) {
for(int i = 0; i <= siz[ch[x][0]]; i ++)
for(int j = 0; j <= siz[ch[x][1]]; j ++)
A[i + j] = max(A[i + j], max(dp[cur ^ 1][x][i][j], dp[cur][x][i][j]));
};
if(ch[u][0]) calc(ch[u][0], L);
if(ch[u][1]) calc(ch[u][1], R);
for(int i = 0; i <= siz[ch[u][0]]; i ++)
for(int j = 0; j <= siz[ch[u][1]]; j ++)
if(i + j <= human_number && human_number - i - j <= n - siz[u])
dp[cur][u][i][j] = max(dp[cur][u][i][j], max(L[i], R[j]));
}
void down_dfs(int u) {
if(ch[u][0]) {
int x = ch[u][0];
for(int i = 0; i <= siz[x]; i ++) L[i] = -INF;
for(int i = 0; i <= siz[x]; i ++)
for(int j = 0; j <= siz[ch[u][1]]; j ++)
L[i] = max(L[i], max(dp[cur ^ 1][u][i][j], dp[cur][u][i][j]));
for(int i = 0; i <= siz[ch[x][0]]; i ++)
for(int j = 0; j <= siz[ch[x][1]]; j ++)
dp[cur][x][i][j] = max(dp[cur][x][i][j], L[i + j]);
}
if(ch[u][1]) {
int x = ch[u][1];
for(int i = 0; i <= siz[x]; i ++) R[i] = -INF;
for(int i = 0; i <= siz[ch[u][0]]; i ++)
for(int j = 0; j <= siz[x]; j ++)
R[j] = max(R[j], max(dp[cur ^ 1][u][i][j], dp[cur][u][i][j]));
for(int i = 0; i <= siz[ch[x][0]]; i ++)
for(int j = 0; j <= siz[ch[x][1]]; j ++)
dp[cur][x][i][j] = max(dp[cur][x][i][j], R[i + j]);
}
if(ch[u][0]) down_dfs(ch[u][0]);
if(ch[u][1]) down_dfs(ch[u][1]);
}
void add_human() {
human_number ++;
for(int u = 1; u <= n; u ++)
for(int i = 0; i <= siz[ch[u][0]]; i ++)
for(int j = 0; j <= siz[ch[u][1]]; j ++)
if(dp[cur ^ 1][u][i][j] != -INF && n - siz[u] >= human_number - i - j)
dp[cur][u][i][j] = dp[cur ^ 1][u][i][j];
}
void erase_human() {
human_number --;
for(int u = 1; u <= n; u ++)
for(int i = 0; i <= siz[ch[u][0]]; i ++)
for(int j = 0; j <= siz[ch[u][1]]; j ++)
if(dp[cur ^ 1][u][i][j] != -INF && human_number - i - j >= 0)
dp[cur][u][i][j] = dp[cur ^ 1][u][i][j];
}
int main() {
ios::sync_with_stdio(false), cin.tie(0);
cin >> n >> q >> s;
for(int i = 2; i <= n; i ++) cin >> fa[i];
for(int i = 2; i <= n; i ++) cin >> r[i];
for(int i = 2; i <= n; i ++) cin >> p[i];
for(int i = 2; i <= n; i ++)
ch[fa[i]][!ch[fa[i]][0] ? 0 : 1] = i;
for(int i = n; i >= 1; i --)
siz[i] = siz[ch[i][0]] + siz[ch[i][1]] + 1;
vector<int> vec(n); iota(vec.begin(), vec.end(), 1);
sort(vec.begin(), vec.end(), [&](int x, int y) {return p[x] > p[y]; });
init_dfs(1);
for(int u = 1; u <= n; u ++) {
in[u].emplace_back(0), out[u].emplace_back(0);
for(auto v : vec) {
if(in_sub_tree(v, u)) in[u].emplace_back(in[u].back() + p[v]);
else out[u].emplace_back(out[u].back() + p[v]);
}
assert(in[u].size() == siz[u] + 1);
assert(out[u].size() == n - siz[u] + 1);
}
in[0].resize(n + 1, 0), out[0].resize(n + 1, 0);
for(int i = 0; i <= 1; i ++)
for(int u = 1; u <= n; u ++)
dp[i][u].resize(siz[ch[u][0]] + 1, vector<long long>(siz[ch[u][1]] + 1, -INF));
dp[cur][s][0][0] = 0;
while(q --) {
cur ^= 1;
int type; cin >> type;
for(int u = 1; u <= n; u ++)
for(auto &vec : dp[cur][u])
fill(vec.begin(), vec.end(), -INF);
if(type == 1) up_dfs(1);
else if(type == 2) down_dfs(1);
else if(type == 3) add_human();
else erase_human();
for(int u = 1; u <= n; u ++)
for(int i = 0; i <= siz[ch[u][0]]; i ++)
for(int j = 0; j <= siz[ch[u][1]]; j ++)
if(dp[cur][u][i][j] != -INF)
dp[cur][u][i][j] += r[u] + in[ch[u][0]][i] + in[ch[u][1]][j] + out[u][human_number - i - j];
}
long long res = -INF;
for(int u = 1; u <= n; u ++)
for(auto &vec : dp[cur][u])
for(auto x : vec) res = max(res, x);
if(res == -INF) cout << "No solution." << '\n';
else cout << res << '\n';
return 0;
}
H. 二进制
题目描述
今天也是喜欢二进制串的一天,小 F 开始玩二进制串的游戏。
小 F 给出了一个这里有一个长为 \(n\) 的二进制串 \(s\),下标从 \(1\) 到 \(n\),且 \(\forall i\in[1,n],s_i\in \{0,1\}\),他想要删除若干二进制子串。
具体的,小 F 做出了 \(n\) 次尝试。
在第 \(i\in[1,n]\) 次尝试中,他会先写出正整数 \(i\) 的二进制串表示 \(t\)(无前导零,左侧为高位,例如 \(10\) 可以写为 \(1010\))。
随后找到这个二进制表示 \(t\) 在 \(s\) 中从左到右 第一次 出现的位置,并删除这个串。
注意,删除后左右部分的串会拼接在一起 形成一个新的串,请注意新串下标的改变。
若当前 \(t\) 不在 \(s\) 中存在,则小 F 对串 \(s\) 不作出改变。
你需要回答每一次尝试中,\(t\) 在 \(s\) 中第一次出现的位置的左端点以及 \(t\) 在 \(s\) 中出现了多少次。
定义两次出现不同当且仅当出现的位置的左端点不同。
输入格式
第一行一个正整数 \(n\)(\(1\leq n\leq 1000000\))。
第二行一个长度为 \(n\) 的字符串 \(s\)。保证 \(\forall i\in[1,n], s_i \in \{0, 1\}\)。
输出格式
输出共 \(n\) 行,每行两个整数,第 \(i\) 行表示小 F 进行第 \(i\) 次尝试时开头端点的位置以及相应的字符串出现的次数。
若这次尝试失败,则当前行输出 \(-1\ 0\)。
样例
样例输入 #1
20
01001101101101110010
样例输出 #1
2 11
5 5
4 5
11 1
4 2
7 1
-1 0
-1 0
-1 0
-1 0
-1 0
-1 0
-1 0
-1 0
-1 0
-1 0
-1 0
-1 0
-1 0
-1 0
提示
如果你的复杂度是好的,请相信常数。
请注意输入输出效率。
题解
询问有什么特点?串长是 \(\mathcal{O}(\log n)\) 的,因此我们不妨按照询问串长度从小到大枚举,每次将当前长度的所有子串存下来,询问的时候暴力重建删除串前面的 \(\mathcal{O}(\log n)\) 个子串。
可以用树状数组维护每个下标前面还有多少个没有被删除的下标,总时间复杂度是 \(\mathcal{O}(n \log^2 n)\) 的。
好像有人 \(\mathcal{O}(n)\) 把标算爆了但是我不会www
code for H
// 实现参考loj提交1956881
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int n, A[N], pre[N], nxt[N]; char S[N];
vector<int> vec[N];
int val[N], id[N];
struct Fenwick {
int C[N];
inline void Add(int p, int x) {while(p <= n) C[p] += x, p += p & -p; }
inline int Ask(int p) {int r = 0; while(p) r += C[p], p -= p & -p; return r; }
} BIT;
int main() {
ios::sync_with_stdio(false), cin.tie(0);
cin >> n >> (S + 1);
for(int i = 1; i <= n; i ++)
A[i] = S[i] - '0', BIT.Add(i, 1);
for(int i = 0; i <= n + 1; i ++)
pre[i] = i - 1, nxt[i] = i + 1;
for(int i = 0; (1 << i) <= n; i ++) {
int Val_L = (1 << i), Val_R = min(n, (1 << i + 1) - 1);
for(int p = pre[n + 1]; p; p = pre[p]) {
val[p] = (val[nxt[p]] >> 1) | (A[p] << i);
id[p] = id[nxt[p]] + 1;
if(id[p] > i && val[p] >= Val_L && val[p] <= Val_R) vec[val[p]].emplace_back(p);
}
for(int x = Val_L; x <= Val_R; x ++) {
int a = n + 1, b = 0;
static bool vis[N];
for(auto t : vec[x])
if(!vis[t] && val[t] == x && id[t] > i)
a = min(a, t), b ++, vis[t] = true;
for(auto t : vec[x])
vis[t] = false;
if(b != 0) {
cout << BIT.Ask(a) << ' ' << b << '\n';
BIT.Add(a, -(i + 1));
for(int k = 1, p = a; k <= i + 1; k ++, p = nxt[p])
pre[nxt[p]] = pre[p], nxt[pre[p]] = nxt[p], val[p] = 0;
for(int k = 1, p = pre[a]; p && k <= i; k ++, p = pre[p]) {
val[p] = (val[nxt[p]] >> 1) | (A[p] << i);
id[p] = id[nxt[p]] + 1;
if(id[p] > i && val[p] >= Val_L && val[p] <= Val_R) vec[val[p]].emplace_back(p);
}
} else cout << "-1" << ' ' << "0" << '\n';
}
for(int x = Val_L; x <= Val_R; x ++)
vec[x].clear();
}
return 0;
}
I. 分治乘法
题目描述
小艾想要挑战分治乘法。TA 将策略抽象成了如下问题:
现在给定一个目标集合 \(T\),该集合是 \(\{1,\dots,n\}\) 的一个子集(\(1\leq n\leq 5\times 10^5\))。你需要通过一系列操作构造一些集合最后得到 \(T\),具体来说有以下三种操作:
- 创造一个大小为一的集合 \(|S|=1\)。
- 将已经被构造出的两个不交集合 \(A, B\) 并起来,得到 \(A\cup B\)。
- 将已经被构造出的一个集合 \(A\) 进行平移,也即 \(A+x = \{ a+x : a\in A \}\)。
一个已经被构造出的集合可以在之后被使用多次。同时你需要保证操作过程中出现的所有集合都是 \(\{1,\dots,n\}\) 的子集。
你的代价是构造出的所有集合的大小之和,你不需要最小化代价,只需要让代价控制不超过 \(5\times 10^6\) 即可。你用的操作数量也不应超过 \(10^6\)。
输入格式
第一行输入一个正整数 \(n\)。
接下来一行输入一个 01 串,长度为 \(n\),第 \(x\) 位为 1 表示 \(x\in T\),否则 \(x\notin T\),保证 \(T\) 非空。
输出格式
第一行输出一个正整数 \(m\) 表示你使用的操作数量。
接下来 \(m\) 行,每行描述一个操作,设第 \(i\) 次操作得到的集合为 \(T_i\):
1 x表示创造一个大小为一的集合 \(\{x\}\)。2 x y表示将不交集合 \(T_x, T_y\) 并起来。3 x y表示将已经被构造出的一个集合进行平移,也即 \(T_x+y\)。
你需要保证所有操作满足题目要求,并且最后一次操作产生的集合是 \(T\)。
样例
样例输入 #1
5
11011
样例输出 #1
5
1 1
1 4
2 1 2
3 3 1
2 3 4
- 第一次操作:创造集合 \(T_1=\{1\}\)。
- 第二次操作:创造集合 \(T_2=\{4\}\)。
- 第三次操作:将 \(T_1, T_2\) 并起来,得到 \(T_3=\{1,4\}\)。
- 第四次操作:将 \(T_3\) 平移 \(1\),得到 \(T_4=\{2,5\}\)。
- 第五次操作:将 \(T_3, T_4\) 并起来,得到 \(T_5=\{1,2,4,5\}\)。这就得到了 \(T\)。
这个方案的总代价是 \(1 + 1 + 2 + 2 + 4 = 10\)。
提示
如果你的复杂度是好的,请相信常数。
题解
std是四毛子有点抽象了,这里说一个比较难卡(至少目前没有被卡掉)的混乱中立做法。
首先还是考虑不用3操作而是直接分治,这是 \(\mathcal{O}(n \log n)\) 的,理论上把它除以2就行了。肯定是用3操作。
具体一点的话,每次分治选一个mid,完了之后把两边的公共部分弄出来单独做一次,只在左边、右边的单独做,Huffman树合并即可。
当然,本题肯定有各种各样的做法,这里仅列一个比较简单的。
code for I
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10, M = 5e6 + 10;
int n; char S[N];
vector<array<int, 3>> ans;
inline int calc(int op, int x = 0, int y = 0) {
if(op == 1) ans.push_back({1, x, 0});
else ans.push_back({op, x, y});
return ans.size();
}
int solve(vector<int> vec) {
if(vec.size() == 1)
return calc(1, vec.back());
vector<int> L, R, Com;
int mid = vec[vec.size() >> 1], Le = vec[0], Ri = vec.back();
static bool vis[2 * N];
for(auto x : vec) if(x >= mid) vis[x] = true;
for(auto x : vec)
if(x < mid)
(vis[x + (mid - Le)] ? Com : L).emplace_back(x);
for(auto x : vec) vis[x] = !vis[x];
for(auto x : vec)
if(x >= mid && !vis[x - (mid - Le)]) R.emplace_back(x);
for(auto x : vec) vis[x] = false;
priority_queue<pair<int, int>> Q;
if(!L.empty()) Q.push({-(int)L.size(), solve(L)});
if(!R.empty()) Q.push({-(int)R.size(), solve(R)});
if(!Com.empty()) {
int p = solve(Com);
Q.push({-(int)Com.size(), p});
Q.push({-(int)Com.size(), calc(3, p, mid - Le)});
}
assert(!Q.empty());
while(Q.size() > 1) {
auto u = Q.top(); Q.pop(); auto v = Q.top(); Q.pop();
Q.push({u.first + v.first, calc(2, u.second, v.second)});
}
return Q.top().second;
}
int main() {
ios::sync_with_stdio(false), cin.tie(0);
cin >> n >> (S + 1);
vector<int> vec;
for(int i = 1; i <= n; i ++)
if(S[i] == '1') vec.emplace_back(i);
solve(vec);
cout << ans.size() << '\n';
for(auto vec : ans) {
if(get<0>(vec) == 1) cout << get<0>(vec) << ' ' << get<1>(vec) << '\n';
else cout << get<0>(vec) << ' ' << get<1>(vec) << ' ' << get<2>(vec) << '\n';
}
return 0;
}
J. 套娃
题目描述
我们定义一个集合的 \(\operatorname{mex}\) 是最小的不在 \(S\) 中的非负整数。
给定一个序列 \(a_1,\dots,a_n\),对于每个 \(1\leq k\leq n\),我们按照如下方式定义 \(b_k\):
- 对于 \(a\) 的所有长为 \(k\) 的子区间,求出这个子区间构成的数集的 \(\operatorname{mex}\)。
- 对于求出的所有 \(\operatorname{mex}\),求出这个数集自己的 \(\operatorname{mex}\),记为 \(b_k\)。
请你求出序列 \(b\)。
输入格式
第一行输入一个正整数 \(n\)(\(1\leq n\leq 10^5\))。
第二行输入 \(n\) 个整数 \(a_1,\dots,a_n\)(\(0\leq a_i\leq n\))。
输出格式
一行输出 \(n\) 个整数 \(b_1,\dots,b_n\)。
样例
样例输入 #1
6
0 0 0 1 2 3
样例输出 #1
2 3 4 0 0 0
题解
首先给出一个引理:对于每个值 \(v \in [0, n]\),它们出现的位置将整个序列中不是 \(v\) 的部分分成了若干个小区间(每个区间都是极大的不含 \(v\) 的区间),所有 \(v \in [0,n]\) 的区间个数和是 \(\mathcal{O}(n)\) 的,具体的,一个上界是 \(2n\)。
证明是显然的,值 \(v\) 至多将序列拆成 \(cnt_v+1\) 个不含 \(v\) 的小区间,其中 \(cnt_v\) 指 \(v\) 的出现次数,求和即得。
那么我们可以怎么做呢?从小到大枚举 \(v\),那么 \(\operatorname{mex}=v\) 的子区间一定在划分为的小区间内部(否则含有自然数 \(v\)),而若一个区间内存在一个 \(\operatorname{mex}=v\) 的小区间,那么整个子区间的 \(\operatorname{mex}\) 也是 \(v\)(因为它不含 \(v\))。
所以假如我们可以在每次用 \(v\) 划分序列的时候,对每个小区间找到小区间的长度最小的 \(\operatorname{mex}=v\) 的子区间,设其长度为 \(x\),小区间的总长为 \(y\),我们就可以得到:对于原序列的长度为 \([x,y]\) 的子区间,一定有 \(\operatorname{mex}=v\) 的。
假如可以 \(\mathcal{O}(\log n)\) 单次对每个小区间都这样做,我们就可以得到 \(\operatorname{mex}=v\) 的子区间的长度都可以是多少,然后就可以扫描线做,时间复杂度 \(\mathcal{O}(n \log n)\).
这就是一个可做的问题了,从小到大枚举 \(v\),维护 \(p_i=j\) 表示最小的 \(j\) 使得 \(A_{i..j}\) 中出现过 \([0,v-1]\)。那么 \(p_i\) 应当是单调不降的(反证可得),按官方题解里的说法是构成一个阶梯形。
用线段树维护 \(p_i\),每次对于每个小区间,线段树上二分出一个该小区间内部最靠右的、 \(p\) 不超过小区间右端点的位置 \(pos\),那么小区间 \(pos\) 及其之前的位置都满足 \(p\) 不超过小区间右端点,再用线段树找到这个区间内部 \(p_i-i+1\) 的最小值,同时将这段小区间的 \(p_i\) 在线段树上维护一下(区间推平)即可,总时间复杂度 \(\mathcal{O}(n \log n)\)。
code for J
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, A[N];
vector<pair<int, int>> vec[N];
namespace get_vec {
namespace SegmentTree {
#define lc (u << 1)
#define rc (u << 1 | 1)
#define mid ((l + r) >> 1)
int minP[N << 2], ans[N << 2], tag[N << 2];
inline void maintain(int u, int l, int r) {
minP[u] = min(minP[lc], minP[rc]);
ans[u] = min(ans[lc], ans[rc]);
tag[u] = 0;
}
inline void Tag(int u, int l, int r, int val) {
minP[u] = val, ans[u] = val - r + 1, tag[u] = val;
}
inline void pushdown(int u, int l, int r) {
if(!tag[u]) return;
Tag(lc, l, mid, tag[u]), Tag(rc, mid + 1, r, tag[u]);
tag[u] = 0;
}
void Build(int u, int l, int r) {
minP[u] = 0, ans[u] = 0, tag[u] = 0;
if(l != r) Build(lc, l, mid), Build(rc, mid + 1, r);
}
void Reset(int u, int l, int r, int L, int R, int val) {
if(l >= L && r <= R) return Tag(u, l, r, val);
pushdown(u, l, r);
if(mid >= L) Reset(lc, l, mid, L, R, val);
if(mid < R) Reset(rc, mid + 1, r, L, R, val);
maintain(u, l, r);
}
int get_pos(int u, int l, int r, int L, int R, int lim) {
if(minP[u] > lim) return -1;
if(l >= L && r <= R) {
if(l == r) return l;
if(minP[rc] <= lim) return get_pos(rc, mid + 1, r, L, R, lim);
else return get_pos(lc, l, mid, L, R, lim);
}
pushdown(u, l, r);
if(mid >= R) return get_pos(lc, l, mid, L, R, lim);
if(mid < L) return get_pos(rc, mid + 1, r, L, R, lim);
int ans = get_pos(rc, mid + 1, r, L, R, lim);
return ans == -1 ? get_pos(lc, l, mid, L, R, lim) : ans;
}
int get_ans(int u, int l, int r, int L, int R) {
if(l >= L && r <= R) return ans[u];
pushdown(u, l, r);
if(mid >= R) return get_ans(lc, l, mid, L, R);
if(mid < L) return get_ans(rc, mid + 1, r, L, R);
return min(get_ans(lc, l, mid, L, R), get_ans(rc, mid + 1, r, L, R));
}
#undef lc
#undef rc
#undef mid
}
inline void insert_vec(pair<int, int> pr, int val) {
vec[pr.first].push_back({val, 1}), vec[pr.second + 1].push_back({val, -1});
}
vector<int> pos[N];
inline void main() {
SegmentTree::Build(1, 1, n);
for(int i = 0; i <= n; i ++) pos[i].emplace_back(0);
for(int i = 1; i <= n; i ++) pos[A[i]].emplace_back(i);
for(int i = 0; i <= n; i ++) pos[i].emplace_back(n + 1);
for(int i = 1; i < pos[0].size(); i ++) {
int l = pos[0][i - 1] + 1, r = pos[0][i] - 1;
if(l <= n) SegmentTree::Reset(1, 1, n, l, min(n, r + 1), r + 1);
if(l > r) continue;
insert_vec({1, r - l + 1}, 0);
}
for(int val = 1; val <= n; val ++) {
for(int i = 1; i < pos[val].size(); i ++) {
int l = pos[val][i - 1] + 1, r = pos[val][i] - 1;
if(l > r) continue;
int pos = SegmentTree::get_pos(1, 1, n, l, r, r);
if(pos == -1) continue;
insert_vec({SegmentTree::get_ans(1, 1, n, l, pos), r - l + 1}, val);
SegmentTree::Reset(1, 1, n, l, pos, r + 1);
}
}
}
}
namespace get_ans {
namespace SegmentTree {
#define lc (u << 1)
#define rc (u << 1 | 1)
#define mid ((l + r) >> 1)
int minv[N << 2];
void Build(int u, int l, int r) {
minv[u] = 0;
if(l != r) Build(lc, l, mid), Build(rc, mid + 1, r);
}
void Add(int u, int l, int r, int p, int x) {
if(l == r) return minv[u] += x, void();
if(p <= mid) Add(lc, l, mid, p, x);
else Add(rc, mid + 1, r, p, x);
minv[u] = min(minv[lc], minv[rc]);
}
int Ask(int u, int l, int r) {
if(l == r) return l;
if(minv[lc] == 0) return Ask(lc, l, mid);
else return Ask(rc, mid + 1, r);
}
inline int Ask() {return minv[1] ? n + 1 : Ask(1, 0, n); }
#undef lc
#undef rc
#undef mid
}
inline void main() {
SegmentTree::Build(1, 0, n);
for(int i = 1; i <= n; i ++) {
for(auto pr : vec[i])
SegmentTree::Add(1, 0, n, pr.first, pr.second);
cout << SegmentTree::Ask() << " \n"[i == n];
}
}
}
int main() {
ios::sync_with_stdio(false), cin.tie(0);
cin >> n;
for(int i = 1; i <= n; i ++) cin >> A[i];
get_vec::main(), get_ans::main();
return 0;
}
K. 三步棋
题目描述
K 家里有一条不成文的规矩。如果家里只有 K 和 H 两个人,那么两个人会通过一种叫作“三步棋”的游戏来决定谁做饭。三步棋的规则与五子棋有一些相似之处。众所周知,五子棋是一种先连出五枚己方棋子者获胜的游戏。与五子棋相同的是,三步棋中双方也轮流在网格状的棋盘上摆放棋子,并根据是否连成指定的图案决定胜负。与五子棋不同的是:
-
三步棋不区分双方的棋子,即可以认为双方执同色棋子进行游戏;
-
在判定时,指定的图案不能旋转;
-
如果连成指定的图案时,棋盘上的棋子数量恰好为 \(3\) 的倍数,则连成指定的图案的一方获胜,否则判定该方负(即对方获胜)。
例如,如果指定的图案为
.o
oo
且当前盘面为
o..o.
o.o..
oo...
o.o..
o..o.
时,认为没有连成给定的折线形图案,其中 o 表示棋子,. 表示空格;但若接下来在第二行第二列放一枚棋子,则连成了给定的图案,对应的棋子使用 @ 表示:
o..o.
o@o..
@@...
o.o..
o..o.
此时盘面上恰有 \(11\) 枚棋子,而 \(11\) 不是 \(3\) 的倍数,所以判定放这枚棋子的玩家,也即先手输掉本局。
在 K 家,为了节约时间,通常使用 \(5\times 5\) 的初始为空的棋盘进行三步棋。同时,每次也只会随机选择一个由不超过 \(4\) 枚棋子组成的四连通图案。显然三步棋不存在平局,所以 K 和 H 约定由输的一方负责做饭。K 想知道,如果自己和 H 都足够聪明,那么以选中的图案进行的三步棋游戏是否为先手必胜;因为如果她更容易赢,她就要偷偷地给自己的妹妹放水。
输入格式
输入文件包含多组数据。
输入的第一行包含一个正整数 \(T\),表示数据组数。保证 \(1\le T\le 200\)。
对于每组数据,输入包含 \(5\) 行,每行包括一个长度为 \(5\) 且仅含 . 及 o 的字符串,表示指定的图案。保证每组数据中 o 至少出现一次,且所有 o 组成一个大小不超过 \(4\) 的四连通块。
输出格式
对于每组数据输出一行。如果输入的图案为先手必胜,则输出 Far,否则输出 Away。
样例
样例输入 #1
3
.....
oo...
.....
.....
.....
.o...
.o...
.....
.....
.....
.....
.....
.....
.ooo.
.....
样例输出 #1
Far
Far
Away
该样例包含三组数据。
第一组数据输入的图案为 \(1\) 行 \(2\) 列的 oo。显然,无论先手将棋子放在棋盘上的哪个位置,后手都只有两种策略:
-
和先手的棋子连成
oo,此时棋盘上只有 \(2\) 枚棋子,故后手立即输掉游戏; -
不和先手的棋子连成
oo,但是接下来轮到先手时,先手可以任意连成oo,此时棋盘上恰有 \(3\) 枚棋子,故先手取胜。
无论是哪种策略,后手都无法取胜,故对于 oo 而言先手必胜。
第二组数据输入的图案为 \(2\) 行 \(1\) 列的图案,与 oo 同理,可知为先手必胜。
第三组数据输入的图案为 \(1\) 行 \(3\) 列的 ooo,可以证明为先手必败。
数据范围
保证 \(1\le T\le 200\)。对于每组数据,保证输入的 \(5\times 5\) 的由 . 和 o 组成的字符矩阵中至少含有一个 o,且所有 o 组成一个大小不超过 \(4\) 的四连通块。
题解
既然所有o构成一个大小不超过4的四联通块,那就不妨对每种联通块的形状分类讨论一下。显然旋转后相同的联通块是本质相同的,下面我们只看每种本质不同的。
当然一种简单粗暴的方法是直接写一个暴力去判断,但是其实手推也是比较有意思的,下面就用手推的做法了。
当只有一个o的时候,显然后手必胜,没什么好说的。
当有两个o的时候,只有一种本质不同的就是两个o连起来变成oo,由于第一个 \(3\) 的倍数是先手放,而先手总可以在那一步放出一个oo,因此先手必胜。
当有三个o的时候,有两种本质不同的联通块,但其实它们的胜负是相同的,分析方法也一致:虽然第一个 \(3\) 的倍数是先手放,但只要后手在放第二个子的时候避开先手,那么先手在放第三个子的时候只有第一步、第三步两颗子,是组不成合法的联通块的,而后手在放第 \(6\) 个子的时候,显然 \(2,4,6\) 步都是自己的,可以组成一个合法联通块,后手必胜。
有四个o的时候呢?先手是肯定不能在第 \(3\) 颗子的时候赢了,后手呢?它只能放 \(2,4,6\) 三个子,看起来是不够的,但是它可以贴着先手第一步放的子来做联通块,三个子就是足够的了。所以后手必胜。
但是其实有一个bug,例如合法联通块是Z形或L形、T形的时候,先手可以将第一个子放到角落上一个必然组不成合法联通块的位置让后手贴不到,因此这三种情况是先手必胜,当是一个 \(1 \times 4\) 的长条或 \(2 \times 2\) 的方形的时候,后手必胜。
code for K
#include <bits/stdc++.h>
using namespace std;
string s[5];
inline string check() {
for(int i = 0; i <= 3; i ++)
for(int j = 0; j <= 3; j ++) {
if(s[i][j] == 'o' && s[i + 1][j] == 'o' && s[i][j + 1] == 'o' && s[i + 1][j + 1] == 'o')
return "Away";
}
for(int i = 0; i <= 1; i ++)
for(int j = 0; j <= 4; j ++) {
bool flag = true;
for(int x = 0; x <= 3; x ++)
flag = flag && (s[i + x][j] == 'o');
if(flag) return "Away";
}
for(int j = 0; j <= 1; j ++)
for(int i = 0; i <= 4; i ++) {
bool flag = true;
for(int x = 0; x <= 3; x ++)
flag = flag && (s[i][j + x] == 'o');
if(flag) return "Away";
}
return "Far";
}
inline void solve() {
for(int i = 0; i < 5; i ++) cin >> s[i];
int cnt = 0;
for(int i = 0; i < 5; i ++)
for(int j = 0; j < 5; j ++)
cnt += (s[i][j] == 'o');
if(cnt == 1) {
cout << "Away" << '\n';
} else if(cnt == 2) {
cout << "Far" << '\n';
} else if(cnt == 3) {
cout << "Away" << '\n';
} else {
cout << check() << '\n';
}
}
int main() {
ios::sync_with_stdio(false), cin.tie(0);
int T; cin >> T;
while(T --) solve();
return 0;
}
L. 勇闯末日塔
题目描述
安宁顷刻今将逝,末日黑云伺隙来。宿命无情何所惧?越其止境冀花开。
为了执行毁灭世界的疯狂计划,一位占用了已死之人躯壳的神秘男子在这颗蓝色的星球上创造出了无数末日塔。这些末日塔会散发出浓密的以太射线,对末日塔附近的几乎所有生物进行精神控制,只有受到特殊加护的人才能免受以太射线控制。
一些受到加护的义勇队对这些末日塔进行了调查,其结果显示:这些末日塔组成了复杂的以太传输网络,持续不断地从大地中吸收以太,并将以太传输到位于帝国的中枢塔。
一队持有特殊加护的英雄决定闯入其中一些末日塔,以期彻底调查并尝试破坏这些末日塔。英雄们破坏掉进入的末日塔后,以太传输网络就会受到影响,因此大家希望选择一些末日塔,将其破坏后能使得网络的最大传输容量降到最低。
作为勇闯末日塔小队的先锋,你再次阅读了小队目前所掌握的所有信息。这次大胆的行动计划最终能否拯救这个世界,眼下恐怕谁都无法事先料定。但为了这颗星球的未来,我们只能放手一搏。
星球的表面是一个中心位于 \((0, 0, 0)\),半径为 \(R\) 的完美球面。星球表面上共有 \(N\) 座末日塔,这些令人毛骨悚然的塔构成了以太传输网络的所有节点。
- 末日塔的高度远小于星球半径,因此我们认为第 \(i (1 \le i \le N)\) 座塔是球面上的一个点 \(\left(x_i, y_i, z_i\right)\)。第 \(i\) 座塔的以太传输效率为 \(q_i\)。
- 保证 \(N\) 座末日塔的位置两两不同。在这 \(N\) 座末日塔中,\(s\) 号塔是以太吸收点,\(t\) 号塔是位于帝国的中枢塔;这两座塔的以太浓度显著高于其它的末日塔,因此只能闯入这两座塔之外的末日塔。
\(N\) 座末日塔之间共有 \(M\) 条传输通道。第 \(j (1 \le j \le M)\) 条传输通道连接 \(u_j, v_j\) 两座末日塔,让它们可以互相传输以太。
- 传输通道是双向的,但单位时间内以太的流向必须是单向的。
- 为了节省不必要的成本,传输通道的两端不会连接相同的塔,也不会有两条传输通道连接相同的末日塔对。
- 为了降低传输距离,第 \(i\) 条传输通道沿着 \(u_j\) 和 \(v_j\) 所在的大圆的劣弧铺设,故其长度 \(r_j\) 为两座末日塔在星球表面的球面距离。为了避免传输通道的互相干扰,对于任意一条传输通道所对应的劣弧,其他传输通道所对应的劣弧只会在该劣弧的两端点上与该劣弧相交。保证由同一条传输通道相连的两座末日塔的位置不是对跖点关系。
- 如果不知道大圆、劣弧、球面距离和对跖点是什么,可以参考题面最后的提示部分。
受到传输效率和通道长度的影响,每条传输通道有各自传输以太的容量上限。
- 具体而言,每个单位时间内,第 \(j\) 条传输通道的容量上限为 \(\frac{Kq_{u_j} q_{v_j}}{r_j^2}\),其中 \(K\) 是给定的常数,\(q_{u_j}, q_{v_j}\) 为该传输通道两端的塔的传输效率,\(r_j\) 为这条传输通道的长度。
整张以太传输网络需要将 \(s\) 号塔吸收的以太沿着传输通道传输到 \(t\) 号塔,并使得单位时间内的以太传输量最大。为此,传输网络会自动确定一个以太传输方案,在满足所有传输通道容量上限的前提下,最大化这一传输量。
- 换句话说,如果将末日塔看作图上的点,传输通道看作边,而传输通道的容量上限对应每条边的容量,那么以太的传输方案应该恰好为 \(s\) 到 \(t\) 的最大流。
虽然没有任何人能保证闯入末日塔之后就一定能将其破坏,但作为勇闯末日塔小队的先锋,你还是想在出发之前计算一下,如果成功破坏了所有将要闯入的末日塔,传输网络单位时间的最大传输量将会降至多少。
- 如果成功破坏了选择的末日塔,与其相连的所有传输通道的容量都将降至 \(0\),其余传输通道容量不发生变化;此时传输网络会自动调节至一个在新的网络中传输量最大的新方案。
- 在最理想的情况下,小队将有机会调查并破坏 \(L\) 座末日塔。因此,需要事先选择 \(L\) 座末日塔(均不能是 \(s\) 或 \(t\)),使得当这 \(L\) 座末日塔都被成功破坏时,传输网络的新的传输方案的以太传输量尽可能地小。
输入格式
输入的第一行包括五个正整数 \(N, M, L, s, t\)(\(3\le N\le 1000\),\(2\le M\le \frac{N(N-1)}{2}\),\(1\le L\le \min\{8,N-2\}\),\(1\le s, t\le N\)),分别表示该传输网络包含的末日塔数量,传输通道数量,有机会闯入的末日塔数量,最主要的以太吸收塔的编号和中枢塔的编号。
输入的第二行包括两个实数 \(R, K\)(\(1\le R\le 10^3\),\(1\le K\le 10^3\)),分别表示星球的半径和计算以太容量时用到的常数。
接下来 \(N\) 行,每行三个实数 \(a_i, b_i, q_i\)(\(0\le a_i\le 1\),\(0\le b_i< 2\),\(1\le q_i \le 10^3\)),描述第 \(i\) 座末日塔的信息,其中 \(q_i\) 表示第 \(i\) 座末日塔的传输能力, \(a_i\) 和 \(b_i\) 共同描述末日塔的位置:令 \(\theta_i = \pi a_i\),\(\varphi_i = \pi b_i\)(如果你习惯使用角度制而不是弧度制,可以将 \(\pi\) 改为 \(180^\circ\)),则 \(\left(x_i, y_i, z_i\right) = \left(R \sin\theta_i \cos\varphi_i, R\sin\theta_i \sin\varphi_i, R\cos\theta_i\right)\)。保证末日塔的位置各不相同。
最后 \(M\) 行,每行两个正整数 \(u_i, v_i\)(\(1\le u_i, v_i\le N\)),表示一条传输通道连接的两座末日塔的编号。保证同一条传输通道连接的两座末日塔不相同且不互为对跖点,没有两条传输通道连接的是相同的末日塔对,且传输网络是连通的。
保证输入的所有实数保留到小数点后第 \(4\) 位。
输出格式
输出一个实数,表示如果成功破坏了将要闯入的末日塔,新的传输网络单位时间的最大传输量。当你的输出与标准输出的相对误差或绝对误差不超过 \(10^{-6}\) 时,我们认为你的输出是正确的。
样例
样例输入 #1
6 11 1 1 6
1.0000 1.0000
1.0000 0.0000 10.0000
0.7500 0.2500 6.0000
0.5000 0.0000 1.0000
0.5000 0.5000 1.0000
0.2500 0.2500 6.0000
0.0000 0.0000 10.0000
1 2
1 3
1 4
2 3
2 4
3 4
3 5
3 6
4 5
4 6
5 6
样例输出 #1
8.105694691387022
以太传输网络如下图所示。图中蓝色球面即为星球表面;紫色点为各末日塔,其中 \(P_i\) 对应输入的第 \(i\) 座末日塔;黄色的线表示各传输通道。

原来的传输网络单位时间最大传输量为 \(188/\pi^2\)。破坏第 \(2\) 个末日塔或第 \(5\) 个末日塔都能使新的传输网络单位时间的最大传输量降至 \(80/\pi^2\),而破坏第 \(3\) 个末日塔或第 \(4\) 个末日塔只能使新的传输网络单位时间的最大传输量降至 \(94/\pi^2\),所以应该选择第 \(2\) 个或第 \(5\) 个末日塔尝试破坏。
样例输入 #2
见题目目录下的 2.in
样例输出 #2
见题目目录下的 2.ans
提示
在三维空间中,我们可以用一个有序的实数三元组 \((x, y, z)\) 来描述一个点的位置,其中 \(x, y, z\) 分别称作这个点的横坐标、纵坐标和竖坐标。
三维空间中一个球心在 \(\left(x_0, y_0, z_0\right)\)、半径为 \(R\) 的球面是指空间中所有满足 \(\left(x-x_0\right)^2 + \left(y-y_0\right)^2+\left(z-z_0\right)^2=R^2\) 的点 \((x,y,z)\) 构成的点集。对于该球面上给定的两个不同点 \(\left(x_1, y_1, z_1\right), \left(x_2, y_2, z_2\right)\),
-
如果它们不是一对对跖点(两个点是对跖点当且仅当它们在空间上的欧氏距离为 \(2R\);也称对径点),则它们和球心不在同一直线上,这三个点唯一确定了一个平面。这个平面与球面的交线被称作“大圆”(great circle)。大圆的弧被这两个点分成了两个部分,其中较短部分的长度称为这两点在该球面上的距离。
-
如果两个点是对跖点,则定义它们在球面上的距离为 \(\pi R\)。
尽管本题不提供直接的可视化工具,但是你仍然可以用下发文件中的 convert.py,将满足本题输入格式的文件转换为可以直接输入至 Geogebra 的绘图指令。convert.py 将从标准输入读入数据,并将转换后的绘图指令输出到标准输出。例如,运行 convert.py,并将输入重定向到 1.in,程序输出如下:
$ python convert.py < 1.in
======= Commands begin =======
x^2+y^2+z^2=1^2
towers = {(1; 0.0 pi; -0.5000 pi), (1; 0.25 pi; -0.2500 pi), (1; 0.0 pi; 0.0000 pi), (1; 0.5 pi; 0.0000 pi), (1; 0.25 pi; 0.2500 pi), (1; 0.0 pi; 0.5000 pi)}
ulist = {1, 1, 1, 2, 2, 3, 3, 3, 4, 4, 5}
vlist = {2, 3, 4, 3, 4, 4, 5, 6, 5, 6, 6}
Zip(CircularArc(O, A, B), A, Zip(towers(i), i, ulist), B, Zip(towers(i), i, vlist))
Sequence(Text("Tower " + (i), towers(i), true), i, 1, 6)
======= Commands end =======
将 ======= Commands begin ======= 与 ======= Commands end ======= 之间的每行指令依次粘贴至代数区的输入框中,即可得到与样例 1 附图中类似的三维对象。你可能需要 安装 Python 3.6 或更高版本来运行 convert.py。
这个转换工具,无疑是善良的出题人无私的馈赠。出题人相信,这个美妙的转换工具,可以给拼搏于 AC 这道题的逐梦之路上的你,提供一个有力的援助。
题解
笔者还不会。
M. 你说得对,但是AIGC
题目描述
你说得对,但是众所周知 AIGC 是当下计算机领域最热门的方向之一,算协的几名成员也对此很有兴趣,经过长时间的奋战,终于研发出了一款全新的语言大模型——ChatSAA。
你说得对,但是当模型即将发布之时,开发团队忽然发现模型存在重大问题——由于开发团队的某名成员沉迷于一款中文二字英文七字的游戏(见样例),导致训练模型时使用的语料库被莫名其妙地污染了,这使得模型生成的句子全都带有一个相同的前缀。
你说得对,但是紧急更换语料库重新训练显然已经来不及了,无奈开发团队只能在文档中注明:本模型的最大特性(而非bug)在于生成文本的前19个字符,这既是模型独特的防伪标记,也充分彰显了算协团队的人文情怀和文化素养。
你说得对,但是一个微不足道的问题在于:这会让人们一眼就能分辨出哪些句子是由 AI 生成的,这会对那些打算用 AI 来写作业的同学很不友好。
你说得对,但是现在你手里有一些句子,这些句子有的是由 ChatSAA 生成的,有的是人类写的(假设人类没有刻意模仿 ChatSAA 的生成特性),你需要写一个程序来辨别二者。
你说得对,但是你的程序应当输入一行,一个字符串 \(s\) 表示需要判断的句子,满足 \(|s| \le 200\),且 \(s\) 由包括空格在内的 ASCII 可见字符(即 ASCII 码在 \(32\sim 126\) 的字符)组成。
你说得对,但是你的程序应当输出一行,一个字符串表示判断结果,如果这句话是 AI 生成的,输出 AI,否则输出 Human。
样例
样例输入 #1
You are right, but "Sao Lei (Winmine)" is a game whose Chinese name contains two characters while English name contains seven.
样例输出 #1
AI
你说得对,但是扫雷(Winmine)是一款中文二字英文七字的游戏。
样例输入 #2
Ni shuo de dui, dan shi zhe ju hua bu shi yi "You are right, but " kai tou de.
样例输出 #2
Human
样例输入 #3
You are wrong. Here is why. The English name of game "G****** I*****" contains 14 characters (including a space), not 7.
样例输出 #3
Human
提示
你说得对,但是如果我说这道题的题面是 AI 生成的,阁下又该如何应对?
题解
经典最后一题放签到。判断一下前19个字符即可。
code for M
#include <bits/stdc++.h>
using namespace std;
int main() {
ios::sync_with_stdio(false), cin.tie(0);
string s; getline(cin, s);
if(s.size() < 19) {
cout << "Human" << '\n';
return 0;
}
if(s.substr(0, 19) == "You are right, but ")
cout << "AI" << '\n';
else
cout << "Human" << '\n';
return 0;
}