uniq path 62, 2435

标签：int divisible Down mem 62 grid path uniq

62. Unique Paths Medium

There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.

The test cases are generated so that the answer will be less than or equal to 2 * 109.

 Example 1:

Input: m = 3, n = 7
Output: 28

Example 2:

Input: m = 3, n = 2
Output: 3
Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down

Constraints:

• 1 <= m, n <= 100


方程： paths[i][j] = path[i-1][j] + path[i][j-1] 

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] mem = new int[m][n];
        mem[0][0] = 1;
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++){
                if(i == 0 && j == 0) continue;
                mem[i][j] = ((i - 1 >= 0) ? mem[i-1][j] : 0)
                    + ((j - 1 >= 0) ? mem[i][j-1] : 0);
            }
        }
        return mem[m-1][n-1];
    }
}

2435. Paths in Matrix Whose Sum Is Divisible by K Hard

You are given a 0-indexed m x n integer matrix grid and an integer k. You are currently at position (0, 0) and you want to reach position (m - 1, n - 1) moving only down or right.

Return the number of paths where the sum of the elements on the path is divisible by k. Since the answer may be very large, return it modulo 109 + 7.

 Example 1:

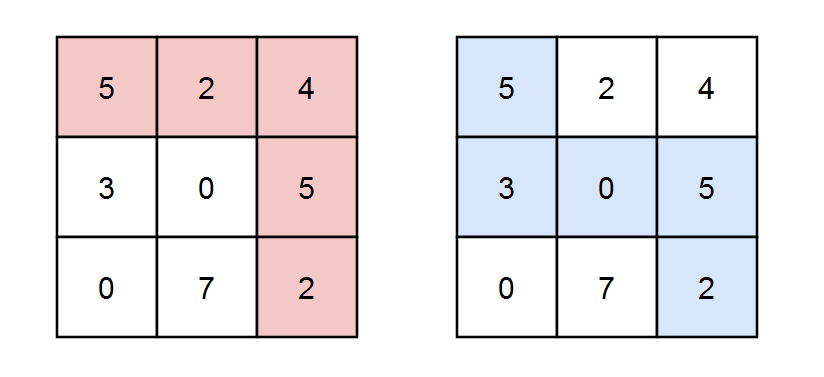
Input: grid = [[5,2,4],[3,0,5],[0,7,2]], k = 3
Output: 2
Explanation: There are two paths where the sum of the elements on the path is divisible by k.
The first path highlighted in red has a sum of 5 + 2 + 4 + 5 + 2 = 18 which is divisible by 3.
The second path highlighted in blue has a sum of 5 + 3 + 0 + 5 + 2 = 15 which is divisible by 3.

Example 2:

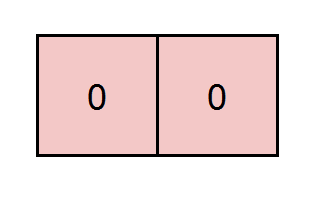
Input: grid = [[0,0]], k = 5
Output: 1
Explanation: The path highlighted in red has a sum of 0 + 0 = 0 which is divisible by 5.

Example 3:

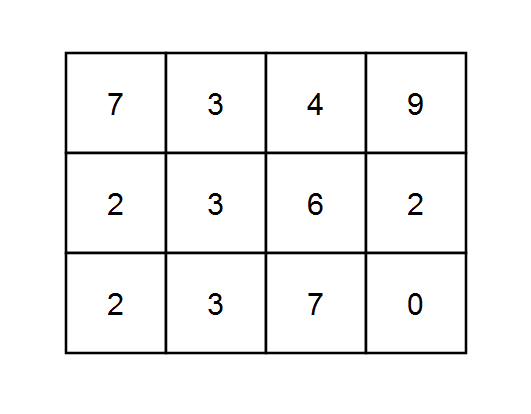
Input: grid = [[7,3,4,9],[2,3,6,2],[2,3,7,0]], k = 1
Output: 10
Explanation: Every integer is divisible by 1 so the sum of the elements on every possible path is divisible by k. 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 5 * 104
• 1 <= m * n <= 5 * 104
• 0 <= grid[i][j] <= 100
• 1 <= k <= 50

class Solution {
    public int numberOfPaths(int[][] grid, int k) {
        int m = grid.length, n = grid[0].length;
        //初始情况下
        int[][][] mem = new int[m][n][k];
        int mod = 1000000007;
        mem[0][0][grid[0][0]%k] = 1;
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(i == 0 && j == 0) continue;
                //遍历左边和上边的所有可能的取模值，加总到当前位置的取模值中
                for(int l = 0; l < k; l++){
                    int val = grid[i][j];
                    if(i > 0)
                        mem[i][j][(val+l)%k] += mem[i-1][j][l]%mod;
                    if(j > 0)
                        mem[i][j][(val+l)%k] += mem[i][j-1][l]%mod;
                }
            }
        }
        //返回k取模值为0的个数
        return mem[m-1][n-1][0] % mod;
    }
}

 

标签：int,divisible,Down,mem,62,grid,path,uniq
From： https://www.cnblogs.com/cynrjy/p/16784127.html