标签：head ListNode struct val next 链表七道指针

合并两个有序链表

我们的 while 循环每次比较 p1 和 p2 的大小，把较小的节点接到结果链表上，看如下 GIF：

形象地理解，这个算法的逻辑类似于拉拉链，l1, l2 类似于拉链两侧的锯齿，指针 p 就好像拉链的拉索，将两个有序链表合并；或者说这个过程像蛋白酶合成蛋白质，l1, l2 就好比两条氨基酸，而指针 p 就好像蛋白酶，将氨基酸组合成蛋白质。

代码中还用到一个链表的算法题中是很常见的「虚拟头结点」技巧，也就是 dummy 节点。你可以试试，如果不使用 dummy 虚拟节点，代码会复杂一些，需要额外处理指针 p 为空的情况。而有了 dummy 节点这个占位符，可以避免处理空指针的情况，降低代码的复杂性。

经常有读者问我，什么时候需要用虚拟头结点？我这里总结下：当你需要创造一条新链表的时候，可以使用虚拟头结点简化边界情况的处理。

比如说，让你把两条有序链表合并成一条新的有序链表，是不是要创造一条新链表？再比你想把一条链表分解成两条链表，是不是也在创造新链表？这些情况都可以使用虚拟头结点简化边界情况的处理。

代码如下：

#include <stdio.h>
#include <stdlib.h>

// 链表节点结构体定义
struct ListNode {
int val;// 节点值
struct ListNode *next;  // 指向下一个节点的指针
};

// 合并两个有序链表的函数
struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2) {
struct ListNode dummy;  // 虚拟头结点
struct ListNode *p = &dummy;// 当前节点指针
struct ListNode *p1 = l1, *p2 = l2;// 两个输入链表的指针

// 遍历两个链表，将值较小的节点逐个接到合并后的链表中
while (p1 != NULL && p2 != NULL) {
if (p1->val > p2->val) {// 如果第一个链表节点的值较大
p->next = p2;   // 将第二个链表节点接到合并链表中
p2 = p2->next;  // 移动第二个链表指针
} else {// 如果第二个链表节点的值较大或相等
p->next = p1;   // 将第一个链表节点接到合并链表中
p1 = p1->next;  // 移动第一个链表指针
}
p = p->next;// 移动合并链表指针
}

// 如果第一个链表还有剩余节点，将剩余节点接到合并链表末尾
if (p1 != NULL) {
p->next = p1;
}

// 如果第二个链表还有剩余节点，将剩余节点接到合并链表末尾
if (p2 != NULL) {
p->next = p2;
}

return dummy.next;  // 返回合并链表的头节点
}

int main() {
// 在这里初始化两个链表 l1 和 l2

// 调用 mergeTwoLists 函数
// struct ListNode* result = mergeTwoLists(l1, l2);

return 0;
}

单链表的分解

在合并两个有序链表时让你合二为一，而这里需要分解让你把原链表一分为二。具体来说，我们可以把原链表分成两个小链表，一个链表中的元素大小都小于 x，另一个链表中的元素都大于等于 x，最后再把这两条链表接到一起，就得到了题目想要的结果。

整体逻辑和合并有序链表非常相似，细节直接看代码吧，注意虚拟头结点的运用：

#include <stdio.h>
#include <stdlib.h>

// 链表结点定义
struct ListNode {
int val;
struct ListNode* next;
};

/**
 * 分割链表，将小于 x 的结点放在一个链表中，大于等于 x 的结点放在另一个链表中
 * @param head 原链表的头结点
 * @param x 分割值
 * @return 分割后的链表的头结点
 */
struct ListNode* partition(struct ListNode* head, int x) {
// 存放小于 x 的链表的虚拟头结点
struct ListNode* dummy1 = (struct ListNode*)malloc(sizeof(struct ListNode));
dummy1->val = -1;
dummy1->next = NULL;

// 存放大于等于 x 的链表的虚拟头结点
struct ListNode* dummy2 = (struct ListNode*)malloc(sizeof(struct ListNode));
dummy2->val = -1;
dummy2->next = NULL;

// p1, p2 指针负责生成结果链表
struct ListNode* p1 = dummy1, * p2 = dummy2;

// p 负责遍历原链表，类似合并两个有序链表的逻辑
// 这里是将一个链表分解成两个链表
struct ListNode* p = head;
while (p != NULL) {
if (p->val >= x) {
p2->next = p;
p2 = p2->next;
}
else {
p1->next = p;
p1 = p1->next;
}
// 不能直接让 p 指针前进，
// p = p->next
// 断开原链表中的每个节点的 next 指针
struct ListNode* temp = p->next;
p->next = NULL;
p = temp;
}

// 连接两个链表
p1->next = dummy2->next;

return dummy1->next;
}
// 创建链表
void createLinkedList(struct ListNode** head, int* arr, int n) {
int i;
struct ListNode* temp, * tail;

// 创建链表头结点
*head = (struct ListNode*)malloc(sizeof(struct ListNode));
(*head)->val = arr[0];
(*head)->next = NULL;
tail = *head;

// 逐个创建链表结点并连接
for (i = 1; i < n; i++) {
temp = (struct ListNode*)malloc(sizeof(struct ListNode));
temp->val = arr[i];
temp->next = NULL;
tail->next = temp;
tail = temp;
}
}
// 打印链表
void printLinkedList(struct ListNode* head) {
struct ListNode* p = head;
while (p != NULL) {
printf("%d ", p->val);
p = p->next;
}
}
int main() {
struct ListNode* head, * result;
int arr[] = { 3, 5, 8, 2, 10, 4 };
int n = sizeof(arr) / sizeof(arr[0]);

// 创建原链表
createLinkedList(&head, arr, n);

printf("Original LinkedList: ");
printLinkedList(head);
printf("\n");

// 分割链表
result = partition(head, 5);

printf("Partitioned LinkedList: ");
printLinkedList(result);
printf("\n");

return 0;
}

如果你不断开原链表中的每个节点的 next 指针，那么就会出错，因为结果链表中会包含一个环：

总的来说，如果我们需要把原链表的节点接到新链表上，而不是 new 新节点来组成新链表的话，那么断开节点和原链表之间的链接可能是必要的。那其实我们可以养成一个好习惯，但凡遇到这种情况，就把原链表的节点断开，这样就不会出错了。

合并K个有序链表

合并 k 个有序链表的逻辑类似合并两个有序链表，难点在于，如何快速得到 k 个节点中的最小节点，接到结果链表上？

这里我们就要用到优先级队列（二叉堆）这种数据结构，把链表节点放入一个最小堆，就可以每次获得 k 个节点中的最小节点：

#include <stdio.h>
#include <stdlib.h>

// 定义链表结构体
struct ListNode {
int val;
struct ListNode* next;
};

// 函数声明
void minHeapify(struct ListNode** pq, int size, int idx);
void swap(struct ListNode** pq, int i, int j);
struct ListNode* mergeKLists(struct ListNode** lists, int listsSize);
void freeList(struct ListNode* node);

// 合并 k 个有序链表的函数
struct ListNode* mergeKLists(struct ListNode** lists, int listsSize)
{
if (listsSize == 0) return NULL;

// 虚拟头结点
struct ListNode* dummy = (struct ListNode*)malloc(sizeof(struct ListNode));
dummy->val = -1;
dummy->next = NULL;

struct ListNode* p = dummy;

// 优先级队列，最小堆
struct ListNode** pq = (struct ListNode**)malloc(listsSize * sizeof(struct ListNode*));
int pqSize = 0;

// 将 k 个链表的头结点加入最小堆
for (int i = 0; i < listsSize; i++) {
if (lists[i] != NULL) {
pq[pqSize++] = lists[i];
}
}

// 最小堆调整
for (int i = (pqSize - 1) / 2; i >= 0; i--) {
minHeapify(pq, pqSize, i);
}

while (pqSize > 0) {
// 获取最小节点，接到结果链表中
struct ListNode* node = pq[0];
p->next = node;

if (node->next != NULL) {
pq[0] = node->next;
minHeapify(pq, pqSize, 0);
}
else {
pqSize--;
pq[0] = pq[pqSize];
minHeapify(pq, pqSize, 0);
}

// p 指针不断前进
p = p->next;
}

// 释放内存
free(pq);

return dummy->next;
}

// 交换链表指针的辅助函数
void swap(struct ListNode** pq, int i, int j)
{
struct ListNode* temp = pq[i];
pq[i] = pq[j];
pq[j] = temp;
}

// 最小堆调整的辅助函数
void minHeapify(struct ListNode** pq, int size, int idx)
{
int smallest = idx;
int left = 2 * idx + 1;
int right = 2 * idx + 2;

if (left < size && pq[left]->val < pq[smallest]->val) {
smallest = left;
}

if (right < size && pq[right]->val < pq[smallest]->val) {
smallest = right;
}

if (smallest != idx) {
swap(pq, idx, smallest);
minHeapify(pq, size, smallest);
}
}

// 释放链表内存的辅助函数
void freeList(struct ListNode* node)
{
struct ListNode* temp;
while (node != NULL) {
temp = node;
node = node->next;
free(temp);
}
}

int main()
{
// 创建链表1: 1->4->5
struct ListNode* head1 = (struct ListNode*)malloc(sizeof(struct ListNode));
head1->val = 1;
head1->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head1->next->val = 4;
head1->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head1->next->next->val = 5;
head1->next->next->next = NULL;

// 创建链表2: 1->3->4
struct ListNode* head2 = (struct ListNode*)malloc(sizeof(struct ListNode));
head2->val = 1;
head2->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head2->next->val = 3;
head2->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head2->next->next->val = 4;
head2->next->next->next = NULL;

// 创建链表3: 2->6
struct ListNode* head3 = (struct ListNode*)malloc(sizeof(struct ListNode));
head3->val = 2;
head3->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head3->next->val = 6;
head3->next->next = NULL;

// 将链表放入数组中
struct ListNode** lists = (struct ListNode**)malloc(3 * sizeof(struct ListNode*));
lists[0] = head1;
lists[1] = head2;
lists[2] = head3;

// 合并链表
struct ListNode* mergedList = mergeKLists(lists, 3);

// 打印合并后的链表
while (mergedList != NULL) {
printf("%d ", mergedList->val);
mergedList = mergedList->next;
}

// 释放链表内存
freeList(mergedList);

// 释放链表数组
free(lists);

return 0;
}

这个算法是面试常考题，它的时间复杂度是多少呢？

优先队列 pq 中的元素个数最多是 k，所以一次 poll 或者 add 方法的时间复杂度是 O(logk)；所有的链表节点都会被加入和弹出 pq，所以算法整体的时间复杂度是 O(Nlogk)，其中 k 是链表的条数，N 是这些链表的节点总数。

单链表的倒数第K个节点

从前往后寻找单链表的第 k 个节点很简单，一个 for 循环遍历过去就找到了，但是如何寻找从后往前数的第 k 个节点呢？

那你可能说，假设链表有 n 个节点，倒数第 k 个节点就是正数第 n - k + 1 个节点，不也是一个 for 循环的事儿吗？

是的，但是算法题一般只给你一个 ListNode 头结点代表一条单链表，你不能直接得出这条链表的长度 n，而需要先遍历一遍链表算出 n 的值，然后再遍历链表计算第 n - k + 1 个节点。

也就是说，这个解法需要遍历两次链表才能得到出倒数第 k 个节点。

那么，我们能不能只遍历一次链表，就算出倒数第 k 个节点？可以做到的，如果是面试问到这道题，面试官肯定也是希望你给出只需遍历一次链表的解法。

这个解法就比较巧妙了，假设 k = 2，思路如下：

首先，我们先让一个指针 p1 指向链表的头节点 head，然后走 k 步：

现在的 p1，只要再走 n - k 步，就能走到链表末尾的空指针了对吧？

趁这个时候，再用一个指针 p2 指向链表头节点 head：

接下来就很显然了，让 p1 和 p2 同时向前走，p1 走到链表末尾的空指针时前进了 n - k 步，p2 也从 head 开始前进了 n - k 步，停留在第 n - k + 1 个节点上，即恰好停链表的倒数第 k 个节点上：

这样，只遍历了一次链表，就获得了倒数第 k 个节点 p2。

上述逻辑的代码如下：

#include <stdio.h>
#include <stdlib.h>

struct ListNode {
int val;
struct ListNode* next;
};

struct ListNode* findFromEnd(struct ListNode* head, int k)
{
struct ListNode* p1 = head;
// p1 先走 k 步
for (int i = 0; i < k; i++) {
p1 = p1->next;
}
struct ListNode* p2 = head;
// p1 和 p2 同时走 n - k 步
while (p1 != NULL) {
p2 = p2->next;
p1 = p1->next;
}
// p2 现在指向第 n - k + 1 个节点，即倒数第 k 个节点
return p2;
}

int main()
{
// 创建链表: 1->2->3->4->5
struct ListNode* head = (struct ListNode*)malloc(sizeof(struct ListNode));
head->val = 1;
head->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->val = 2;
head->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->next->val = 3;
head->next->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->next->next->val = 4;
head->next->next->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->next->next->next->val = 5;
head->next->next->next->next->next = NULL;

// 调用 findFromEnd 函数找到倒数第 2 个节点
struct ListNode* result = findFromEnd(head, 2);

// 打印结果
printf("倒数第 2 个节点的值为：%d\n", result->val);

// 释放链表内存
struct ListNode* curr = head;
while (curr != NULL) {
struct ListNode* temp = curr;
curr = curr->next;
free(temp);
}

return 0;
}

当然，如果用 big O 表示法来计算时间复杂度，无论遍历一次链表和遍历两次链表的时间复杂度都是 O(N)，但上述这个算法更有技巧性。

删除链表的倒数第N个节点

#include <stdio.h>
#include <stdlib.h>

struct ListNode {
int val;
struct ListNode* next;
};

struct ListNode* findFromEnd(struct ListNode* head, int k)
{
struct ListNode* p1 = head;
// p1 先走 k 步
for (int i = 0; i < k; i++) {
p1 = p1->next;
}
struct ListNode* p2 = head;
// p1 和 p2 同时走 n - k 步
while (p1 != NULL) {
p2 = p2->next;
p1 = p1->next;
}
// p2 现在指向第 n - k + 1 个节点，即倒数第 k 个节点
return p2;
}

struct ListNode* removeNthFromEnd(struct ListNode* head, int n)
{
struct ListNode* dummy = (struct ListNode*)malloc(sizeof(struct ListNode));
dummy->val = -1;
dummy->next = head;
struct ListNode* x = findFromEnd(dummy, n + 1);
x->next = x->next->next;
return dummy->next;
}

int main()
{
// 创建链表: 1->2->3->4->5
struct ListNode* head = (struct ListNode*)malloc(sizeof(struct ListNode));
head->val = 1;
head->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->val = 2;
head->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->next->val = 3;
head->next->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->next->next->val = 4;
head->next->next->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->next->next->next->val = 5;
head->next->next->next->next->next = NULL;

// 调用 removeNthFromEnd 函数删除倒数第 2 个节点
struct ListNode* result = removeNthFromEnd(head, 2);

// 打印结果
struct ListNode* curr = result;
while (curr != NULL) {
printf("%d ", curr->val);
curr = curr->next;
}
printf("\n");

// 释放链表内存
curr = result;
while (curr != NULL) {
struct ListNode* temp = curr;
curr = curr->next;
free(temp);
}

return 0;
}

这个逻辑就很简单了，要删除倒数第 n 个节点，就得获得倒数第 n + 1 个节点的引用，可以用我们实现的 findFromEnd 来操作。

不过注意我们又使用了虚拟头结点的技巧，也是为了防止出现空指针的情况，比如说链表总共有 5 个节点，题目就让你删除倒数第 5 个节点，也就是第一个节点，那按照算法逻辑，应该首先找到倒数第 6 个节点。但第一个节点前面已经没有节点了，这就会出错。

但有了我们虚拟节点 dummy 的存在，就避免了这个问题，能够对这种情况进行正确的删除。

单链表的中点

力扣第 876 题「链表的中间结点」就是这个题目，问题的关键也在于我们无法直接得到单链表的长度 n，常规方法也是先遍历链表计算 n，再遍历一次得到第 n / 2 个节点，也就是中间节点。

如果想一次遍历就得到中间节点，也需要耍点小聪明，使用「快慢指针」的技巧：

我们让两个指针 slow 和 fast 分别指向链表头结点 head。

每当慢指针 slow 前进一步，快指针 fast 就前进两步，这样，当 fast 走到链表末尾时，slow 就指向了链表中点。

#include <stdio.h>
#include <stdlib.h>

struct ListNode {
int val;
struct ListNode* next;
};

struct ListNode* middleNode(struct ListNode* head)
{
// 快慢指针初始化指向 head
struct ListNode* slow = head;
struct ListNode* fast = head;
// 快指针走到末尾时停止
while (fast != NULL && fast->next != NULL) {
// 慢指针走一步，快指针走两步
slow = slow->next;
fast = fast->next->next;
}
// 慢指针指向中点
return slow;
}

int main()
{
// 创建链表: 1->2->3->4->5->6
struct ListNode* head = (struct ListNode*)malloc(sizeof(struct ListNode));
head->val = 1;
head->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->val = 2;
head->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->next->val = 3;
head->next->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->next->next->val = 4;
head->next->next->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->next->next->next->val = 5;
head->next->next->next->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->next->next->next->next->val = 6;
head->next->next->next->next->next->next = NULL;

// 调用 middleNode 函数找到链表的中间节点
struct ListNode* result = middleNode(head);

// 打印结果
printf("链表的中间节点的值为：%d\n", result->val);

// 释放链表内存
struct ListNode* curr = head;
while (curr != NULL) {
struct ListNode* temp = curr;
curr = curr->next;
free(temp);
}

return 0;
}

需要注意的是，如果链表长度为偶数，也就是说中点有两个的时候，我们这个解法返回的节点是靠后的那个节点。

另外，这段代码稍加修改就可以直接用到判断链表成环的算法题上。

判断链表是否包含环

判断链表是否包含环属于经典问题了，解决方案也是用快慢指针：

每当慢指针 slow 前进一步，快指针 fast 就前进两步。

如果 fast 最终遇到空指针，说明链表中没有环；如果 fast 最终和 slow 相遇，那肯定是 fast 超过了 slow 一圈，说明链表中含有环。

只需要把寻找链表中点的代码稍加修改就行了：

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

struct ListNode {
int val;
struct ListNode* next;
};

bool hasCycle(struct ListNode* head) {
// 初始化快慢指针，指向头结点
struct ListNode* slow = head;
struct ListNode* fast = head;
// 快指针到尾部时停止
while (fast != NULL && fast->next != NULL) {
// 慢指针走一步，快指针走两步
slow = slow->next;
fast = fast->next->next;
// 快慢指针相遇，说明含有环
if (slow == fast) {
return true;
}
}
// 不包含环
return false;
}

int main() {
// 创建链表: 1->2->3->4->5->6
struct ListNode* head = (struct ListNode*)malloc(sizeof(struct ListNode));
head->val = 1;
head->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->val = 2;
head->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->next->val = 3;
head->next->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->next->next->val = 4;
head->next->next->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->next->next->next->val = 5;
head->next->next->next->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->next->next->next->next->val = 6;
head->next->next->next->next->next->next = head; // 将最后一个节点指向头节点，构成环

// 调用 hasCycle 函数判断链表是否含有环
bool result = hasCycle(head);

// 打印结果
if (result) {
printf("链表含有环\n");
} else {
printf("链表不含有环\n");
}

// 释放链表内存
// 释放链表内存需要特殊处理，否则会造成内存泄漏
struct ListNode* curr = head;
struct ListNode* prev = NULL;
while (curr != NULL) {
if (curr->next == head) {
curr->next = NULL; // 将环断开
}
prev = curr;
curr = curr->next;
free(prev);
}

return 0;
}

环形链表2---找环的起点

#include <stdio.h>
#include <stdlib.h>

struct ListNode {
int val;
struct ListNode* next;
};

struct ListNode* detectCycle(struct ListNode* head) {
struct ListNode* fast = head; // 快指针，每次走两步
struct ListNode* slow = head; // 慢指针，每次走一步

// 使用快慢指针找到链表中的环，如果有环的话
while (fast != NULL && fast->next != NULL) {
fast = fast->next->next; // 快指针每次走两步
slow = slow->next; // 慢指针每次走一步
if (fast == slow) { // 快慢指针相遇，说明有环
break;
}
}

// 上面的代码类似 hasCycle 函数

// 如果没有环，则返回空指针
if (fast == NULL || fast->next == NULL) {
return NULL;
}

// 重新将慢指针指向头节点
slow = head;

// 快慢指针同步前进，相交点就是环的起点
while (slow != fast) {
fast = fast->next;
slow = slow->next;
}

return slow; // 返回环的起点节点
}

int main() {
// 创建链表: 1->2->3->4->5->6，其中6指向3，构成环
struct ListNode* head = (struct ListNode*)malloc(sizeof(struct ListNode));
head->val = 1;
head->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->val = 2;
head->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->next->val = 3;
head->next->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->next->next->val = 4;
head->next->next->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->next->next->next->val = 5;
head->next->next->next->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
head->next->next->next->next->next->val = 6;
head->next->next->next->next->next->next = head->next->next; // 将最后一个节点指向第三个节点，构成环

// 调用 detectCycle 函数找到链表的环起点
struct ListNode* result = detectCycle(head);

// 打印结果
if (result != NULL) {
printf("链表的环起点的值为：%d\n", result->val);
}
else {
printf("链表不含有环\n");
}

// 释放链表内存
// 释放链表内存需要特殊处理，否则会造成内存泄漏
struct ListNode* curr = head;
struct ListNode* prev = NULL;
while (curr != NULL) {
if (curr->next == head) {
curr->next = NULL; // 将环断开
}
prev = curr;
curr = curr->next;
free(prev);
}

return 0;
}

可以看到，当快慢指针相遇时，让其中任一个指针指向头节点，然后让它俩以相同速度前进，再次相遇时所在的节点位置就是环开始的位置。

为什么要这样呢？这里简单说一下其中的原理。

我们假设快慢指针相遇时，慢指针 slow 走了 k 步，那么快指针 fast 一定走了 2k 步：

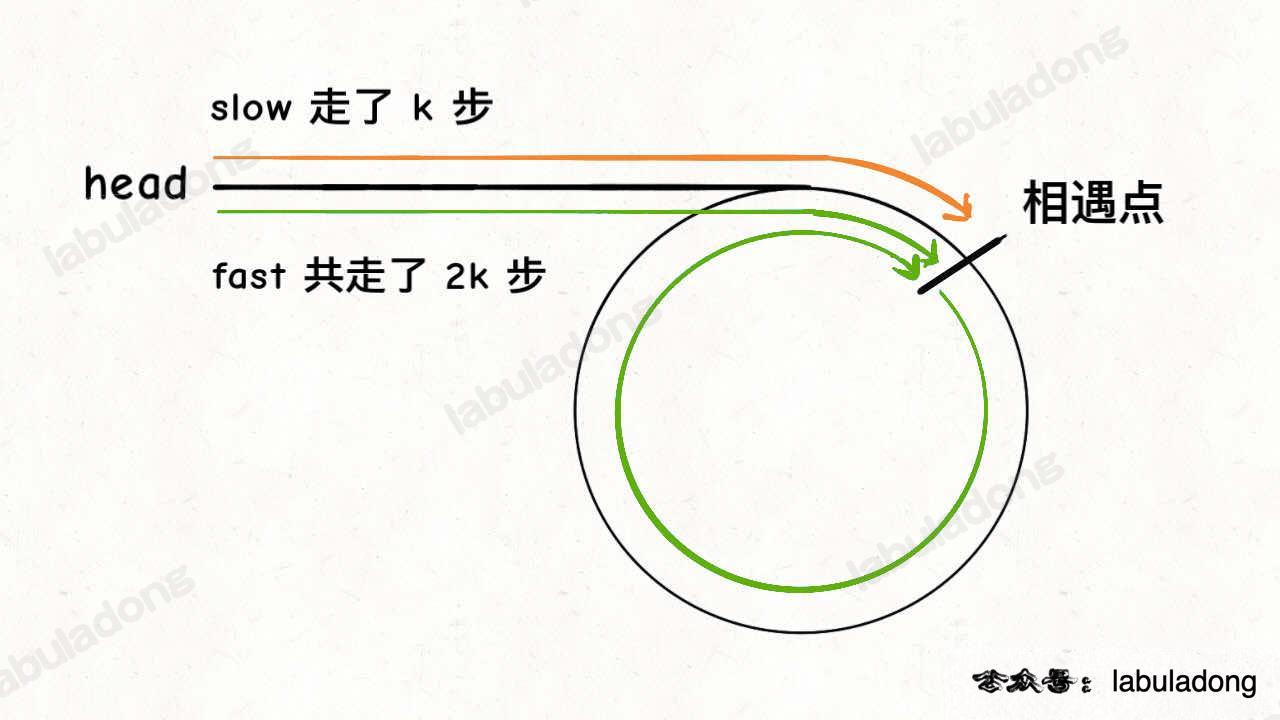
fast 一定比 slow 多走了 k 步，这多走的 k 步其实就是 fast 指针在环里转圈圈，所以 k 的值就是环长度的「整数倍」。

假设相遇点距环的起点的距离为 m，那么结合上图的 slow 指针，环的起点距头结点 head 的距离为 k - m，也就是说如果从 head 前进 k - m 步就能到达环起点。

巧的是，如果从相遇点继续前进 k - m 步，也恰好到达环起点。因为结合上图的 fast 指针，从相遇点开始走k步可以转回到相遇点，那走 k - m 步肯定就走到环起点了：

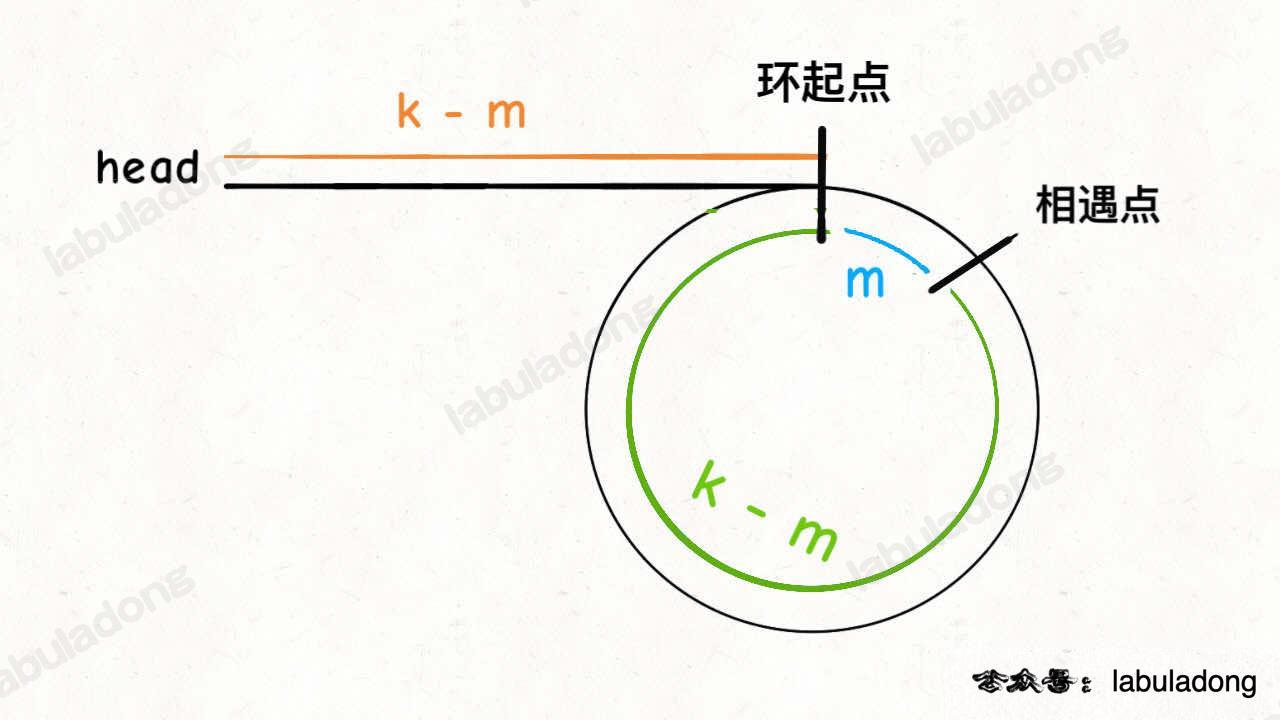
所以，只要我们把快慢指针中的任一个重新指向 head，然后两个指针同速前进，k - m 步后一定会相遇，相遇之处就是环的起点了。

两个链表是否相交

给你输入两个链表的头结点 headA 和 headB，这两个链表可能存在相交。

如果相交，你的算法应该返回相交的那个节点；如果没相交，则返回 null。

比如题目给我们举的例子，如果输入的两个链表如下图：

那么我们的算法应该返回 c1 这个节点。

这个题直接的想法可能是用 HashSet 记录一个链表的所有节点，然后和另一条链表对比，但这就需要额外的空间。

如果不用额外的空间，只使用两个指针，你如何做呢？

难点在于，由于两条链表的长度可能不同，两条链表之间的节点无法对应：

如果用两个指针 p1 和 p2 分别在两条链表上前进，并不能同时走到公共节点，也就无法得到相交节点 c1。

解决这个问题的关键是，通过某些方式，让 p1 和 p2 能够同时到达相交节点 c1。

所以，我们可以让 p1 遍历完链表 A 之后开始遍历链表 B，让 p2 遍历完链表 B 之后开始遍历链表 A，这样相当于「逻辑上」两条链表接在了一起。

如果这样进行拼接，就可以让 p1 和 p2 同时进入公共部分，也就是同时到达相交节点 c1：

那你可能会问，如果说两个链表没有相交点，是否能够正确的返回 null 呢？

这个逻辑可以覆盖这种情况的，相当于 c1 节点是 null 空指针嘛，可以正确返回 null。

按照这个思路，可以写出如下代码：

#include <stdio.h>
#include <stdlib.h>

struct ListNode {
int val;
struct ListNode* next;
};

struct ListNode* getIntersectionNode(struct ListNode* headA, struct ListNode* headB) {
struct ListNode* p1 = headA; // p1 指向 A 链表头结点
struct ListNode* p2 = headB; // p2 指向 B 链表头结点

while (p1 != p2) {
if (p1 == NULL) { // 如果 p1 走到 A 链表末尾，转到 B 链表
p1 = headB;
}
else {
p1 = p1->next; // p1 走到下一个节点
}

if (p2 == NULL) { // 如果 p2 走到 B 链表末尾，转到 A 链表
p2 = headA;
}
else {
p2 = p2->next; // p2 走到下一个节点
}
}

return p1; // 返回交点
}

int main() {
// 创建链表 A: 1->2->3->4->5
struct ListNode* headA = (struct ListNode*)malloc(sizeof(struct ListNode));
headA->val = 1;
headA->next = (struct ListNode*)malloc(sizeof(struct ListNode));
headA->next->val = 2;
headA->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
headA->next->next->val = 3;
headA->next->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
headA->next->next->next->val = 4;
headA->next->next->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
headA->next->next->next->next->val = 5;
headA->next->next->next->next->next = NULL; // 结束链表 A

// 创建链表 B: 6->7->8，其中 8 指向链表 A 的节点 4
struct ListNode* headB = (struct ListNode*)malloc(sizeof(struct ListNode));
headB->val = 6;
headB->next = (struct ListNode*)malloc(sizeof(struct ListNode));
headB->next->val = 7;
headB->next->next = (struct ListNode*)malloc(sizeof(struct ListNode));
headB->next->next->val = 8;
headB->next->next->next = headA->next->next->next; // 8 指向链表 A 的节点 4

// 调用 getIntersectionNode 函数找到链表的交点
struct ListNode* result = getIntersectionNode(headA, headB);

// 打印结果
if (result != NULL) {
printf("链表的交点的值为：%d\n", result->val);
}
else {
printf("链表没有交点\n");
}

// 释放链表内存
// 释放链表内存需要特殊处理，否则会造成内存泄漏
struct ListNode* curr = headA;
struct ListNode* prev = NULL;
while (curr != NULL) {
prev = curr;
curr = curr->next;
free(prev);
}

curr = headB;
prev = NULL;
while (curr != NULL) {
prev = curr;
curr = curr->next;
free(prev);
}

return 0;
}

标签：head,ListNode,struct,val,next,链表,七道,指针
From： https://www.cnblogs.com/lulixiu1999/p/18003474

双指针技巧秒杀七道链表题目