一些废话

更更更好的观感：3ZincBlog。

由于 Github 没法被百度爬到，所以决定 Cnblogs 和 3ZincBlog 同时更新。希望您支持！

DFA：确定有限状态自动机

确定有限状态自动机（DFA，Deterministic Finite Automation），能够按顺序接受一个信号序列并判断其是否符合 DFA 所要判断的条件。

放在 OI 里来说，DFA 一般指：依次输入字符，每输入一次字符就进行一次转移，表示当前字符串从某个状态变到另一个状态，输入完所有字符后，即可直接判断是否符合条件。

将所有状态抽象成点后，把转移当做边，就可以将一个 DFA 看做一张有向图来进行处理。这张有向图中应该有这五部分：

1. \(Q\)，状态集。\(Q\) 中应有该字符串处理时可能存在的所有状态（点）。

2. \(\Sigma\)，字符集。\(\Sigma\) 中有且仅有所有可能的（合法的）输入字符。

3. \(q_0\)，起始状态。表示在还未输入时自动机所处的状态（点）。

4. \(F\)，终点集合。\(F\) 包含所有可接受的（符合条件的）状态（点）。

5. \(\delta\)，转移函数。假设当前处于自动机中的状态（点）\(q \in Q\)，输入了字符 \(c \in \Sigma\)，那么转移后的状态（点）\(q'=\delta(q,c)\)，并且 \(q' \in Q\)。简洁的来说，\(\delta\) 建立了每个状态（点）间关系，或者说边。设计 \(\delta\) 是整个程序中最重要的部分。

接下来，我们再重新描述一下 DFA 怎么工作：

1. 一开始，当前状态（点）\(q=q_0\)。

2. 现在，每输入一个字符 \(c \in \Sigma\)，于是 \(q \to \delta(q,c)\) 并且始终 \(q \in Q\)。

3. 输入完字符串，如果 \(q \in F\)，于是这个字符串是可接受的。不然就不是。

让我们浅尝一下：构造一个 DFA，输入一个二进制串并使它能够判断这个二进制串所对应的数是否偶数。首先，依旧是分五步：\(Q,\Sigma,q_0,F,\delta\)。

考虑，判断二进制串是否为偶数，只需看最后一位是否为 \(0\)。

1. \(Q=\{a_0,a_1\}\)，这是自动机中的两个状态，\(a_0\) 表示当前字符串最后一位为 \(0\)，\(a_1\) 表示最后一位为 \(1\)。

2. \(\Sigma=\{0,1\}\)，二进制串只有这两个字符。

3. \(q_0=a_0\)，当然 \(q_0=a_1\) 也行。为什么？

4. \(F=\{a_0\}\)，表示如果最终停在 \(a_0\)，说明是偶数，可接受。

5. \(\delta\)：\(\delta(q,0)=a_0,\delta(q,1)=a_1\)。

直观一些：

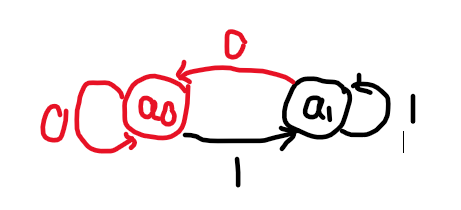
其中红点表示 \(F\) 中的点，黑点表示非 \(F\) 中的点，边上的数表示转移时所输入的字符。

从 DFA 的角度看看 KMP

KMP（Knuth Morris Pratt algorithm，用三个提出者的名字命名），可以检测模式串在匹配串中出现了几次。如果我们从 DFA 的角度考虑：接受一个字符串，当且仅当已知的模式串是该字符串的后缀。

我们发现，在加入字符串的过程中，相当于一个模式串前缀不断尝试与匹配串后缀配对的过程。举个栗子，匹配串 \(T=\texttt{ababc}\) 和模式串 \(S=\texttt{abc}\)：

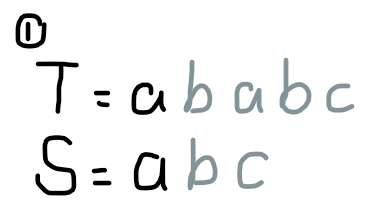
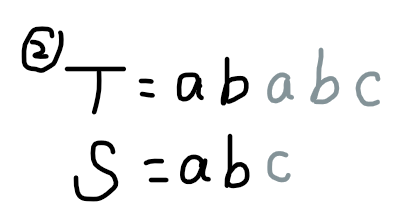
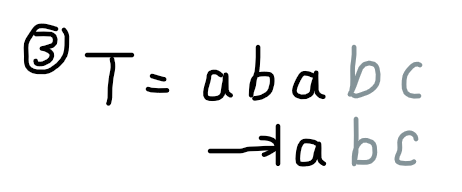
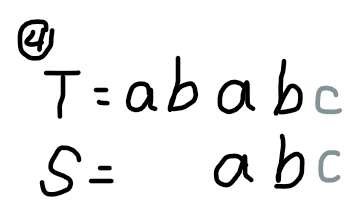
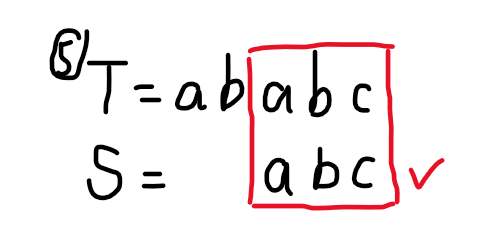
（Fluid 真不戳）

我们发现，这个过程可以生动描述一下：固定 \(T\) 不动，\(S\) 不断与 \(T\) 匹配，若当前字符与 \(S\) 要匹配的字符不匹配，则适当将 \(S\) 向后移动一些距离，使 \(T\) 后缀尽可能多的部分与 \(S\) 前缀中尽可能多的部分相匹配。

写成代码比较简单：（\(ans\) 表示模式串中有多少个匹配串）

scanf("%s%s",T+1,S+1);
int n=strlen(T+1),m=strlen(S+1),ans=0;
for(int i=1,j=0;i<=n;i++) {
    if(j==m||T[i]!=S[j+1]) j= ;
    else j++;
    if(j==m) ans++;
}

那么现在的问题是：如何计算不匹配时，\(j\) 该像哪里跳？

我们继续回到 DFA 的角度来看这个问题：

我们发现，\(j\) 始终在 \(0\) 到 \(m\) 之间，且始终保持 \(T_{i-j+1...i}=S_{1...j}\)。并且 \(T_{1...i-j}\) 对后面的计算没有任何影响，即答案只与 \(T\) 的当前字符与 \(j\) 有关。那么我们考虑设计如下一个 DFA：

1. \(Q=\{0,1,2,3,\cdots,m\}\)，表示所有 \(j\) 的取值。

2. \(\Sigma=\{\texttt{a,b,c,d,...,z}\}\)，表示 \(S\) 和 \(T\) 中所有可能出现的字符。

3. \(q_0=0\)，表示一开始 \(S\) 与 \(T\) 还未开始匹配。

4. \(F=\{m\}\)，表示只接受 \(S\) 是其后缀的字符串。

5. \(\delta(q,c)=q'+1\)，表示寻找最大的 \(q'\) 使得 \(S_{1...q'}=T_{i-q'+1...i}\) 且 \(S_{q'+1}=T_{i+1}\)。

那么现在问题就是，如何快速地求得 \(\delta\)？

由于已知 \(S_{1...q}=T_{i-q+1...i}\)，那么我们相当于要找 \(q'\) 使得 \(S_{1...q'}=S_{q-q'+1...q}\)。相当于 \(S\) 串自己与自己进行匹配！

考虑一个集合 \(c=\{q_1,q_2,q_3,q_4,\cdots,0\}\)，其中任意一个 \(q_i\) 都满足：\(S_{1...q_i}=S_{q-q_i+1...q}\)，那么易知 \(q=\max{c}\)。我们发现：当不匹配时，我们相当于要在 \(c\) 中找一个最大的 \(q'\) 使得 \(S_{q'+1}=T_{i+1}\)。那么我们考虑如何快速求得这个集合 \(c\)？或者说如何快速遍历集合 \(c\)？

答案是：使用链表的方式存储。因为我们只知道当前的 \(q\)，那么求第二大的元素，可以表示为 \(fail[q]\)，第三大的就是 \(fail[fail[q]]\)，以此类推。那么当 \(S_{q+1}\neq T_{i+1}\) 时，我们可以不断地 \(q \to fail[q]\)，来寻找匹配的 \(q_i\)，直到 \(q=0\)。

于是，我们就有：\(\delta(q,c)=\begin{cases}q+1&S_{q+1}=c\\0&q=0\\\delta(fail[q],c)&\mathrm{the\;other}\end{cases}\)

那么如何求 \(fail\) 呢？首先，肯定有 \(fail[1]=0\)。接下来考虑如何预处理其他 \(fail\)。

笔者发现，\(fail[i]\) 可以这样理解：寻找一个最大的 \(j\neq i\) 使得 \(S_{j+1}=S_i\) 并且 \(S_{1...j}=S_{i-j...i-1}\)，这时 \(fail[i]=j+1\)。\(S_{1...j}=S_{i-j...i-1}\) 就是 \(j \in \{fail[i-1],fail[fail[i-1]],...,0\}\)，那么我们可以用 \(\delta\) 来进行求解！

于是，我们就有：\(fail[i]=\begin{cases}0&i=1\\\delta(fail[i-1],S_i)&i\neq1\end{cases}\)

于是，我们通过预处理 \(fail\) 来降低了 \(\delta\) 转移的复杂度。

稍微整理一下，写成程序十分简洁明了：

（将 \(\delta\) 写成 while 循环转移会更加舒服一下，比较常见）

（这里的 \(k\) 充当了 DFA 中当前状态 \(q\)）

int ans=0;
scanf("%s",t+1); n=strlen(t+1);
if(m==1&&t[1]=='#') return 0;
scanf("%s",s+1); m=strlen(s+1);
for(int i=2,k=0;i<=m;i++) {
    while(k&&s[k+1]!=s[i]) k=fail[k];
    if(s[k+1]==s[i]) k++; fail[i]=k;
}
for(int i=1,k=0;i<=n;i++) {
    while(k&&s[k+1]!=t[i]) k=fail[k];
    if(s[k+1]==t[i]) k++;
    if(k==n) ans++,k=fail[k];
    // 这里有一些问题：若 KMP 匹配的串可以重叠，那么这样写是正确的
    // 如果 KMP 匹配的串要完全独立，没有交叉，那么应写成 k=0
}

通过程序，我们来稍微分析一下 KMP 的时间复杂度。

首先，由于每次 \(k\) 最多增加 \(1\)，所以整个循环下来，\(k\) 最多变成 \(n\)；然而 \(fail[k]\) 在最坏情况下也会使 \(k\) 减一，那么整个循环中，\(k\) 至多增减 \(2n\) 次，均摊下来时间复杂度为 \(\mathcal{O(n+m)}\)（包括预处理）。

对于像笔者这样的菜鸟，完全理解 KMP 要不少时间，但只要多花一些心思，仔细思考一下，KMP 还是比较好理解的。

KMP 的进化：AC 自动机

首先，AC 自动机本名叫做 Aho-Corasick Automaton，而不是 Accepted Automation。所以这个算法不能帮助你自动 AC 题目，而是帮助你处理一些字符串问题。

在上面 KMP 一节中，我们是匹配一个模式串；而 AC 自动机更加强大，可以匹配一堆模式串。其实，简单来说，AC 自动机就是 KMP 与 Trie 树的结合体。

（不知道 Trie 的请出门右转百度搜索）

比如我一个字符串 \(\texttt{abbacbc}\) 想要同时匹配 \(\texttt{ac,abba,bc}\) 三个字符串，那么该如何做？比如说，求模式串们各出现了几次？

如果使用传统的 KMP 去做，那么会喜提 \(\mathcal{O(m^2+nm)}\)，比如说共有 \(100\) 个模式串，每个模式串长达 \(100\) 个字符，而匹配串则长达 \(10^6\) 个字符，那阁下该如何应对？妥妥的超时。

而 AC 自动机能够做到的是：\(\mathcal{O(m|S|+n)}\) 的时间复杂度，其中 \(|S|\) 表示模式串长度。

比如上面的例子，我们对 \(\texttt{ac,abba,bc}\) 构造 Trie 树：

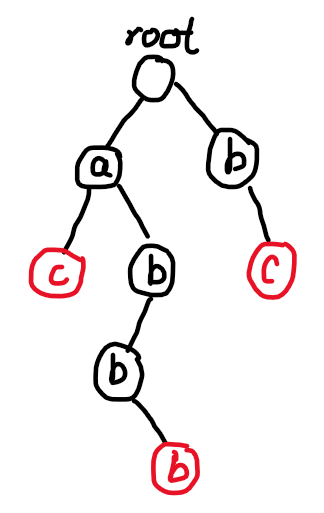
接下来，我们把匹配串放到这棵 Trie 树上跑，跑到红色节点时，相当于进入了一个理想的状态：某个模式串是当前字符串的后缀。此时，这棵 Trie 树就相当于一个 DFA（当然是不完整的）：

1. \(Q=\{root,a_0,a_1,a_2,\cdots\}\)，表示 Trie 树里有哪些节点。

2. \(\Sigma=\{\texttt{a,b,c,...,z}\}\)，字符集不多解释。

3. \(q_0=root\)，一开始为空串，在根节点处。

4. \(F=\{\cdots\}\)，表示所有红色节点（结束节点）。

5. \(\delta(q,c)=q'+1\)，表示从 \(root\) 到 \(q'\) 构成的串是自动机上当前字符串能够找到的最长后缀且 \(q'\) 具有 \(c\) 儿子。

我们仿照上面 KMP 的做法，也设计一个 \(fail\) 来加速 \(\delta\) 转移。

\(\delta(q,c)=\begin{cases}q'&q\;\mathrm{has\;son\;}c\;q'\\root&q=root\\\delta(fail[q],c)&\mathrm{the\;other}\end{cases}\)

（其中 \(q \mathrm{\;has\;son\;}c\;q'\) 表示 \(q\) 有 \(c\) 儿子 \(q'\)）

\(fail[i]=\begin{cases}0&i=root\\\delta(fail[fa[i]],c)&i\neq root\end{cases}\)

（其中 \(fa[i]\) 表示 \(i\) 节点的父亲，\(c\) 表示 \(i\) 节点所对应的字符）

如果觉得不好理解，可以看一看例子中补全的 DFA：

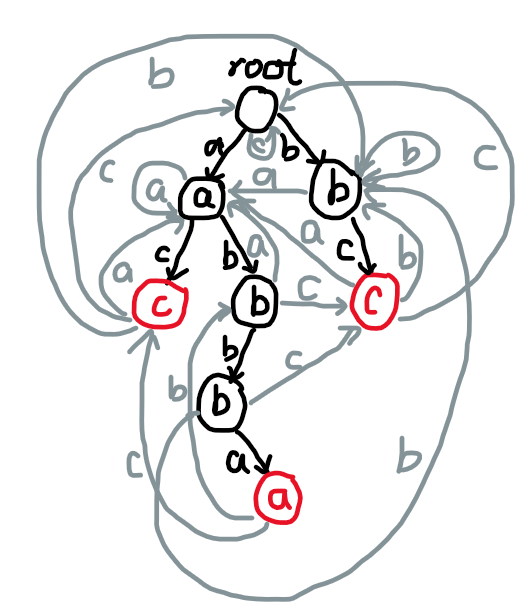
代码有时间再补吧。

END

感谢您的观看！如果觉得不错的话，向别人推荐一下 3ZincBlog 吧！

笔者不才，语言可能不够简洁、准确，希望大神们帮忙指出。

KMP 部分在老师的讲解上稍做了一些修改。