link

Solution

已经被图论虐穿了。。。/kk

首先不难看出对于同一位置，可以用 s1 的字符往 s2 的字符连边，就成了一个大小为 \(20\) 的有向图。然后我们发现其实我们是要构建一个新图，每条边按时间顺序加入，使得原图中的 \(u\to v\) 这条边在新图中可达，且路径时间单调递增，然后让这个新图边数最小。

我们可以对于原图中一个弱连通分量进行单独考虑。注意到假如是 \(n\) 个点，DAG 点数大小最多是 \(m\)，那么新图可以如下构造（借用的湘妹的图）：

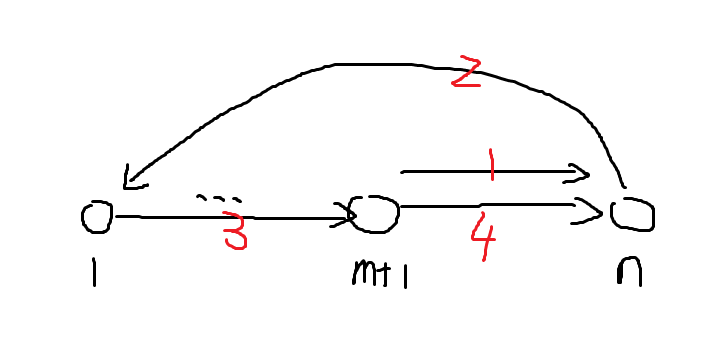
可以发现当且仅当 \(i>j\) 且 \(i,j\) 都在 DAG 中时不可达（需要考虑时间单增的问题），然而这个点对也并不需要考虑。然后你发现这样的话似乎最优性就很显然了。

问题现在就变为了如何找到图中最大的DAG，那么我们可以考虑往点集里面加点即可，每次加的点没有往当前集合的边即可。

Code

#include <bits/stdc++.h>
using namespace std;

#define Int register int
#define MAXN 100005

//char buf[1<<21],*p1=buf,*p2=buf;
//#define getchar() (p1==p2 && (p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
template <typename T> void read (T &x){char c = getchar ();x = 0;int f = 1;while (c < '0' || c > '9') f = (c == '-' ? -1 : 1),c = getchar ();while (c >= '0' && c <= '9') x = x * 10 + c - '0',c = getchar ();x *= f;}
template <typename T,typename ... Args> void read (T &x,Args& ... args){read (x),read (args...);}
template <typename T> void write (T x){if (x < 0) x = -x,putchar ('-');if (x > 9) write (x / 10);putchar (x % 10 + '0');}
template <typename T> void chkmax (T &a,T b){a = max (a,b);}

bool f[1 << 20];
int n,tim,to[25];
char s1[MAXN],s2[MAXN];

int fa[MAXN];
int findSet (int x){return fa[x] == x ? x : fa[x] = findSet (fa[x]);}

void Work (){
	read (n),scanf ("%s%s",s1 + 1,s2 + 1);
	for (Int i = 0;i < 20;++ i) fa[i] = i,to[i] = 0;
	for (Int i = 1;i <= n;++ i){
		int x = s1[i] - 'a',y = s2[i] - 'a';
		to[x] |= 1 << y,fa[findSet (x)] = findSet (y);
	}
	int ans = 40,mxv = 0;
	for (Int i = 0;i < 20;++ i) if (findSet (i) == i) ans --;
	memset (f,0,sizeof (f)),f[0] = 1;
	for (Int S = 0;S < (1 << 20);++ S) if (f[S]){
		chkmax (mxv,__builtin_popcount (S));
		for (Int i = 0;i < 20;++ i) if (!(S >> i & 1) && (to[i] & S) == 0) f[S | (1 << i)] = 1;
	}
	write (ans - mxv),putchar ('\n');
}

signed main(){
	read (tim);
	while (tim --> 0) Work ();
	return 0;
}

extra

可能纯粹是一些闲话吧，想写也只是因为过于滑稽。以前身边没有发生的时候并不认为或者并不感受深刻，现在滑稽感倒是很重了。