- 1.23 P1103 书本整理
题目简化 给定一个数列,和一个数字k,有k次机会将数列中的数字减一。求相邻差值之和最少。
其实如果考虑扔掉k本书,操作起来感觉非常的麻烦。如果考虑留下(n-k)书,再求差值是否会更简便呢?
f[i][j]=min(f[i][j],f[k][j-1]+abs(a[i]-a[k]));
考虑如何排书——
前i本书,选j本书。考虑摆在哪类书的下边。
- 1.178~1.19 P1564 膜拜
思路简述: 考虑前i个人分配机房,需要的最小机房数。再根据题目要求(要么保证整个机房都是同一位神牛的膜拜者,或者两个神牛的膜拜者人数差不超过 m)设计状态转移方程。
f[i]=min(f[i],f[j]+1)(abs(s1-s2)<=m||s1t||s2t)
//t为ij+1段的人数,s1为ij+1段膜拜牛1的人,s2为i~j+1段膜拜牛2的人
- 1.12 P3842 [TJOI2007] 线段
/*死掉的代码与死掉的思路
f[i][j] 表示停在第i行,第j列,且完成改行的线段任务的最短路径
f[i][j1]=min(f[i-1][j2]+cost,f[i][j1])
cost为完成任务的话费,1<=j1<=n&&1<=j2<=n
但仔细思考后就会发现,cost很难求,并且没必要停留在非线段覆盖的点上*/
#include<bits/stdc++.h>
using namespace std;
const int N=2*1e4;
int n,l[N],r[N],f[N][N];
int ans=0x3f3f3f3f;
int work(int i,int j1,int j2){
int cost=1;
int a=l[i],b=r[i];
int s=min(j1,j2),t=max(j1,j2);
if(s<=a) cost+=abs(b-s)+abs(b-t);
else if(s<=b) cost+=abs(s-a)+abs(b-a)+abs(b-t);
else cost+=abs(s-a)+abs(t-a);
return cost;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>l[i]>>r[i];
memset(f,0x3f3f3f3f,sizeof(f));
f[1][1]=0;
for(int j=1;j<=n;j++){
int cost=(j-1);
if(j<=r[1]) cost+=(r[1]-j)*2;
f[1][j]=cost;
}
for(int i=2;i<=n;i++){
for(int j1=1;j1<=n;j1++){
for(int j2=1;j2<=n;j2++){
if(f[i][j1]>f[i-1][j2]){
int tmp=f[i-1][j2]+work(i,j1,j2);
// if(f[i][j1]>tmp){
/// cout<<i<<' '<<j1<<' '<<j2<<' '<<tmp<<' '<<work(i,j1,j2)<<endl;
// }
f[i][j1]=min(f[i][j1],tmp);
}
}
//// cout<<f[i][j1]<<endl;
/// if(i==n) ans=min(f[n][j1],ans);
}
}
/// cout<<ans;
for(int j=1;j<=n;j++){
ans=min(ans,f[n][j]);
}
cout<<ans;
return 0;
}
思考简化掉一下无用的状态空间。
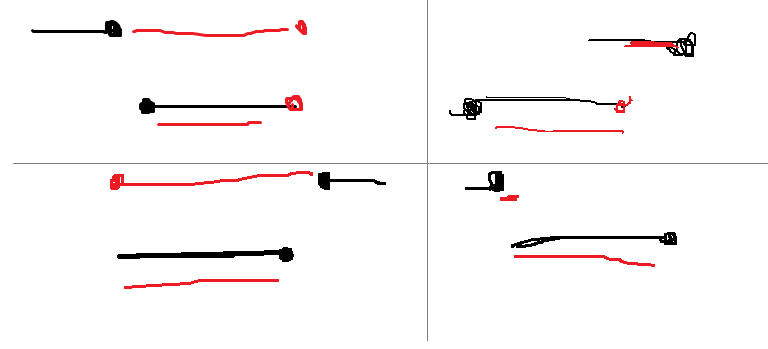
f[i][0/1]表示第i行的完成第i条线段,结束时站在左端点(0)右端点(1)的最优情况
下图是四种转移的情况。
- 1.11 P1095 [NOIP2007 普及组] 守望者的逃离
二维DP
$$f_{i,j}= \max \begin{cases} f_{{i-1},{j-4}} \ f_{{i-1},{j}}+7 \ f_{i,j+10}+60 \end{cases}$$
一维DP
因为题目要求最短的时间,最长的路程。所以如果能使用魔法就尽量使用魔法。但是如果只使用魔法的话,会发现最后的时间里恢复的能量值是不足以使用魔法的,那休息还不如走两步路呢。于是我们就想到用 $f_i$ 来表示第i秒的走的的最长的路程。先处理好,如果只用魔法能走得最长路。在此基础上在处理走路的情况。
//不需要考虑先走路还是先用魔法的问题,因为无论顺序怎么样,到终点花费的时间是一样的。(无后效性)
#include<bits/stdc++.h>
using namespace std;
int m,s,t;
int f[1000006];
int main(){
cin>>m>>s>>t;
for(int i=1;i<=t;i++){
if(m>=10){
m-=10;
f[i]=f[i-1]+60;
}
else{
m+=4; f[i]=f[i-1];
}
}
for(int i=1;i<=t;i++){
f[i]=max(f[i],f[i-1]+17);
if(f[i]>=s){
cout<<"Yes"<<endl<<i;
return 0;
}
}
cout<<"No"<<endl<<f[t];
return 0;
}
贪心
贪心写法,烂尾了。。。
#include<bits/stdc++.h>
using namespace std;
int m,s,t;
int main(){
cin>>m>>s>>t;
int now=0;
for(int i=1;i<=t;i++){
if(m>=10){
if(now+(m/10)*60>=s){
while(now<s){
now+=60;
m/=10;
i++;
if(i==t) break;
}
cout<<"Yes"<<endl;
cout<<i-1;
return 0;
}
now+=min(m/10,t-i+1)*60;
i+=m/10-1;
m-=m/10*10;
}
else{
if( ceil((s-now*1.0)/17)<(10-m)/4||
( (ceil((s-now*1.0)/17)>t-i) &&(10-m)/4+(ceil(s-now*1.0)/60>t-i) ) ){
now+=17;
if(now>=s){
cout<<"Yes"<<endl;
cout<<i;
return 0;
}
}
else m+=4;
}
cout<<i<<" "<<now<<" "<<m<<endl;
}
cout<<"No"<<endl;
cout<<now;
return 0;
}