Alex's whims

题目传送门

题解

构造题，感觉比 G 更难？可能是我不擅长构造。

考虑点的度数，发现一次操作 \(u,v_1,v_2\) 会使 \(deg_{v_1}\) 减 \(1\)，使 \(deg_{v_2}\) 加 \(1\)，即一次操作最多减少一个叶子，那如果存在一个时刻使我们的叶子数量大于 \(3\) 个，下一次若问 \(n-1\) 则直接爆炸，所以要么就是离线下来考虑，要么就是使每时每刻的叶子数量 \(\le 3\)。显然后者更简单。

考虑一个更一般的思路，使 \(1\) 始终为叶子，从点 \(2\) 开始引出两个分叉，大概是这样子的：

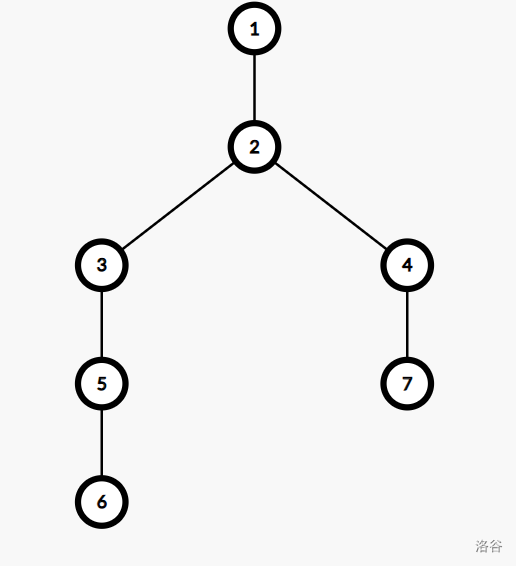
我们强制选择一个分叉，比如左边那个，然后多了就移到右边，少了就从右边补，就可以了。

代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int rd() {
	int s=0,m=0;char ch=getchar();
	while(!isdigit(ch)) {if(ch=='-')m=1;ch=getchar();}
	while( isdigit(ch)) s=(s<<3)+(s<<1)+(ch^48),ch=getchar();
	return m?-s:s;
}
int t,n,q;
vector<int> a,b;
signed main() {
	cin>>t;
	while(t--) {
		n=rd(),q=rd();
		a.clear(),b.clear();
		a.push_back(2);
		for(int i=2;i<=n;i++)
			b.push_back(i),printf("%lld %lld\n",i-1,i);
		while(q--) {
			int d=rd();
			if(a.size()==d||b.size()==d) 
				printf("-1 -1 -1\n");
			else if(a.size()<d) {
				int id=b.size()-(d-a.size());
				printf("%lld %lld %lld\n",b[id],b[id-1],a[a.size()-1]);
				for(int i=id;i<b.size();i++)
					a.push_back(b[i]);
				for(int i=b.size()-1;i>=id;i--)
					b.pop_back();
			}
			else {
				printf("%lld %lld %lld\n",a[d],a[d-1],b[b.size()-1]);
				for(int i=d;i<a.size();i++)
					b.push_back(a[i]);
				for(int i=a.size()-1;i>=d;i--)
					a.pop_back();
			}
		}
	}
	return 0;
}