析合树。对一个排列定义连续段为值域是连续的一段区间。本原连续段(本原段)定义为不与其它任何连续段《相交且不包含》的连续段。即本原段之间只有相离和包含关系。一个连续段可以由若干本原段拼接得到。将所有本原段按照包含关系建树就得到了析合树。
儿子序列是按序列排序,每个点元素是值域区间。儿子排列就是其离散化后的结果。
合点:儿子排列为递增或者递减。特别地,定义叶子为合点。
析点:不是合点的点。
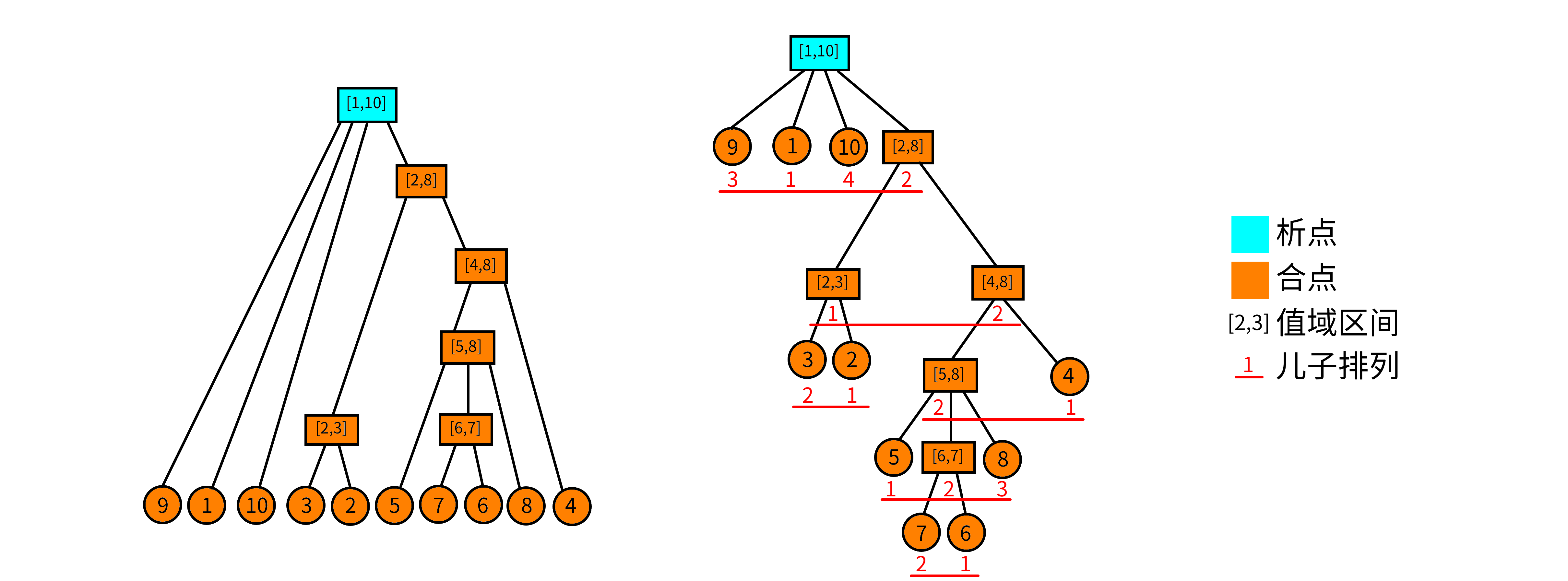
排列 \(9,1,10,3,2,5,7,6,8,4\) 建出的树。图源 oi-wiki。
性质:合点的任意一个儿子排列的区间都是连续段(或者说连续的几棵子树);析点的儿子排列非平凡区间均不是连续段。反证如果存在,最大的非平凡连续段是个本原段,与析合树定义相悖。
从而析点的儿子个数一定 \(\geq 4\)。
就简单看下结构是啥,构造闲的没事的时候再学呃呃。
标签:排列,析点,合点,连续,本原,析合树 From: https://www.cnblogs.com/do-while-true/p/17970015