ARC151D Binary Representations and Queries

题目链接：ARC151D Binary Representations and Queries

非常好思维题。

思路

首先我们会发现每个操作都是 \(\frac{n}{2}\) 的 \(A_i\)，给另外 \(\frac{n}{2}\) 的 \(A_j\) 的增加。

这题直接去维护每个操作时间复杂度会开心的笑。

所以我们换个思路，先去探究一下这题的性质。

考虑一下，是否操作直接可以交换顺序？

反正我觉得不可以

现在我们来证明一下，交换操作不会对答案造成影响（这里交换的前提是要求 \(x_i\neq x_j\)）。

设有操作 \(i,j\)，且 \(x_i\neq x_j,i<j\)。

那么我们可以将 \(2^n\) 个下标分为 \(4\) 个集合。

1.\(b_{x_i}=y_i\) 且 \(b_{x_j}=y_j\)。

2.\(b_{x_i}=y_i\) 且 \(b_{x_j}\neq y_i\)。

3.\(b_{x_i}\neq y_i\) 且 \(b_{x_j}=y_j\)。

4.\(b_{x_i} \neq y_i\) 且 \(b_{x_j}\neq y_j\)。

这里的 \(b_i\) 表示第 \(i\) 位二进制的数。

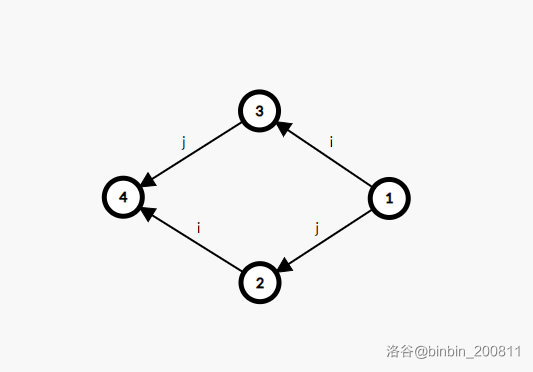
我们将集合 \(u\) 向 \(v\) 连有向边，表示集合 \(u\) 内的下标会给 \(v\) 内的下标做贡献，边的权值为这次操作的编号。

注意这里的权值仅表示操作的编号。

• 如果先做操作 \(i\)，每个集合最终所得到的值如下：

  ​ \(2\gets 1\)。

  ​ \(3 \gets 1\)。

  ​ \(4 \gets 2+3+1\)。

• 如果先做操作 \(j\)，每个集合最终所得到的值如下：

  ​ \(2\gets 1\)。

  ​ \(3 \gets 1\)。

  ​ \(4 \gets 3+2+1\)。

不难发现，每个集合所得到的值并没有发生变化。

也就是说，只要满足 \(x_i\neq x_j\)，我们是可以交换操作的。

有了这个性质，我们考虑把所有 \(x_i\) 相等的操作交换到一起操作。

这样就被分成了两个集合，这两个集合间互相给对方做贡献，方便我们快速统计每个集合收到贡献的系数。

这样就可以快速求 \(A_i\) 了。

时间复杂的 \(O(n\log n)\)。

CODE

#include<bits/stdc++.h>
using namespace std;

#define ll long long
#define mod 998244353

const int maxn=3e5+5;

int n,q;

ll a[maxn],tmp[maxn];

vector<int>tag[20];

int main()
{
    scanf("%d%d",&n,&q);
    for(int i=0;i<(1<<n);i++) scanf("%lld",&a[i]);
    for(int i=1;i<=q;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        tag[x].push_back(y);
    }
    for(int i=0;i<n;i++)
    {
        int x_1=1,y_1=0,x_0=1,y_0=0;//x是自己对自己的贡献系数，y是对方对自己的贡献系数
        for(int k:tag[i])
        {
            if(k) x_0=(x_0+y_1)%mod,y_0=(y_0+x_1)%mod;
            else x_1=(x_1+y_0)%mod,y_1=(y_1+x_0)%mod;
        }
        for(int j=0;j<(1<<n);j++)
        {
            if((j>>i)&1) tmp[j]=(x_1*a[j]%mod+y_1*a[j^(1<<i)]%mod)%mod;
            else tmp[j]=(x_0*a[j]%mod+y_0*a[j^(1<<i)]%mod)%mod;
        }
        for(int j=0;j<(1<<n);j++) a[j]=tmp[j];
    }
    for(int j=0;j<(1<<n);j++) printf("%lld ",a[j]);
}