XOR Tree
\(\mathtt{TAGS}\):树上启发式合并 + 异或 + 贪心
\(\mathtt{ESTIMATION}\):非常好的启发式合并题目
First.如何去除 \(0\) 路径
对于一条路径 \(u \to v\),要使其不为 \(0\) 肯定是将 \(\mathtt{LCA} (u,v)\) 变为 \(2 ^ {30 + x}\) 最好,这样异或值的第 \(30 + x\) 位一定为 \(1\)(因为 \(a_i \le 2 ^ {30}\)),修改之后,\(u,v\) 在 \(\mathtt{LCA} (u,v)\) 为根的子树内的路径都一定不为 \(0\) 了。显然,这样是最优的。
Second.如何快速判断一颗子树下有无 \(0\) 路径
首先,对于 \(u \to v\) 的路径权值 \(dis_{u, v}\) 可以化为 \(dis_{u, 1} \oplus dis_{v, 1} \oplus a_{\mathtt{lca}(u,v)}\)。
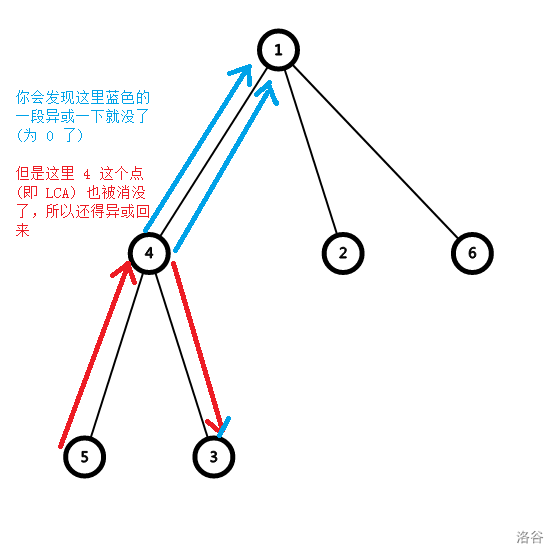
其实知道这个就可以去做 P4551 了。
这个时候可以用一个 set 储存该子树所有 \(dis_{u, 1}\) 的值。然后枚举一个 \(v\) 查找有无 \(dis_{v, 1} \oplus a_u\) 在其中,如果有,那么他们异或起来为 \(0\),就是有 \(0\) 路径。
然后就是把这个子树删除,set 合并到它的父亲上。
这样,大体思路就出来了,暴力的话时间复杂度 \(\text{O}(n ^ 2 \log n)\)(枚举节点的 \(n ^ 2\) 和 set 的 \(\log n\))。
Third.优化时间复杂度
启发式合并,每次将大小小一些的集合合并到大一些的集合上,执行 \(\log n\) 次,节点数就会达到 \(n\)。所以只会合并 \(\log n\) 次。
总时间复杂度为 \(\text{O}(n \log^2 n)\)。
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n;
vector<int> G[N];
int a[N], dis[N];
void dfs(int u, int fa) {
dis[u] = a[u];
if(fa) dis[u] ^= dis[fa];
for (auto v : G[u]) {
if(v != fa) dfs(v, u);
}
}
set<int> s[N]; // 快速查找有无 0 路径
void move (int u, int v) { // 合并
for (auto x : s[u]) s[v].insert(x);
s[u].clear();
}
int ans = 0;
void dfs2(int u, int fa) {
bool mark = 0;
s[u].insert(dis[u]);
for (auto v : G[u]) {
if(v != fa) {
dfs2(v, u);
if(s[u].size() < s[v].size()) swap(s[u], s[v]); // 保证是小的合并至大的里面【启发式合并】
for (auto x : s[v]) mark |= s[u].count(x ^ a[u]); // 如果存在 dis[u] = x ^ a[u] 说明子树中存在异或路径为 0 的路径
move(v, u);
}
}
if(mark) ans ++, s[u].clear(); // 如果存在,那么该节点需要删除
}
signed main() {
ios::sync_with_stdio(0);
cin >> n;
for (int i = 1; i <= n; i ++) cin >> a[i];
for (int i = 1; i < n; i ++) {
int u, v;
cin >> u >> v, G[u].push_back(v), G[v].push_back(u);
}
dfs(1, 0);
dfs2(1, 0);
cout << ans << endl;
return 0;
}