网络流的概念及定义
在一个有向图上选择一个源点,一个汇点,每一条边上都有一个流量上限(以下称为容量),
即经过这条边的流量不能超过这个上界,同时,除源点和汇点外,所有点的入流和出流都相等,
而源点只有流出的流,汇点只有汇入的流。这样的图叫做网络流。
-
源点: 有 \(n\) 个点,有 \(m\) 条有向边,有一个点很特殊,只出不进,叫做 源点。
-
汇点:另一个点也很特殊,只进不出,叫做汇点。
-
容量和流量 :每条有向边上有两个量,容量和流量,从 \(i\) 到 \(j\) 的容量通常用 \(c_{i,j}\) 表示,流量则通常是 \(f_{i,j}\)。通常可以把这些边想象成道路,流量就是这条道路的车流量,容量就是道路可承受的最大的车流量。很显然的,\(f_{i,j} \le c_{i,j}\)。而对于每个不是源点和汇点的点来说,可以类比的想象成没有存储功能的货物的中转站,所有“进入”他们的流量和等于所有从他本身“出去”的流量。
-
最大流:把源点比作工厂的话,问题就是求从工厂最大可以发出多少货物,是不至于超过道路的容量限制。
最大流
下文会提及 Ford-Fulkerson, EK,dinic 两种算法来解决。
Ford-Fulkerson 增广路算法
利用求增广路径来求最大流。实际上相当于非常暴力的求解。时间复杂度为 \(O(m f)\),\(f\) 为最大流数量。根 EK 算法比较类似,使用dfs实现,不多讲,还是看 Ek 更好。
EK 算法
先说时间复杂度:\(O(n m^2)\)
增广路径是啥?就是找到一条从源点开始到汇点的一条路径,用 BFS 遍历。找到这条增广路径上的最小的剩余流量值。也就是边权剩下最短的,然后减去他,若最小值为 \(x\),相当于跑了这个增广路径 \(x\) 遍。
根匈牙利算法和KM算法的增广路径类似,详见 图论基础。
增广路径寻找的过程如下:(from link。)
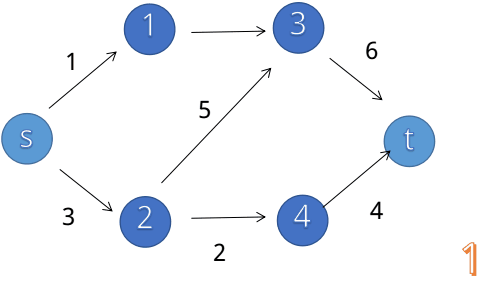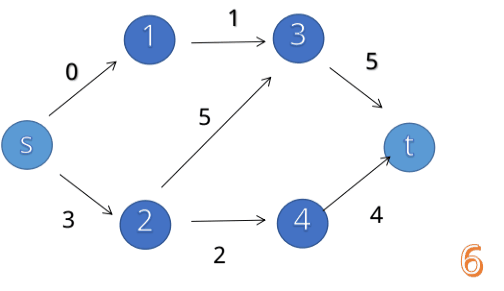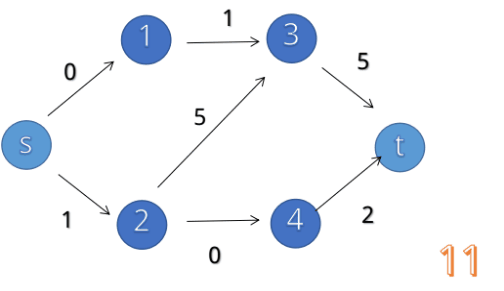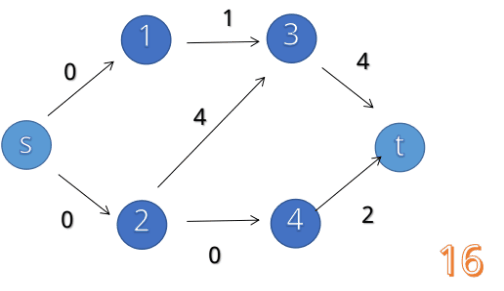
一直找增广路径,知道找不到增广路径就停止。
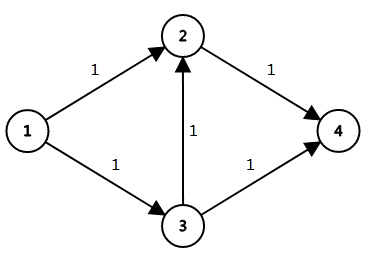
但是会发现,这样的贪心是被 hack 的。因为如果如下图:
按照上述算法模拟可能第一次是 (1->3->2->4),然后最大流为 \(1\)。但是通过用脚模拟,发现了其实实际上是 \(2\)(1->2->4 and 1->3->4)。
上述部分都挺简单,接下来,引入 EK 算法的精髓 建反边。
反向边其实就是一个反悔的机会,也就是让流过的流量流回去。
大佬是这样说的,精炼。
具体来解释 反向边:
因为我们在找到一个 dis (减去的值)后,就会对每条边的容量进行减法操作,而直接更改值就会影响到之后寻找另外的增广路!当我们需要第二次经过该边时,我们就能够通过走反向边恢复这条边的原样。
2023FJZ 说的反向边:
假设你走完了这一条边,然后会影响到后面的边,所以建反向边,后面的边再跑一边,把之前的反向边当做正向边来跑,很显然会知道可以把他消除了。因此,这是一个非常暴力的解决方案。也可以那么理解,这一次先走了这一种方案,统计了最大值,然后清空成初始化,再换一个方案跑,但是反向边巧妙地解决了反悔的问题。正因为如此暴力,所以时间复杂度才回到 \(O(nm^2)\)。
反边只是一个相对的东西,对于这一条正边它的反边就是 (u,v) 倒过来变成 (v,u)。
反边的反边是正边。这样就可以构成了算法的需要。
EK 算法的整体过程如下:来自《NOI辞典》,感觉画的很详细。
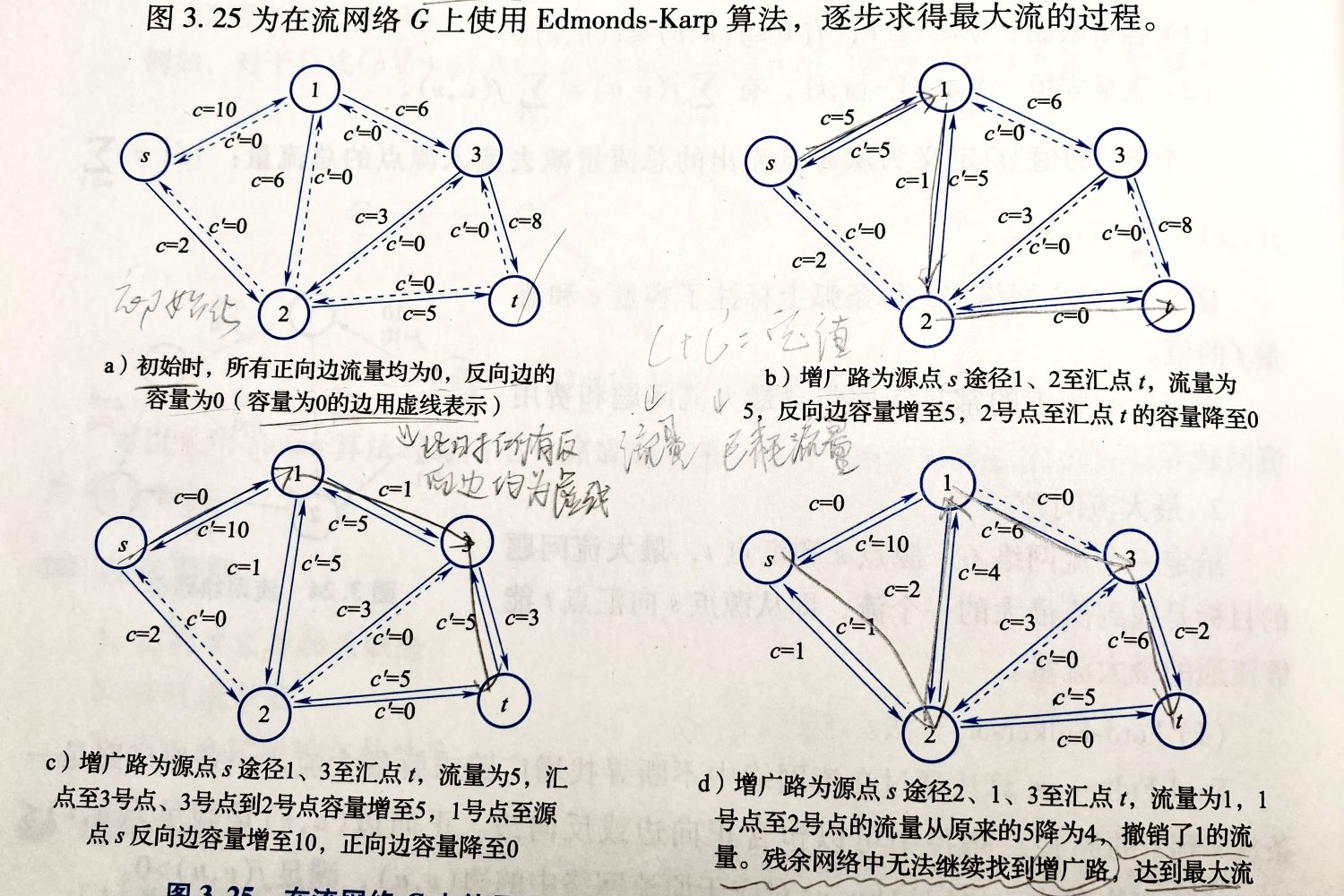
由于数据较小,所以用邻接矩阵来存储,但是链式前向星是更好的选择,下面代码使用的就是链式前向星。
它可以通过边的编号 ^ 1 找到自己的反边,非常巧妙,但是vector存边就无法做到了。因为你要做到记录每一条边的编号。
对于 EK 算法的时间复杂度证明蒟蒻还不是太会,说是 \(O(nm^2)\) 但实际上并没有。通过板子题目 知道 $ n\le 200 , m \le 5000$ 可以通过,是非常的玄学对吧,而且单个测试点耗时最多 110ms,总共耗时 197 ms。哪位大佬留下时间复杂度详细证明给蒟蒻!!
证明如下:
网络流/二分图匹配这种算法都是严重达不到上限的
--- caoshurui 大佬
证毕
为啥呢?玄学。
const int inf = 0x3f3f3f3f,N = 205,M = 5005;
const ll linf = 0x3f3f3f3f3f3f3f3f;
int n,m,s,t;
int mp[N][N];int vis[N],dis[N],pre[N];
int head[N];
struct node{
int to,nxt,val;
}e[2*M];//链式前向星
int tot=1;
void add(int x,int y,int z){
e[++tot].to=y;
e[tot].val=z;
e[tot].nxt=head[x];
head[x]=tot;
e[++tot].to=x;
e[tot].val=0;
e[tot].nxt=head[y];
head[y]=tot;
}
int ans=0;
bool bfs(){//广搜找增广路径
memset(vis,0,sizeof vis);
queue<int> q;
vis[s]=1;
dis[s]=inf;
q.push(s);
while(!q.empty()){
int f=q.front();
q.pop();
for(int i = head[f];i;i=e[i].nxt){//链式前向星遍历
if(e[i].val==0) continue;//值等于零的跳过,只对>0的进行处理。
int to = e[i].to;
if(vis[to]) continue;
vis[to] = 1;
dis[to]=min(dis[f],e[i].val);//这一条增广路径最小的值是多少(最后可以减去他)
pre[to]=i;//记录路径
q.push(to);if(to==t) return true;//找到增广路径返回
}
}return false;
}void update(){//更新,用算出来增广路径的最小值来更新每一条增广路径上的边。
int it=t;
int minn=dis[t];
while(it!=s){
int v=pre[it];
e[v].val-=minn;
e[v^1].val += minn;//反向边做相反的操作
it=e[v^1].to;
}
ans+=dis[t];//更新答案
}
int flag[N][N];
void solve(){
cin >> n >> m ;
s=1,t=m;
for(int i = 1;i <= n;i++){
int u,v,w;cin>>u>>v>>w;
if(!flag[u][v]){//去重操作
add(u,v,w);
flag[u][v]=tot;
}else{
e[flag[u][v]-1].val+=w;
}
}
while(bfs()){//保证有增广路径才可以
update();
}
cout<<ans;
}
dinic 算法后期补上
参考文献
题解 P3376 【【模板】网络最大流】 - Eleven谦 的博客 - 洛谷博客
标签:详讲,源点,增广,int,路径,网络,tot,算法 From: https://www.cnblogs.com/gsczl71/p/17962303