题目描述

给你一个整数x，如果x是一个回文整数，返回true；否则，返回false。
回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。
例如，121是回文，而123不是。

示例 1：

输入：x = 121
输出：true

示例 2：

输入：x = -121
输出：false
解释：从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。

示例 3：

输入：x = 10
输出：false
解释：从右向左读, 为 01 。因此它不是一个回文数。

提示：

• -2³¹ <= x <= 2³¹ - 1

进阶：你能不将整数转为字符串来解决这个问题吗？

题目链接：https://leetcode.cn/problems/palindrome-number/description/

『1』反转一半数字（模拟法）

解题思路：

映入脑海的第一个想法是将数字转换为字符串，并检查字符串是否为回文。但是，这需要额外的非常量空间来创建问题描述中所不允许的字符串。
第二个想法是将数字本身反转，然后将反转后的数字与原始数字进行比较，如果它们是相同的，那么这个数字就是回文。
但是，如果反转后的数字大于int.MAX，我们将遇到整数溢出问题。
按照第二个想法，为了避免数字反转可能导致的溢出问题，为什么不考虑只反转 int 数字的一半？毕竟，如果该数字是回文，其后半部分反转后应该与原始数字的前半部分相同。
例如，输入1221，我们可以将数字 “1221” 的后半部分从 “21” 反转为 “12”，并将其与前半部分 “12” 进行比较，因为二者相同，我们得知数字1221是回文。
题解来源：回文数 - 力扣官方题解

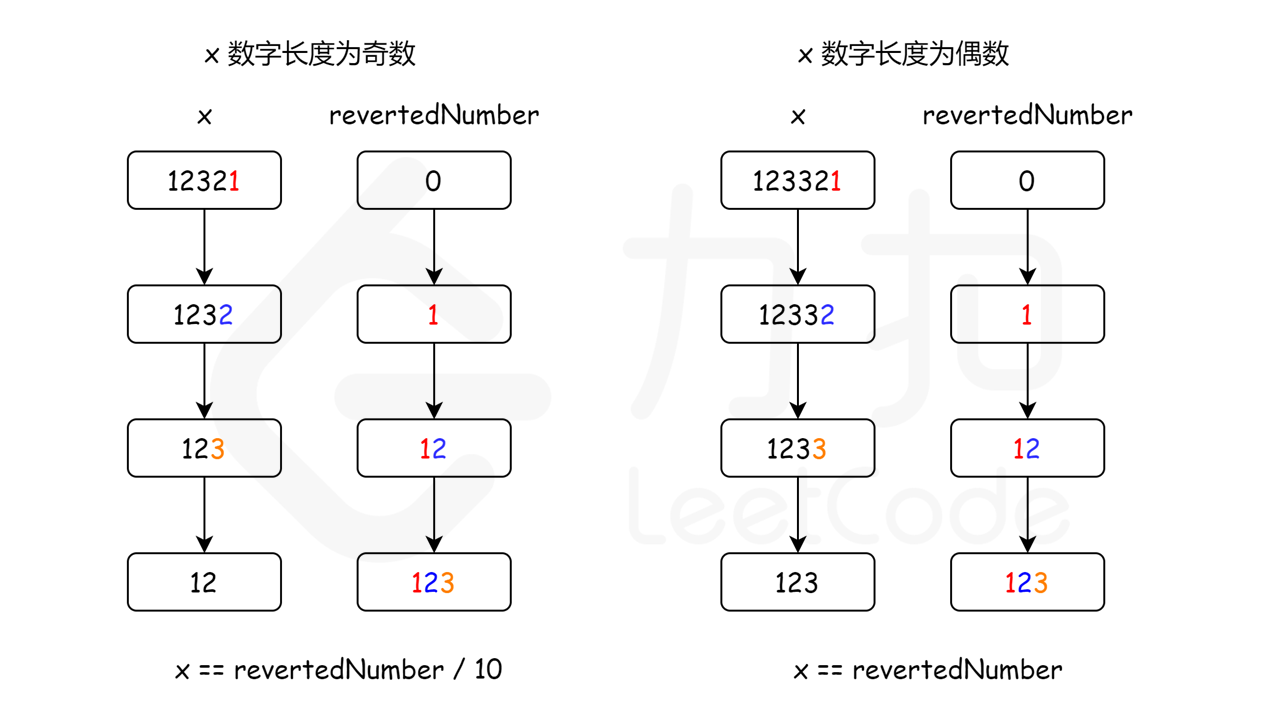
实现代码：

class Solution {
    // Simulation
    // N is the number of digits in the number x  
    // Time Complexity: O(log(N))
    // Space Complexity: O(1)
    public boolean isPalindrome(int x) {
        // 0 是回文数
        if (x == 0) return true;
        // 负数有负号，一定不是回文数
        // 正数若为 10 的整数倍，则其反转后会少一位数，一定不是回文数
        // 目前 x 非零，if 语句中 x < 0 为 false 即 x 为正数才继续判断 x % 10，因此省略 x > 0
        if (x < 0 || x % 10 == 0) return false;
        
        // 用于存储反转后的数
        int rev = 0;
        // 当原始数字小于或等于反转后的数字时，就意味着已反转后半部分数字
        // 若 x 位数为偶数，则反转后 rev 与 x 位数相同
        // 若 x 位数为奇数，则反转后 rev 比 x 多一位数，即 x 中间位置的数
        while (x > rev) {
            // 弹出和推入
            rev = rev * 10 + x % 10;
            x /= 10;
        }
        // 处理偶数位数和奇数位数的情况
        // 若为奇数位数，则 rev / 10 以去除推入 rev 的 x 中间位置的数  
        return x == rev || x == rev / 10;
    }
}