$$\Huge\textbf{\color{black}{二分图}}$$
1. 二分图
二分图,又称二部图,英文名叫 \(Bipartite\ graph\),是节点由两个集合组成,且两个集合内部没有边的无向图
二分图不存在长度为奇数的环,因此可以搜索这张图,如果发现了奇环,那么就不是二分图
P1525 关押罪犯:二分答案后判断二分图 \(\color{white}{二分+二分=四分}\)
2. 二分图最大匹配
从二分图中选出一些边,使得这些边没有公共顶点,且边的数量最大
增广路:一条连通两个未匹配顶点的路径,并且已匹配和未匹配的边在增广路上交替出现
将增广路上的所有边取反可以将匹配数量增加 \(1\)
因为将增广路取反后已匹配点不会变为未匹配点,所以不断寻找增广路就可以找出二分图中的最大匹配
如何找到增广路?
匈牙利算法依次尝试给每一个左部节点 \(x\) 寻找一个匹配的右部节点 \(y\)。右部点 \(y\) 能与左部点 \(x\) 匹配,需要满足以下两个条件之一:
-
\(y\) 本身就是非匹配点。此时无向边 \(x \rightarrow y\) 本身就是非匹配边,自己构成一 条长度为 \(1\) 的增广路
-
\(y\) 已经与左部点 \(x'\) 匹配,但从 \(x'\) 出发能找到另一个右部点 \(y'\) 与之匹配。此时路径 \(x \rightarrow y \rightarrow x' \rightarrow y'\) 为一条增广路
匈牙利算法
struct Hungarian
{
int road[maxn], link[maxn], dfn;
bool dfs(int u)
{
for (int j = g.Last[u], v; j != 0; j = g.Next[j])
{
if (road[v = g.to[j]] == dfn) continue;
road[v] = dfn;
if (link[v] == -1 || dfs(link[v]))
{
link[v] = u;
return 1;
}
}
return 0;
}
int getMaxMatch(int n)
{
int ans = 0;
dfn = 0;
for (int i = 1; i <= n; i++) link[i] = road[i] = -1;
for (int i = 1; i <= n; i++)
{
dfn++;
ans += dfs(i);
}
return ans;
}
}
H;
有一个 \(n\) 行 \(m\) 列的棋盘,其中有的格子不能放置車,求棋盘上最多能放多少个不能互相攻击的車
把每一行,每一列分别看作一个点,对于每一个第 \(i\) 行第 \(j\) 列可以放置車的位置,在第 \(i\) 行的节点和第 \(j\) 行的节点之间连边
如果我们选择一个点放置車,也就是选择图上的一条边,那么这一行和这一列所在的节点都无法再连边,符合二分图最大匹配的定义
因此建完图后求最大匹配即可
解法同上,把每一行被墙分隔开的部分和每一列被墙分隔开的部分分别建立节点,然后求最大匹配
3. 二分图最小覆盖
从二分图中选出一些点,使得任意一条边都有一个端点被选中,且点的数量最小
König 定理:二分图中,最小覆盖个数 \(=\) 最大匹配个数
证明:参考 matrix67大佬的博客 和 OI Wiki
P6062 [USACO05JAN] Muddy Fields G
把每一行中被草地分隔的连续泥地和每一列中被草地分隔的连续泥地分别建点
每块泥地要么被所在行的连续泥地上的木板覆盖,要么被所在列的连续泥地上的木板覆盖,向两者分别连边,最后求图中的最小覆盖个数
4. 二分图最大独立集
从二分图中选出一些点,使得任意两点都不相连,且点的数量最大
二分图中,最大独立集个数 \(=\) 总点数 \(-\) 最小覆盖个数
证明:找最多的不相连的点,等价于在图中去掉最少的点使剩下的点之间没有边,等价于用最少的点覆盖所有的边
对棋盘交替黑白染色,因为骑士能攻击到的格子都与本格不同色,所以两种颜色的格子可以分别作为二分图的两边,再分别对每一个格子能攻击到的格子进行连边,求最大独立集
5. 有向无环图最小路径覆盖
从有向无环图中选出最少的路径,使得图中所有点都被覆盖,且路径间无交点
将原图中的每个点 \(x\) 拆成 \(x\) 和 \(x'\) 两个点
对于每条有向边 \(u \rightarrow v\),在 \(u\) 和 \(v'\) 之间进行连边,最后得到一个二分图
有向无环图的最小路径覆盖数 \(=\) 总点数 \(-\) 拆点后二分图的最大匹配数
总之,二分图问题的关键在于找出问题中分成两部分的点和连接点的边,再明确问题对应的图论模型
$$\Huge\textbf{\color{black}{图的连通性}}$$
1. 有向图的强连通分量与缩点
注:因为作者并没有完全学会 Tarjan 这部分存在部分错误,请不要带脑子观看以下内容,以免产生误导。建议直接看洛谷日报
在有向图中,若任意两个节点都可以互相到达,则称该有向图是强连通图
有向图的极大强连通子图被称为强连通分量(\(Strongly\ Connected\ Components\))
既然强连通分量之间可以相互到达,那么就可以将整个强连通分量缩成一个点
缩点后的图一定是有向无环图,可以进行拓扑排序和动态规划等操作
\(Tarjan\) 求强连通分量
\(Tarjan\) 算法对图进行深度优先搜索,每个点只访问一次,所有发生递归的边就构成了一棵搜索树,这些边被称为图中的树枝边
如果一个节点的子树中所有未被统计为强连通分量的节点都无法回溯到这个节点的上方,那么这些节点构成强连通分量
搜索过程中用 \(dfn_i\) 表示编号为 \(i\) 的节点在 \(DFS\) 过程中第一次被访问时的时间顺序,即时间戳
\(low_i\) 表示 \(i\) 节点的子树中的节点和从 \(i\) 节点的子树中可以通过一条有向边到达的节点的 \(dfn\) 的最小值
因此,在代码实现上,\(low_i\) 会不断被更新为以下几个值的最小值
-
\(i\) 节点的 \(dfn\)
-
可以直接从 \(i\) 节点到达的 \(i\) 的祖先节点的 \(dfn\)
-
可以直接从 \(i\) 节点到达的、可以到达 \(i\) 的祖先的、不是 \(i\) 的子孙节点的节点的 \(dfn\)
-
\(i\) 节点的子节点的 \(low\)
第 \(2\) 和第 \(3\) 种情况描述的节点其实相当于这个节点未被统计为强连通分量
那么如何判断一个节点是不是 \(i\) 在不在强连通分量中呢?
在搜索过程中将一路上经过的节点放进一个栈中,并记录每一个节点是否在栈中
\(i\) 节点完成递归,计算完 \(dfn_i\) 和 \(low_i\) 之后,如果 \(dfn_i = low_i\),那么 \(i\) 节点一定是它所在的强连通分量在搜索树中的根,并且不断出栈直到 \(i\) 本身出栈为止,这些出栈的节点都和 \(i\) 节点在同一个强连通分量中。这样,我们就可以把 \(2\) 和 \(3\) 两种情况统一处理
为什么这样是正确的呢?
首先,这些节点都无法到达 \(dfn\) 比 \(i\) 更小的位置,所以它们肯定在同一个强连通分量中
其次,一个节点完成递归后,被出栈的节点的出边肯定是被统计完了的,所以它们也无法和其它点构成一个更大的强连通分量。如果没有出栈,就相当于它还有出边,且可以连接到更靠前的祖先节点
struct Tarjan
{
int dfnCnt, dfn[maxn], low[maxn];
int sccCnt, scc[maxn], size[maxn];
int stack[maxn], top, inStack[maxn];
void dfs(int u, int fa)
{
dfn[u] = low[u] = ++dfnCnt;
stack[++top] = u, inStack[u] = 1;
for (int i = g.last[u]; i != 0; i = g.next[i])
{
int v = g.to[i];
if (!dfn[v]) dfs(v, u), low[u] = min(low[u], low[v]);
else if (inStack[v]) low[u] = min(low[u], dfn[v]);
}
if (dfn[u] == low[u])
{
sccCnt++;
int t;
do
{
t = stack[top--];
inStack[t] = 0;
scc[t] = sccCnt;
size[sccCnt]++;
}
while (u != t);
}
return;
}
void tarjan(int n)
{
dfnCnt = sccCnt = top = 0;
for (int i = 1; i <= n; i++)
{
if (!dfn[i]) dfnCnt = 0, dfs(i, 0);
}
}
} T;
缩点
for (int i = 1; i <= g.cnt; i++)
{
int u = g.st[i], v = g.to[i];
if (t.scc[u] != t.scc[v])
{
g2.add(t.scc[u], t.scc[v]);
}
}
另外,很多时候需要统计缩点后每个点的出度或入度,以满足题目中的某些条件
2. 无向图的桥和割点
还是 \(Tarjan\)
桥:一条无向边 \((u,v)\) 是桥,当且仅当存在 \(u\) 的子节点 \(v\) 使得 \(dfn_u < low_v\)(前提是其没有重边)
割点:节点 \(u\) 是割点,当且仅当满足 \(1\) 或 \(2\)
-
\(u\) 为搜索树树根,且 \(u\) 有至少两个子树
-
u不为树根,且满足存在 \(u\) 的子节点 \(v\) 使得 \(dfn_u \le low_v\)
struct Tarjan
{
int dfnCnt, dfn[maxn], low[maxn];
int sccCnt, scc[maxn], size[maxn];
int stack[maxn], top, inStack[maxn];
int cut[maxn], cutCnt, bridge[maxm], bridgeCnt;
void dfs(int u, int fa)
{
dfn[u] = low[u] = ++dfnCnt;
stack[++top] = u, inStack[u] = 1;
int child = 0;
for (int i = g.last[u]; i != 0; i = g.next[i])
{
int v = g.to[i];
if (!dfn[v])
{
child++;
dfs(v, u);
low[u] = min(low[u], low[v]);
if (dfn[u] < low[v]) bridge[i] = 1, bridgeCnt++;
if (dfn[u] <= low[v] && fa != 0 && !cut[u]) cut[u] = 1, cutCnt++;
}
else if (inStack[v]) low[u] = min(low[u], dfn[v]);
}
if (fa == 0 && child >= 2 && !cut[u]) cut[u] = 1, cutCnt++;
if (dfn[u] == low[u])
{
sccCnt++;
int t;
do
{
t = stack[top--];
inStack[t] = 0;
scc[t] = sccCnt;
size[sccCnt]++;
}
while (u != t);
}
return;
}
void tarjan(int n)
{
dfnCnt = sccCnt = top = 0;
for (int i = 1; i <= n; i++)
{
if (!dfn[i]) dfnCnt = 0, dfs(i, 0);
}
}
} T;
$$\Huge\textbf{\color{black}{分块}}$$
1. 数列分块
我们可以将一个数列分为多个区间,且每个区间长度大致相同且一般等于 \(\sqrt{n}\)(最后一个除外)
区间修改时,我们可以用一个类似线段树的 \(Lazy\) 标记,使得整个区间可以在 \(O(1)\) 的时间被修改。因为区间个数的规模是 \(\sqrt{n}\),所以总时间复杂度为 \(O(\sqrt{n})\)
对于单点修改和区间修改中未被完全包含在块内的部分,就先下传 \(Lazy\) 标记,再暴力进行更新,复杂度为 \(O(\sqrt{n})\)
如果需要区间查询,可以不断维护每个区间的整体信息,询问中被完全包含的区间就 \(O(1)\) 处理,余下的区域就 \(O(\sqrt{n})\) 暴力查询
总之,大段维护,局部朴素
复制一个与输入的 \(a\) 数组相同的 \(b\) 数组,并对 \(b\) 进行分块,将每一块中的数字排序
修改时,将被包含的完整区间的 \(Lazy\) 加上 \(c\),剩余的部分则暴力更新 \(a\) 数组,更新完后再更新所在段的 \(b\) 数组
修改时,在被包含的完整区间的 \(b\) 数组中二分查找小于 \(c^2-Lazy\) 的数字个数,剩余的部分则遍历 \(a\) 数组,加上其中小于 \(c^2-Lazy\) 的数字个数
2. 莫队算法
一种离线的区间询问算法
如果从 \([l,r]\) 的答案能够 \(O(1)\) 扩展到 \([l-1,r],[l+1,r],[l,r+1],[l,r-1]\)(即与 \([l,r]\) 相邻的区间)的答案,那么可以在 \(O(n\sqrt{n})\) 的复杂度内求出所有询问的答案
将每个询问的区间的左端点对应 \(x\) 坐标,右端点对应 \(y\) 坐标,那么,所有的询问就可以抽象为平面直角坐标系上的坐标点,区间转移所需要的扩展次数就等于坐标系上两个坐标点的曼哈顿距离,改变每个询问的遍历顺序就可以优化时间复杂度
莫队算法先将数列分为 \(\sqrt{n}\) 块,对于每个询问,先按照左端点所在块排序,再按右端点排序,依次进行处理
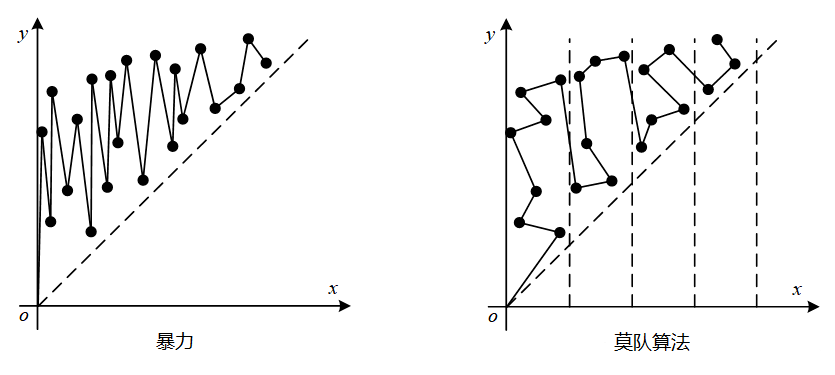
左端点在一个分块中时,右端点一直向右移动,一共最多移动 \(n\) 格;左端点在块内最多移动 \(\sqrt{n}\) 次,每次最多移动 \(\sqrt{n}\) 格,一共最多移动 \(n\) 格
而一共有 \(\sqrt{n}\) 个这样的分块,所以总时间复杂度为 \(O(n \sqrt{n})\)
3. 带修改莫队
普通的莫队算法是不支持修改操作的,所以我们需要在每个询问的左端点和右端点以外加上时间维, 表示这次操作是在第几次修改操作后进行的
进行转移的时候也可以在时间维上移动,转移时间复杂度也是 \(O(1)\) 的
将块长设定为 \(n ^ {\frac{2}{3}}\),排序时第一关键字为左端点所在块,第二关键字为右端点所在块,第三关键字为时间,总时间复杂度为 \(O(n ^ \frac{5}{3})\)
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
const int maxn = 2e6 + 10;
int n, m, s, l;
int a[maxn];
struct node1 { int l, r, id, t; } ask[maxn];
struct node2 { int p, Old, New; } change[maxn];
bool cmp(node1 a, node1 b)
{
if ((a.l - 1) / s + 1 != (b.l - 1) / s + 1) return (a.l - 1) / s + 1 < (b.l - 1) / s + 1;
else if ((a.r - 1) / s + 1 != (b.r - 1) / s + 1) return (a.r - 1) / s + 1 < (b.r - 1) / s + 1;
else return a.t < b.t; //注意这里不能写<=
}
int cnt[maxn], tot = 0;
void add(int p) { if (++cnt[a[p]] == 1) tot++; }
void del(int p) { if (--cnt[a[p]] == 0) tot--; }
void modify(int p, int x, int l, int r)
{
if (l <= p && p <= r) del(p);
a[p] = x;
if (l <= p && p <= r) add(p);
}
int ans[maxn];
int main()
{
scanf("%d %d", &n, &m);
s = pow(n, 2.0 / 3.0);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
int cnt1 = 0, cnt2 = 0;
for (int k = 1; k <= m; k++)
{
char str[5]; int x, y;
scanf("%s", &str[1]);
scanf("%d %d", &x, &y);
if (str[1] == 'Q')
{
cnt1++;
ask[cnt1].l = x, ask[cnt1].r = y, ask[cnt1].id = cnt1, ask[cnt1].t = cnt2;
}
else
{
cnt2++;
change[cnt2].p = x, change[cnt2].Old = a[x], change[cnt2].New = y;
a[x] = y;
}
}
sort(ask + 1, ask + cnt1 + 1, cmp);
int L = 1, R = 0, T = cnt2;
for (int i = 1; i <= cnt1; i++)
{
while (L > ask[i].l) add(--L);
while (L < ask[i].l) del(L++);
while (R > ask[i].r) del(R--);
while (R < ask[i].r) add(++R);
while (T > ask[i].t) modify(change[T].p, change[T].Old, L, R), T--;
while (T < ask[i].t) T++, modify(change[T].p, change[T].New, L, R);
ans[ask[i].id] = tot;
}
for (int i = 1; i <= cnt1; i++) printf("%d\n", ans[i]);
return 0;
}
4. 根号分治
和分块没什么关系,主要是他复杂度带根号
如果题目中一共要进行 \(n\) 次操作,所有的操作可以被划分为两类,一种可以用 \(O(\sqrt{n})\) 的时间复杂度解决;另一种时间复杂度 \(O(n)\),但最多会进行 \(\sqrt{n}\) 次,那么,两种情况分别进行处理,整体的时间复杂度就是 \(O(n \times \sqrt{n})\)
5. 整数分块
对于 \(g(x) = \lfloor \frac n x \rfloor\) (其中 \(x\) 为正整数,且 \(1 \le x \le n\)),则 \(g(x)\) 不同值的个数不会超过 \(2\sqrt n\) 个。
$$\Huge\textbf{\color{black}{矩阵}}$$
1. 矩阵
一个 \(n \times m\) 的矩阵可以看做一个 \(n\) 行 \(m\) 列的二维数组
设 \(A\) 是 \(n \times m\) 矩阵,\(B\) 是 \(n \times m\) 矩阵,则 \(C = A + B\) 是 \(n \times m\) 矩阵,且 \(\forall i \in [1,n], \forall j \in [1,m], C_{i,j} = A_{i,j} + B_{i,j}\)
设 \(A\) 是 \(n \times m\) 矩阵,\(B\) 是 \(m \times p\) 矩阵,则 \(C = A \times B\) 是 \(n \times p\) 矩阵,且 \(\forall i \in [1,n], \forall j \in [1,p], C_{i,j} = \sum_{k=1}^{m} A_{i,k} \times B_{k,j}\)
简而言之,矩阵加法就是将每个位置上的数对应相加,矩阵乘法中 \(C\) 矩阵第 \(i\) 行 \(j\) 列就等于 \(A\) 矩阵第 \(i\) 行和 \(B\) 矩阵第 \(j\) 列上的数分别相乘再相加
矩阵乘法不满足交换律,但满足结合律和分配率,因此我们可以使用类似整数快速幂的方式进行矩阵快速幂
struct matrix
{
int n, m;
long long a[maxn][maxn];
matrix(int _n, int _m)
{
n = _n, m = _m;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
a[i][j] = 0;
}
matrix operator * (const matrix& t) const
{
assert(m == t.n);
matrix ans(n, t.m);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= t.m; j++)
for (int k = 1; k <= m; k++)
ans.a[i][j] = (ans.a[i][j] + a[i][k] * t.a[k][j]) % mod;
return ans;
}
matrix operator + (const matrix& t) const
{
assert(n == t.n && m == t.m);
matrix ans(n, m);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
ans.a[i][j] = (a[i][j] + t.a[i][j]) % mod;
return ans;
}
matrix operator ^ (const long long& t) const
{
matrix x(n, m);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
x.a[i][j] = a[i][j];
long long p = t;
matrix ans(n, m);
for (int i = 1; i <= ans.n; i++) ans.a[i][i] = 1;
while (p)
{
if (p & 1) ans = ans * x;
p >>= 1;
x = x * x;
}
return ans;
}
void print()
{
printf("\nn = %d, m = %d\n", n, m);
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++) printf("%lld ", a[i][j]);
printf("\n");
}
printf("\n");
}
};
2.矩阵快速幂加速递推
若数列 \(f\) 存在线性递推公式,即
\(f_i = a_i \text{,其中} i \leq k\)
\(f_i = \sum_{j=1}^{k} b_j \times f_{i-k+j-1} \text{,其中} i > k\)
那么我们就可以通过矩阵快速幂加速对 \(f\) 的递推
构造矩阵 \(A, B, C\)
$ A =
\begin{bmatrix}
a_1 & a_2 & a_3 & ... & a_k
\end{bmatrix}
$
$ B =
\begin{bmatrix}
0 & 0 & 0 & \cdots & 0 & 0 & b_1\
1 & 0 & 0 & \cdots & 0 & 0 & b_2\
0 & 1 & 0 & \cdots & 0 & 0 & b_3\
0 & 0 & 1 & \cdots & 0 & 0 & b_4\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots\
0 & 0 & 0 & \cdots & 1 & 0 & b_{k-1}\
0 & 0 & 0 & \cdots & 0 & 1 & b_k
\end{bmatrix}
$
\(C = A \times B ^{n - k}\)
\(C_{1,k}\) 即为 \(f_n\) 的值,使用矩阵快速幂,时间复杂度为 \(O(\log n \times k ^ 3)\)
标签:总结,二分,int,暑期,dfn,maxn,low,节点 From: https://www.cnblogs.com/wxr-blog/p/17923532.html
