The backtracking solutions of most leetcode-problems have a similar pattern. Let's take a look on it.
Subset
1. Recursion (Backtrack) - Time complexity is O(2^n), and the depth of recursion is O(n).
class Solution {
public:
vector<vector<int>> ret;
vector<int> sub;
int n;
vector<vector<int>> subsets(vector<int>& nums)
{
n = nums.size();
backtrack(nums, 0);
return ret;
}
void backtrack(vector<int>& nums, int idx)
{
ret.emplace_back(sub);
for (int i = idx; i < n; ++i)
{
sub.emplace_back(nums[i]);
backtrack(nums, i + 1);
sub.pop_back();
}
}
};
2. Iteration - Time complexity is still O(2^n), while space complexity is O(1).
For example, if nums = [1, 2, 3], then the changing process of subs is:
init : {[]}
x = 1 : {[], [1]}
x = 2 : {[], [1], [2], [1, 2]}
x = 3 : {[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]}
Our code:
class Solution {
public:
vector<vector<int>> subsets(vector<int>& nums) {
vector<vector<int>> subs = {{}};
for (int x : nums)
{
int n = subs.size();
for (int i = 0; i < n; i++)
{
subs.emplace_back(subs[i]);
subs.back().emplace_back(x);
}
}
return subs;
}
};
3. bitmap - Here the time complexity is O(2^N * N).
class Solution {
public:
vector<vector<int>> subsets(vector<int>& nums)
{
int n = nums.size();
int total = 1 << n;
vector<vector<int>> subs(total);
for (int i = 0; i < total; ++i)
{
for (int j = 0; j < n; ++j)
if ((i >> j) & 1) subs[i].emplace_back(nums[j]);
}
return subs;
}
};
Subset II
1. Backtrack (recursion) - It's similar to "Subset" above.
class Solution {
public:
int n;
vector<vector<int>> ret;
vector<int> sub;
vector<vector<int>> subsetsWithDup(vector<int>& nums)
{
sort(nums.begin(), nums.end());
n = nums.size();
backtrack(nums, 0);
return ret;
}
void backtrack(vector<int> &nums, int idx)
{
ret.emplace_back(sub);
for (int i = idx; i < n; ++i)
{
if (i > idx && nums[i] == nums[i - 1]) continue;
sub.emplace_back(nums[i]);
backtrack(nums, i + 1);
sub.pop_back();
}
}
};
2. Iteration
It's a little similar to "Subset - Iteration" above, but not totally. See this explanation.
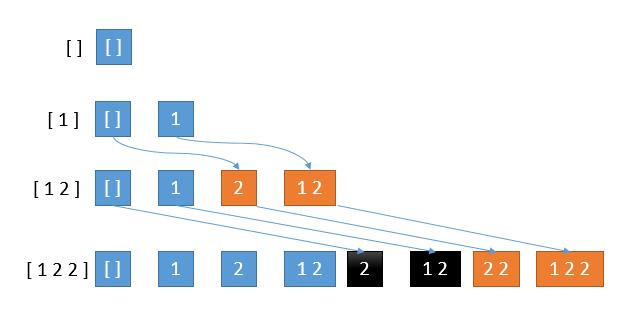
For "Interation Solution" of Subset, in the internal loop, we traverse all elements in the subs. Here we can not do so, since there are duplicate numbers.
As the figure shown above, if we still traverse all elements of subs, then we will add duplicate subsets into subs (the black ones). We need to fix this issue.
When we meet the duplicate number, such as second 2 above, we should not traverse all elements of subs. We just need to traverse the newest added ones (the orange elements in 3rd line).
Here we use variable start to store start-position of the newest elements.
class Solution {
public:
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
sort(nums.begin(), nums.end());
vector<vector<int>> subs = {{}};
int size = nums.size();
int start = subs.size();
for (int i = 0; i < size; ++i)
{
int n = subs.size();
for (int j = 0; j < n; ++j)
{
if ((i > 0 && nums[i] == nums[i - 1]) && j < start)
continue;
subs.emplace_back(subs[j]);
subs.back().emplace_back(nums[i]);
}
start = n;
}
return subs;
}
};
Permutations
1. Backtrack
- We allocate a buffer
seq, to store each permutation ofnums. - For each position of
seq[idx], we try to put every numbersnums[i]on it (unlessnums[i]have been used) . - Note that in the for-loop of backtrack function, we do not start at
idx, while start at0.- Why is it different from "Subset"? From the perspective of consequence, Subset has
2^ndifferent states, while permutation hasn!different states. The actual reason is that here each number must occur at least once inseq, while the situation in Subset is not.
- Why is it different from "Subset"? From the perspective of consequence, Subset has
class Solution {
public:
vector<vector<int>> ret;
vector<int> seq;
bool used[6] = {0};
int n;
vector<vector<int>> permute(vector<int>& nums) {
n = nums.size();
seq.resize(n);
backtrack(nums, 0);
return ret;
}
void backtrack(vector<int> &nums, int idx)
{
if (idx >= n)
{
ret.emplace_back(seq);
return;
}
// here we do not start from idx
// for position seq[idx], we try to put each number on it
for (int i = 0; i < n; ++i)
{
if (used[i]) continue;
seq[idx] = nums[i], used[i] = true;
backtrack(nums, idx + 1);
used[i] = false;
}
}
};
Permutation II
1. Backtrack
There are duplicate number, hence we need a little modification on the solution of "Permutations".
See the if-branch, we add a new skip condition (i > 0 && nums[i] == nums[i - 1] && used[i - 1]) .
For example, if input [1a, 1b, a]
seq used idx comment
[1a] [1 0 0] 0
[1a 1b] [1 1 0] 1 (this can not happend, step back)
[1b] [0 1 0] 0
[1b 1a] [1 1 0] 1 (this can happen)
[1b 1a 2a] [1 1 1] 2 (add seq into result)
Thus, we can also change the condition into (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) . It will put 1a on the 1st position in above example.
class Solution {
public:
int n;
vector<int> seq;
vector<vector<int>> res;
bool used[8] = {false};
vector<vector<int>> permuteUnique(vector<int>& nums)
{
sort(nums.begin(), nums.end());
n = nums.size();
seq.resize(n);
backtrack(nums, 0);
return res;
}
void backtrack(vector<int> &nums, int idx)
{
if (idx >= n)
{
res.emplace_back(seq);
return;
}
for (int i = 0; i < n; ++i)
{
if (used[i] || (i > 0 && nums[i] == nums[i - 1] && used[i - 1])) continue;
seq[idx] = nums[i], used[i] = true;
backtrack(nums, idx + 1);
used[i] = false;
}
}
};
Combination Sum
1. Backtracking
class Solution {
public:
vector<vector<int>> res;
vector<int> seq;
int n, target;
vector<vector<int>> combinationSum(vector<int>& nums, int target) {
n = nums.size(), this->target = target;
backtrack(nums, 0, 0);
return res;
}
void backtrack(vector<int> &nums, int idx, int cur)
{
if (cur > target) return;
if (cur == target)
{
res.emplace_back(seq);
return;
}
for (int i = idx; i < n; ++i)
{
seq.emplace_back(nums[i]);
backtrack(nums, i, cur + nums[i]);
seq.pop_back();
}
}
};
Combination Sum II
1. Backtracking
- Sort the
nums - If we meet the same value, then skip it. (See the if-branch below. )
class Solution {
public:
vector<vector<int>> res;
vector<int> seq;
int n, target;
vector<vector<int>> combinationSum2(vector<int>& nums, int target)
{
sort(nums.begin(), nums.end());
n = nums.size(), this->target = target;
backtrack(nums, 0, 0);
return res;
}
void backtrack(vector<int> &nums, int idx, int cur)
{
if (cur > target) return;
if (cur == target)
{
res.emplace_back(seq);
return;
}
for (int i = idx; i < n; ++i)
{
if (i > idx && nums[i] == nums[i - 1]) continue;
seq.emplace_back(nums[i]);
backtrack(nums, i + 1 , cur + nums[i]);
seq.pop_back();
}
}
};
Palindrome Partitioning
1. Backtracking
Time complexity is O(n * 2^n), since for each letter range from 0 to n-1, we have two choices (split it or not), and for each choice, we need to check whether if it is palindrome in O(n) time.
class Solution {
public:
vector<vector<string>> res;
vector<string> buf;
int n;
vector<vector<string>> partition(string s)
{
n = s.length();
backtrack(s, 0);
return res;
}
void backtrack(string &s, int idx)
{
if (idx >= n)
{
res.emplace_back(buf);
return;
}
for (int i = idx; i < n; ++i)
{
if (check(s, idx, i))
{
buf.emplace_back(s.substr(idx, i - idx + 1));
backtrack(s, i + 1);
buf.pop_back();
}
}
}
bool check(string &s, int start, int end)
{
while (start < end)
{
if (s[start] != s[end]) return false;
start++, end--;
}
return true;
}
};
2. Dynamic Programming Optimization
We can pre-process for each postion pair <i, j>, store the result whether if s[i - j] is palindrome in array dp. Hence we can optimize check() method above into O(1) time.
Are the time complexity of this solution O(2^n) ? The answer is NO. See the internal function call s.substr, which need O(n) time. Hence the time complexity here is still O(n * 2 ^ n).
class Solution {
public:
vector<vector<string>> res;
vector<string> buf;
vector<vector<bool>> dp;
int n;
vector<vector<string>> partition(string s) {
n = s.length();
dp.resize(n, vector<bool>(n, true)); // an empty string is always palindrome
for (int i = n - 1; i >= 0; --i)
{
dp[i][i] = true;
for (int j = i + 1; j < n; ++j)
dp[i][j] = s[i] == s[j] && dp[i + 1][j - 1];
}
backtrack(s, 0);
return res;
}
void backtrack(string &s, int idx)
{
if (idx >= n)
{
res.emplace_back(buf);
return;
}
for (int i = idx; i < n; ++i)
{
if (dp[idx][i])
{
buf.emplace_back(s.substr(idx, i - idx + 1));
backtrack(s, i + 1);
buf.pop_back();
}
}
}
};
// dp[i, j] = dp[i+1, j-1] && s[i] == s[j] (j > i)
3. Memor Search
Based on the "backtracking" solution above, we just change the check method into:
unordered_map<int, unordered_map<int, bool>> table;
bool check(string &s, int start, int end)
{
if (start >= end) return true;
if (table.count(start) && table[start].count(end)) return table[start][end];
return table[start][end] = (s[start] == s[end]) && check(s, start + 1, end - 1);
}
N-Queens
1. Backtracking (Recursion)
We assume that each queen is on different rows, and pos[i] denote her column-index of the board. i.e. <i, pos[i]> means the i-th queen is on i-th row, pos[i]-th column.
class Solution {
public:
vector<vector<string>> res;
vector<int> pos;
int n;
vector<vector<string>> solveNQueens(int n)
{
this->n = n;
pos.resize(n, -1);
backtrack(0);
return res;
}
void backtrack(int idx)
{
if (idx >= n)
{
res.emplace_back(generate(pos));
return;
}
for (int i = 0; i < n; ++i)
{
pos[idx] = i;
if (check(idx)) backtrack(idx + 1); // pay attention to this idx + 1
}
}
bool check(int idx)
{
for (int i = 0; i < idx; ++i)
if (pos[idx] == pos[i] || idx - i == abs(pos[idx] - pos[i]))
return false;
return true;
}
vector<string> generate(vector<int> &pos)
{
vector<string> ret(n, string(n, '.'));
for (int i = 0; i < n; i++)
ret[i][pos[i]] = 'Q';
return move(ret);
}
};
2. Iteration
class Solution {
public:
vector<vector<string>> res;
vector<int> pos;
vector<vector<string>> solveNQueens(int n)
{
pos.resize(n, -1);
int cur = 0;
while (cur >= 0)
{
while (pos[cur] < n)
{
if (++pos[cur] >= n) break; // for current queen, try every column
if (check(cur))
{
if (cur < n - 1) ++cur; // not a completed solution
else if (cur == n - 1)
{
res.emplace_back(generate(pos, n));
break;
}
}
}
pos[cur] = -1, cur--;
}
return res;
}
bool check(int idx)
{
for (int i = 0; i < idx; ++i)
if (pos[idx] == pos[i] || idx - i == abs(pos[idx] - pos[i]))
return false;
return true;
}
vector<string> generate(vector<int> &pos, int n)
{
vector<string> ret(n, string(n, '.'));
for (int i = 0; i < n; i++)
ret[i][pos[i]] = 'Q';
return move(ret);
}
};
N-Queens II
1. Iteration
It's an easy problem if we have solve the "N-Queens" with iteration solution.
class Solution {
public:
int totalNQueens(int n) {
vector<int> pos(n, -1);
int cur = 0, res = 0;
while (cur >= 0)
{
while (pos[cur] < n)
{
if (++pos[cur] >= n) break;
if (check(pos, cur))
{
if (cur < n - 1) ++cur;
else
{
++res;
break;
}
}
}
pos[cur--] = -1;
}
return res;
}
bool check(vector<int> &pos, int idx)
{
for (int i = 0; i < idx; ++i)
if (pos[i] == -1 || pos[i] == pos[idx] || idx - i == abs(pos[idx] - pos[i]))
return false;
return true;
}
};
2. backtracking
class Solution {
public:
vector<int> pos;
int n, res;
int totalNQueens(int n)
{
pos.resize(n, -1);
this->n = n, this->res = 0;
backtrack(0);
return res;
}
void backtrack(int idx)
{
if (idx >= n)
{
res += 1;
return;
}
for (int i = 0; i < n; ++i)
{
pos[idx] = i;
if (check(idx)) backtrack(idx + 1);
}
}
bool check(int idx)
{
if (idx >= n) return true;
for (int i = 0; i < idx; ++i)
if (pos[i] == pos[idx] || abs(pos[i] - pos[idx]) == idx - i) return false;
return true;
}
};
Summary
We can see that the backtracking (recursion) pattern is similar in these problem.
vector<vector<int>> res;
vector<int> cur;
vector<vector<int>> solution()
{
backtrack(..., 0);
return res;
}
backtrack(..., int idx)
{
if cur is satisfied with some conditions
{
// add current values into final result, and return
}
for (i = idx; i < n; i++) // or for (i = 0; i < n; i++)
{
cur.push_back(value of i) // try each possible value on current position idx, or cur[idx] = i
if (cur is possible) // if cur[idx]/cur.back() maybe a possible solution
backtrack(..., i + 1) // try next one based on current state, or backtrack(..., idx + 1)
cur.pop_back() // pop the value we have tried, or reset cur[idx]
}
}
And there are two issues if we used this code template.
For the 1st issue, please note that, in the for-loop in backtrack, most of times we start from i = idx, while sometimes we start from i = 0 (e.g. the "Permutations" problem and "Permutations II" problem) .
How can we distinguish these two cases? A simple way is that:
- Start from
i = idxwhen the state space isO(2^n)(or equivalent exponential space). - Start from
i = 0when the state space isO(n!).
The 2nd issue is whether to use backtrack(idx + 1) or backtrack(i + 1).
- In some cases, we use
backtrack(i + 1). - In "N-Queens" and "Permutations" problem, we use
backtrack(idx + 1).
Why? This depends on what is the definition of "next possible value".
- For "Subset", "Combination Sum" and "Palindrome Partition", the next posibble value is
nums[i + 1]ors[i + 1], we try to put it into the current state. Herebacktrack(j)means trynums[j]ors[j]. - However, for the "N-Queens" (and "Permutations"), the position
pos[idx], we want to try all the column-index on postionpos[idx]. Therefore, ifpos[0, ..., idx]is a possible solution, we should continue to try onpos[idx + 1]. In "N-Queen",backtrack(j)means we try to put j-th queen on column-index range from0ton-1. - The most distinct (and essential) difference between these two kind of problems is that, a solution of first one is non-fixed length, while the second one is fixed-length. And the argument
idxofbacktrack(idx)have different meanings.
For these two issues, please learn how to distinguish them via passing these homework:
- 77. Combainations
- 216. Combination Sum III
- 22. Generate Parentheses
- 17. Letter Combinations of a Phone Number
- 306. Additive Number
Combinations
This problem is O(n!) state space.
class Solution {
public:
vector<vector<int>> res;
vector<int> seq;
vector<vector<int>> combine(int n, int k)
{
seq.resize(k, -1);
backtrack(0, n, k);
return res;
}
void backtrack(int idx, int n, int k)
{
if (idx >= k)
{
res.emplace_back(seq);
return;
}
for (int i = 1; i <= n; ++i) // O(n!) state space
{
if (idx > 0 && i <= seq[idx - 1]) continue; // the combination pair require increasing order
seq[idx] = i;
backtrack(idx + 1, n, k); // try next position, fixed-length
seq[idx] = -1;
}
}
};
Combination Sum III
The solution of this problem is fixed-length, and it has O(9!) state space.
class Solution {
public:
vector<vector<int>> res;
vector<int> seq;
vector<vector<int>> combinationSum3(int k, int n)
{
seq.resize(k, 0);
backtrack(0, 0, k, n);
return res;
}
void backtrack(int idx, int cur, int k, int n)
{
if (idx >= k)
{
if (cur == n) res.emplace_back(seq);
return;
}
for (int i = 1; i <= 9; ++i)
{
if (idx > 0 && i <= seq[idx - 1]) continue; // the pairs require increasing order
seq[idx] = i;
backtrack(idx + 1, cur + i, k, n);
seq[idx] = 0;
}
}
};
Generate Parentheses
It is totally backtracking template problem, since
- each solution is in fixed-length
2n, and - each position of a solution, has 2 possible values
'('and')'.
class Solution {
public:
vector<string> res;
string seq;
vector<string> generateParenthesis(int n) {
seq.resize(n << 1, ' ');
backtrack(0, n);
return res;
}
void backtrack(int idx, int n)
{
if (idx >= (n << 1))
{
if (check(seq)) res.emplace_back(seq);
return;
}
static const char values[2] = {'(', ')'};
for (char val : values)
{
seq[idx] = val;
backtrack(idx + 1, n);
seq[idx] = ' ';
}
}
bool check(string &s)
{
int cnt = 0;
for (char x : s)
{
cnt += x == '(', cnt -= x == ')';
if (cnt < 0) return false;
}
return cnt == 0;
}
};
Phone Number
Features of this problem: it is fixed-length, and has O(2^n) state space.
class Solution {
public:
const string letters[10] = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
int n;
string seq;
vector<string> res;
vector<string> letterCombinations(string digits)
{
n = digits.size();
if (n == 0) return res;
seq.resize(n, ' ');
backtrack(digits, 0);
return res;
}
void backtrack(string &digits, int idx)
{
if (idx >= n)
{
res.emplace_back(seq);
return;
}
for (char x : letters[digits[idx] - '0'])
{
seq[idx] = x;
backtrack(digits, idx + 1);
seq[idx] = ' ';
}
}
};
Additive Number
class Solution {
public:
vector<string> buf;
bool ret = false;
int n;
bool isAdditiveNumber(string s)
{
n = s.length();
backtrack(s, 0);
return ret;
}
void backtrack(string &s, int idx)
{
if (ret) return;
if (buf.size() >= 3)
{
if (!checkBuffer()) return;
if (idx >= n)
{
ret = true;
return;
}
}
for (int i = idx; i < n; ++i)
{
buf.emplace_back(s.substr(idx, i - idx + 1));
/* the solution for this problem is not fixed-length */
backtrack(s, i + 1);
buf.pop_back();
}
}
bool checkBuffer()
{
int n = buf.size();
string &a = buf[n - 3], &b = buf[n - 2], &c = buf[n - 1];
if (a.length() > 1 && a[0] == '0' ||
b.length() > 1 && b[0] == '0' ||
c.length() > 1 && c[0] == '0') return false;
return bigIntegerAdd(a, b) == c;
}
string bigIntegerAdd(const string &a, const string &b)
{
int alen = a.length(), blen = b.length();
string res(max(alen, blen) + 1, '0');
int i = alen - 1, j = blen - 1, val = 0, carry = 0;
int ptr = res.length() - 1;
while (i >= 0 || j >= 0)
{
val = carry;
if (i >= 0) val += (a[i--] - '0');
if (j >= 0) val += (b[j--] - '0');
carry = (val >= 10);
val %= 10;
res[ptr--] = val + '0';
}
if (carry) res[ptr--] = 1 + '0';
if (res[0] == '0' && res.length() > 1) res.erase(res.begin());
return res;
}
};