Flood Fill

好习惯：先看样例，直接手模。

手摸完第一个样例我们会发现:

当两个值不一样的连通块相邻时，我们若翻转其中一个，再翻转另外一个的时候，与直接翻转另外一个没有区别。

举个例子：010

我们先翻转 1，变成了 000，此时我们再翻转 000 则变成了 111。

与直接翻转 010 两边的 0 变成 111 没有任何区别。

所以我们大胆猜测将一个连通块变为一个点。

所以知道我们在选择翻转一个连通块的时候不用翻转周围的连通块。

所以显然我们能只翻一个或者都不翻。

问题来了，我们该怎么处理这个？？？

请看下图：

其中 0 的点表示数值为 0 的连通块，1 的点同理。边上的 翻转 表示连通块翻转的话会造成的花费(也就是翻转后 A 图与 B 图不同的点的个数)， 不翻转 同理。

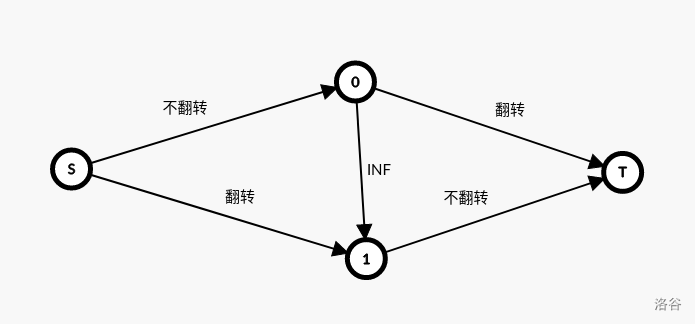
这样就能保证我们的最小割的容量不存在同时翻转的贡献了。

#include <bits/stdc++.h>

int N, M;
int S = 1, T = 2;
int tot = 2, id[1100][1100];
int A[1100][1100], B[1100][1100];
int cnt = 1, head[1100000], next[2100000], to[2100000], value[2100000];

void AddEdge(int u, int v, int val) {
    ++ cnt;
    next[cnt] = head[u];
    head[u] = cnt;
    to[cnt] = v;
    value[cnt] = val;
}

class DisjointSet {
public:
    int fat[1100000];
    int size[1100000];
    int different[1100000]    ;
    void clear() {
        for (int i = 1; i <= N * M + 100; ++ i) {
            fat[i] = i;
            size[i] = 1;
            different[i] = 0;
        }
    }
    int Find(int x) {
        if (fat[x] != x)
            fat[x] = Find(fat[x]);
        return fat[x];
    }
    void Union(int x, int y) {
        x = Find(x);
        y = Find(y);
        if (x != y) {
            fat[x] = y;
            size[y] += size[x];
            different[y] += different[x];
        }
    }
    void Add(int x) {
        x = Find(x);
        different[x] ++;
    }
}set;

std::pair<int, int> origin[1100000];
std::set<std::pair<int, int>> Set;
bool visit[1100000];
int answer;

namespace Dinic {
    int deep[1100000], cur[1100000];
    void clear() {
        for (int i = 1; i <= tot; ++ i) {
            deep[i] = 0;
            cur[i] = head[i];
        }
    }
    bool Bfs(int begin, int end) {
        clear();
        deep[begin] = 1;
        std::queue<int> queue;
        queue.emplace(begin);
        while (queue.size()) {
            int now = queue.front();
            queue.pop();
            for (int i = head[now]; i; i = next[i]) {
                if (!value[i] || deep[to[i]])
                    continue;
                deep[to[i]] = deep[now] + 1;
                if (to[i] == end)
                    return true;
                queue.emplace(to[i]);
            }
        }
        return false;
    }
    int Dfs(int now, int end, int flow) {
        if (now == end)
            return flow;
        int rest = flow, temp;
        for (int i = cur[now]; i && rest; i = next[i]) {
            cur[now] = i;
            if (value[i] && deep[to[i]] == deep[now] + 1) {
                temp = Dfs(to[i], end, std::min(rest, value[i]));
                if (!temp)
                    deep[to[i]] = 0;
                value[i] -= temp;
                value[i ^ 1] += temp;
                rest -= temp;
            }
        }
        return flow - rest;
    }
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);

    std::cin >> N >> M;
    set.clear();
    memset(A, -1, sizeof(A));
    for (int i = 1; i <= N; ++ i) {
        for (int j = 1; j <= M; ++ j) {
            char ch;
            std::cin >> ch;
            A[i][j] = ch - '0';
            id[i][j] = ++ tot;
        }
    }
    for (int i = 1; i <= N; ++ i) {
        for (int j = 1; j <= M; ++ j) {
            char ch;
            std::cin >> ch;
            B[i][j] = ch - '0';
            if (A[i][j] != B[i][j]) 
                set.Add(id[i][j]);
            if (A[i][j] == A[i - 1][j]) 
                set.Union(id[i][j], id[i - 1][j]);
            if (A[i][j] == A[i][j - 1])
                set.Union(id[i][j], id[i][j - 1]);
        }
    }
    for (int i = 1; i <= N; ++ i) {
        for (int j = 1; j <= M; ++ j) {
            int now = set.Find(id[i][j]);
            int different = set.different[now];
            int same = set.size[now] - set.different[now];
            if (!visit[now]) {
                visit[now] = true;
                if (A[i][j] == 0) {
                    AddEdge(S, now, different);
                    AddEdge(now, S, 0);
                    AddEdge(now, T, same);
                    AddEdge(T, now, 0);
                }
                else {
                    AddEdge(S, now, same);
                    AddEdge(now, S, 0);
                    AddEdge(now, T, different);
                    AddEdge(T, now, 0);
                }
            }

            if (A[i][j] + A[i - 1][j] == 1) {
                int x = set.Find(id[i][j]);
                int y = set.Find(id[i - 1][j]);
                if (A[i][j] == 0)
                    Set.emplace(x, y);
                else
                    Set.emplace(y, x);
            }
            if (A[i][j] + A[i][j - 1] == 1) {
                int x = set.Find(id[i][j]);
                int y = set.Find(id[i][j - 1]);
                if (A[i][j] == 0)
                    Set.emplace(x, y);
                else
                    Set.emplace(y, x);
            }
        }
    }
    for (const std::pair<int, int> &iter: Set) {
        AddEdge(iter.first, iter.second, 1e9);
        AddEdge(iter.second, iter.first, 0);
    }
    while (Dinic::Bfs(S, T))
        answer += Dinic::Dfs(S, T, 1e9);
    std::cout << answer << '\n';
    return 0;
}