AcWing 92. 递归实现指数型枚举

题面：从 \(1∼n\) 这 \(n\) 个整数中随机选取任意多个，输出所有可能的选择方案（求子集）。

原题链接：92. 递归实现指数型枚举 - AcWing

目录：

1. 使用dfs树的解法
2. 使用二进制与状态压缩的解法

1. 使用dfs树的解法

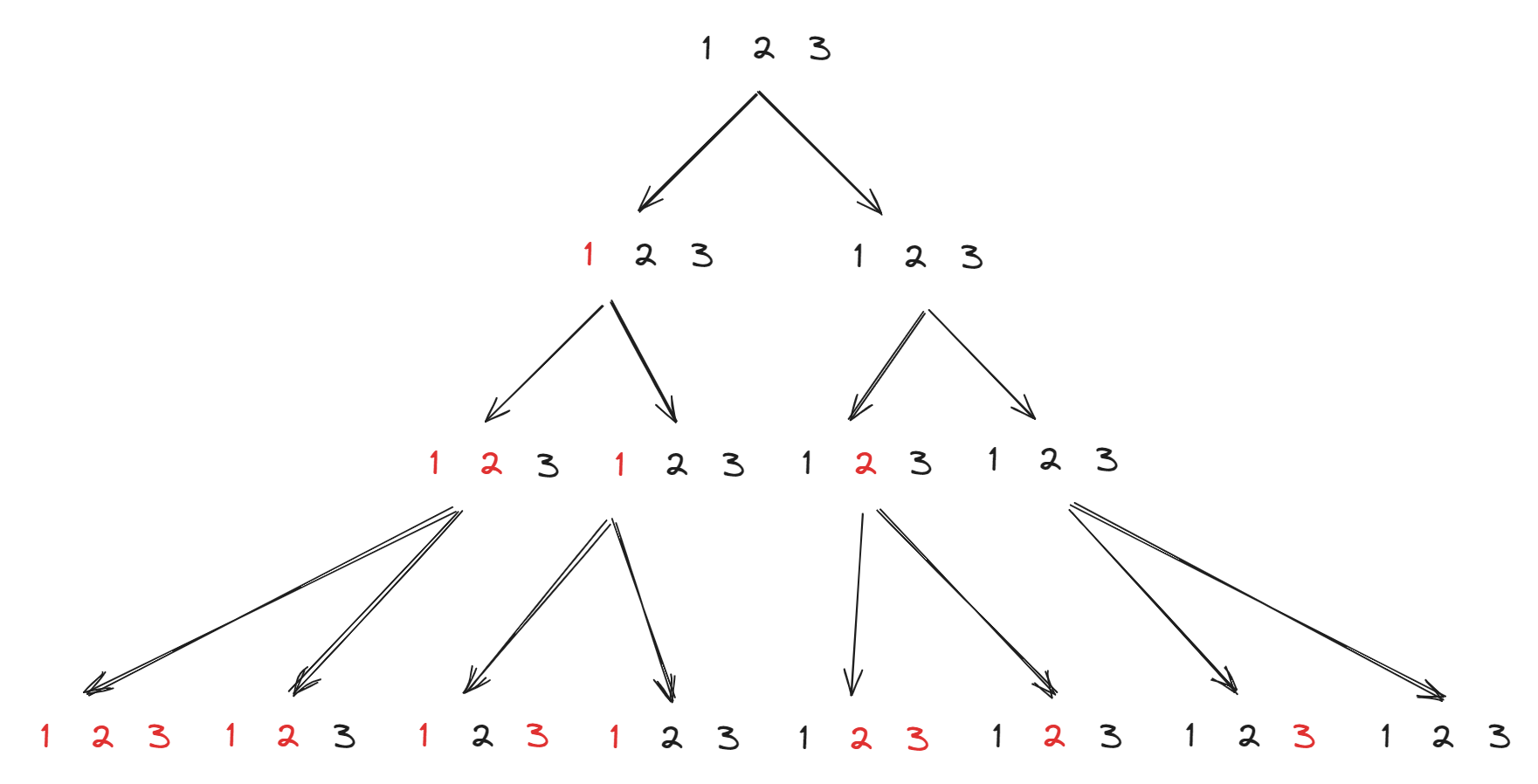
层级既代表递归深度也代表当前数字，左子树为选该层数字，右子树为不选。

#include <bits/stdc++.h>
using namespace std;

const int N = 1010;
int n;
bool st[N];

void dfs(int u) {
	if (u > n) {	//达到最大递归深度
		for (int i = 1; i <= n; i++)
			if (st[i])
				cout << i << " ";	//若该趟中数字被选中，则输出
		cout << endl;
		return;
	}
	//遍历左子树（选）
	st[u] = true;
	dfs(u + 1);
	//遍历右子树（不选）
	st[u] = false;
	dfs(u + 1);
}

int main()
{
	cin >> n;
	dfs(1);
}

2. 使用二进制与状态压缩的解法

为什么要采用二进制？

二进制每一位的0和1可以表示一个二元状态集合；
而二进制本身又表示一个整数，即可以用整数的加减表示状态之间的转移。
压缩：将一个集合压缩成了一个整数（整数作为数组下标）。

位运算的几个注意点：

① 左移乘二，右移除二；
② &与判定是否为1，|异或将该位设为1。

#include <bits/stdc++.h>
using namespace std;

const int N = 1010;
int n;

void dfs(int u, int st) {
	if (u > n) {	//达到最大递归深度
		for (int i = 1; i <= n; i++)
			if (st >> i & 1)	//st的第i位若为1
				cout << i << " ";
		cout << endl;
		return;
	}
	dfs(u + 1, st | 1 << u);	//选，把第u位变成1
	dfs(u + 1, st);				//不选，进入下一步递归
}

int main()
{
	cin >> n;
	dfs(1, 0);
}