Link

ICPC2022Xian L Tree

Question

给出一个根为 \(1\) 的树，需要将树分成几个块每个块，一个块中的节点需要满足以下条件中的一个：

• 对于所有的 \(u,v \in S,\ u \neq v\) ，满足 \(u \in subtree(v)\) 或 \(v \in subtree(u)\)

• 对于所有的 \(u,v \in S,\ u \neq v\) ，满足 \(u \not\in subtree(v)\) 且 \(v \not\in subtree(u)\)

求把树分成的最小块数

Solve

先翻译题目，第一个条件是一条链上的点满足，第二个条件是不同子树上的点满足

只考虑第一种情况，贪心的去想，如果选了 \(x\) ，那么再选一个 \(x\) 的子节点并不会增加块数，那么就尽可能多得去选择，也就是取 \(x\) 往下长的链，那么块数就是长链剖分后的链数

只考虑第二种情况，如果给定一颗树，那么最少的块数就是数最深的节点的深度

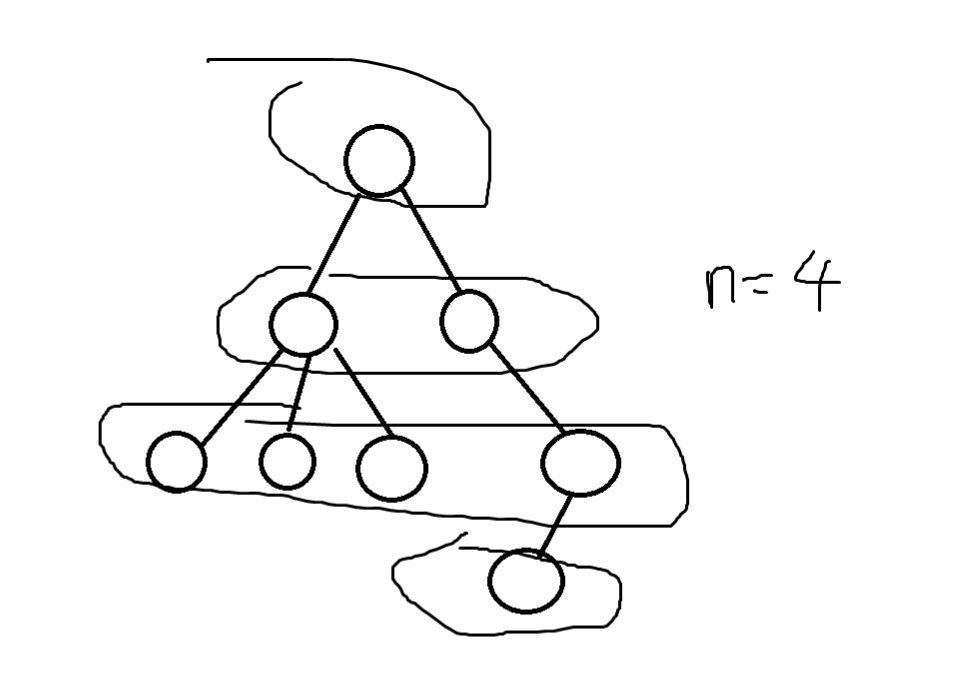
因为假设选了 \(x\) ，那么 \(x\) 的祖先节点就不能和 \(x\) 在一个块里面，所以假设 \(x\) 的深度为 \(dep[x]\) 则，这条链就需要开 \(dep[x]\) 个块，每个块一个节点，对于不同链的节点，把深度相同的放在一个块里面，所以块数就是最深的那个点的深度

对于一颗树，我们从根节点找最长的链，我们发现，最长链的长度就是 \(Max(dep[x])\) ,但由于不知道到底要取多少条链，就枚举链的条数。贪心的想，我们肯定先取长的链，就先预处理出每条链的长度，设为 \(Len_i\) ，假设取了 \(i\) 条链，剩下的节点需要分的块数就是 \(Len_{i+1}\) 所以，总的块数就是 \(i+Len_{i+1}\)，求一个最小值就是答案

Code

#include<bits/stdc++.h>
using namespace std;
inline int read(){
    int ret=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
    while(ch<='9'&&ch>='0')ret=ret*10+ch-'0',ch=getchar();
    return ret*f;
}

const int maxn=1e6+5;
vector<int> dep;
vector<vector<int> > E;
vector<int> son;
vector<int> p;
void dfs1(int x){
    for(auto u: E[x]){
        dfs1(u);
        if(son[x]==0||dep[u]>dep[son[x]]) son[x]=u;
    }
    dep[x]=dep[son[x]]+1;
}
void dfs2(int x,int now_l){
    if(!son[x]) p.push_back(now_l);
    else {
        dfs2(son[x],now_l+1);
        for(auto u:E[x]) {
            if(u!=son[x])
                dfs2(u,1);
        }
    } 
}
inline void solve(){
    int N=read();
    p.clear();
    dep.assign(N+1,0);
    son.assign(N+1,0);
    E.resize(N+1);
    for(auto& x:E){
        x.clear();
    }

    for(int i=2;i<=N;i++){
        int fa=read();
        E[fa].push_back(i);
    }
    dfs1(1);
    dfs2(1,1);
    sort(p.begin(),p.end(),greater<int>());
    int num=p.size(),ans=num;
    for(int i=0;i<num-1;i++){
        int now_ans=i+p[i+1]+1;
        ans=min(now_ans,ans);
    }
    cout<<ans<<endl;
    return ;
}
int main(){
    freopen("L.in","r",stdin);
    int T=read();
    while(T--) solve();
}