Link

UVA11275 3D Triangles

Question

给你三维空间中的两个三角形，请判断它们是否有公共点。

Solution

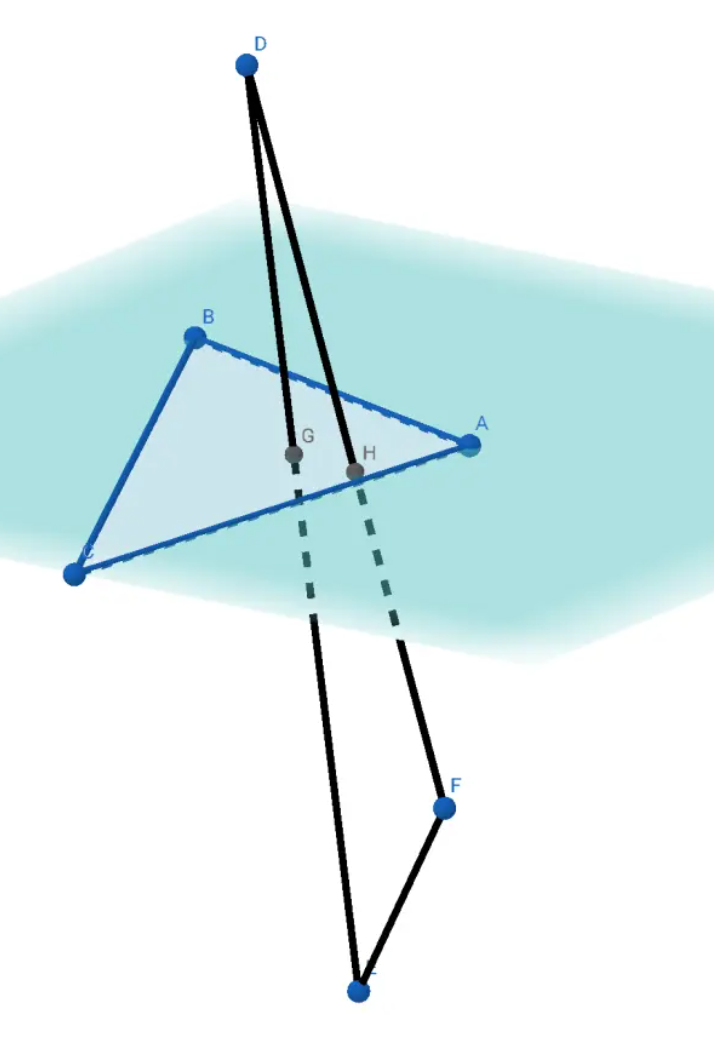
如果在三维空间中相交，那么，肯定有一个三角形的某一条边穿过了另外一个三角形

Code

#include<bits/stdc++.h>
using namespace std;
const double eps=1e-9;
struct Point3{
    double x,y,z;
    Point3(double x=0,double y=0,double z=0):x(x),y(y),z(z){}
};
typedef Point3 Vector3;

Vector3 operator +(Vector3 A,Vector3 B) {return Vector3(A.x+B.x,A.y+B.y,A.z+B.z);}
Vector3 operator -(Point3 A,Point3 B) {return Vector3(A.x-B.x,A.y-B.y,A.z-B.z);}
Vector3 operator *(Vector3 A,double p) {return Vector3(A.x*p,A.y*p,A.z*p);}
Vector3 operator /(Vector3 A,double p) {return Vector3(A.x/p,A.y/p,A.z/p);}
int dcmp(double x){if(fabs(x)<eps) return 0;else return x<0?-1:1;}  //自定义比较函数
bool operator ==(const Point3 &a,const Point3 &b){return dcmp(a.x-b.x)==0 && dcmp(a.y-b.y)==0 && dcmp(a.z-b.z)==0;}
double Dot(Vector3 A,Vector3 B) {return A.x*B.x+A.y*B.y+A.z*B.z;}
double Length(Vector3 A) {return sqrt(Dot(A,A));}
Vector3 Cross(Vector3 A, Vector3 B) {return Vector3(A.y*B.z-A.z*B.y,A.z*B.x-A.x*B.z,A.x*B.y-A.y*B.x);}
double Area2(Point3 A,Point3 B,Point3 C) {return Length(Cross(B-A,C-A));}
bool PointInTri(Point3 P,Point3 P0,Point3 P1,Point3 P2){//点p在▲P0P1P2中
    double area1=Area2(P,P0,P1),area2=Area2(P,P1,P2),area3=Area2(P,P2,P0);
    return dcmp(area1+area2+area3-Area2(P0,P1,P2))==0;
}
Point3 read_point3(){Point3 P;scanf("%lf%lf%lf",&P.x,&P.y,&P.z);return P;}
bool TriSegIntersection(Point3 P0,Point3 P1,Point3 P2,Point3 A,Point3 B,Point3& P){//▲P0P1P2是否和线段AB相交
    Vector3 n=Cross(P1-P0,P2-P0);
    if(dcmp(Dot(n,B-A))==0) return false; //线段 AB 和平面 P0P1P2 平行或共面
    else{
        double t=Dot(n,P0-A)/Dot(n,B-A);
        if(dcmp(t)<0||dcmp(t-1)>0) return false; //交点不在线段AB上
        P=A+(B-A)*t;  //计算交点
        return PointInTri(P,P0,P1,P2);  //判断交点是否在三角形 P0-P1-P2 内
    }
}
bool TriTriIntersection(Point3* T1,Point3* T2){
    Point3 P;
    for(int i=0;i<3;i++){
        if(TriSegIntersection(T1[0],T1[1],T1[2],T2[i],T2[(i+1)%3],P)) return 1;
        if(TriSegIntersection(T2[0],T2[1],T2[2],T1[i],T1[(i+1)%3],P)) return 1;
    }
    return 0;
}
int main(){
    freopen("UVA11257.in","r",stdin);
    int T;
    scanf("%d",&T);
    while(T--){
        Point3 T1[3],T2[3];
        for(int i=0;i<3;i++) T1[i]=read_point3();
        for(int i=0;i<3;i++) T2[i]=read_point3();
        printf("%d\n",TriTriIntersection(T1,T2)?1:0);
    }
    return 0;
}