[IOI2015] Teams 题解

妙妙题。

不难发现，我们对于每个 \(k\) 取出的人都是满足 \(a_i \leq k \leq b_i\) 的。

经典的，我们直接将 \((a_i, b_i)\) 转化到二维平面上，将它转化成一个二维数点问题。

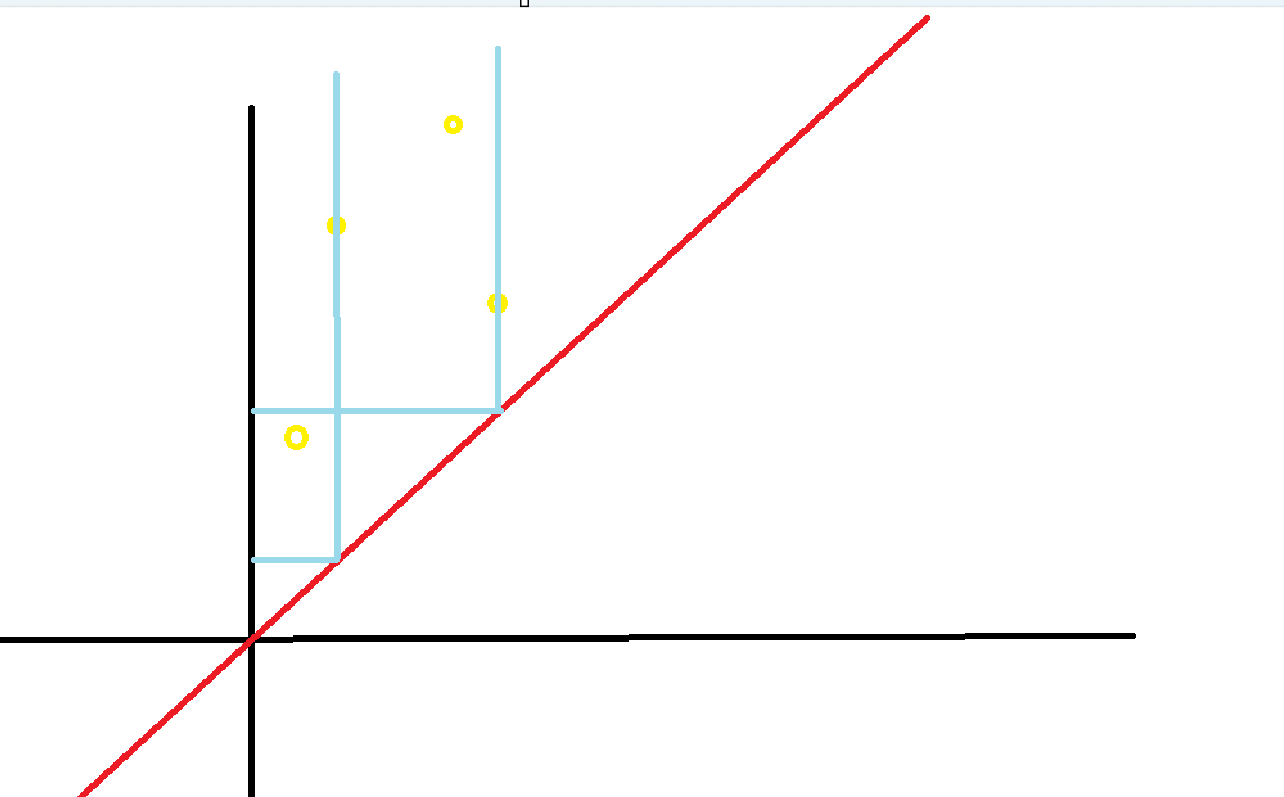
我们对于每一个询问，都使 \(k\) 有序，从小到大贪心的选择，也就相当于 \(x\) 轴限制不断向右，\(y\) 轴限制不断向上。

如果每次的询问 \(m = 1\) 我们直接用主席树二维数点即可，但是如果 \(m > 1\)，有一些点我们前面可能用掉了，后面就不能用了，所以我们考虑怎么维护用掉的点。

我们发现，在贪心的过程中，每一次我们都会选择 \(y\) 轴尽量小的点。

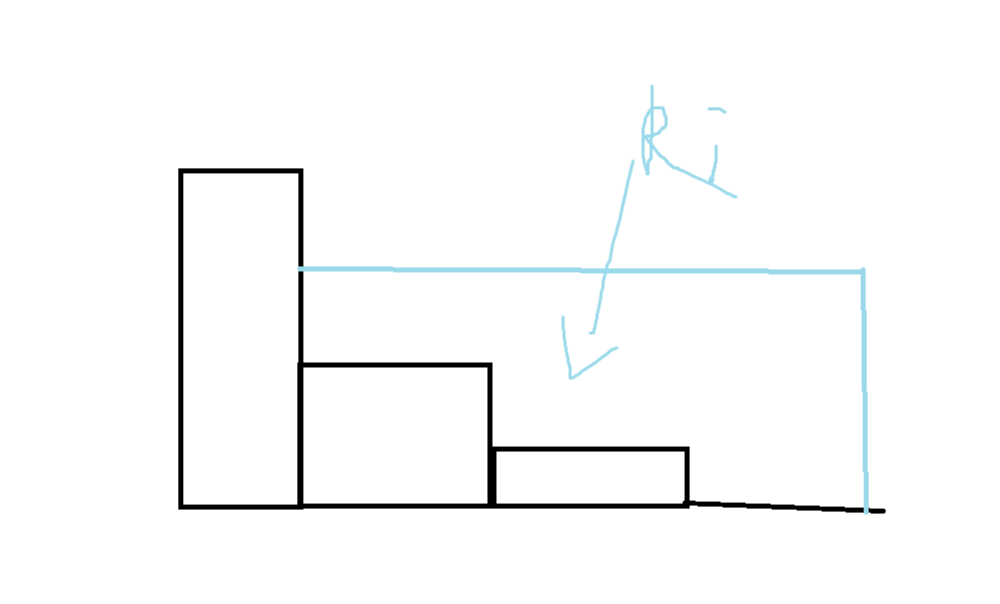
然后我们观察被 \(\rm ban\) 掉的点的范围，发现一定是单调递减的，如图所示，我们新 \(\rm ban\) 掉的点的顶端一定是平衡的。

理解了这些，我们再具体说说细节：

我们记一个数组 \(H\) 为我们当前栈可以被取的点中 \(y\) 最小的那一个，当我们发现 \(H < k_i\) 的时候，我们当前栈顶就失效了，很好理解。

我们再记一个数组 \(q\) 为我们当前总栈剩下多少点可以取。

以及一个数组 \(s\) 为我们当前栈所对应的 \(x\) 轴的范围 \([1, s]\)。

每一次我们通过二分获取 \(H\)，如果当前 \(H\) 比栈顶的 \(H\) 还大，说明我们可以继续平摊。

code:

int n, T;
int a[L], b[L];
vector<int> e[L];
int k[L];

namespace segment_tree {
    #define mid (l + r >> 1)
    #define lson L, R, l, mid, tree[w].l
    #define rson L, R, mid + 1, r, tree[w].r
    int cnt = 0;
    const int L = 4e7 + 5;
    int root[L];
    struct node {
        int l, r, num;
    } tree[L];
    int clone(int w) {
        int nw = ++ cnt;
        tree[nw] = tree[w];
        return nw;
    }
    void pushup(int w) {
        tree[w].num = tree[tree[w].l].num + tree[tree[w].r].num;
    }
    int modify(int L, int R, int l, int r, int w, int num) {
        w = clone(w);
        if(L <= l && r <= R) { tree[w].num ++; return w; }
        if(R <= mid) tree[w].l = modify(lson, num);
        else if(mid < L) tree[w].r = modify(rson, num);
        else tree[w].l = modify(lson, num), tree[w].r = modify(rson, num);
        pushup(w);
        return w;
    }
    int query(int L, int R, int l, int r, int w) {
        if(L <= l && r <= R) return tree[w].num;
        if(R <= mid) return query(lson);
        else if(mid < L) return query(rson);
        else return query(lson) + query(rson);    
    }
    int build(int l, int r, int w) {
        if(l != r)
            tree[w].l = build(l, mid, ++ cnt), tree[w].r = build(mid + 1, r, ++ cnt), pushup(w);
        else
            tree[w].num = 0;
        return w;
    }
}

using segment_tree::build;
using segment_tree::root;
using segment_tree::modify;
using segment_tree::query;
using segment_tree::tree;

int QueryH(int L, int R, int l, int r, int num) {
    if(l == r) return l;
    if(num > tree[tree[R].r].num - tree[tree[L].r].num) return QueryH(tree[L].l, tree[R].l, l, (l + r >> 1), num - (tree[tree[R].r].num - tree[tree[L].r].num));
    else return QueryH(tree[L].r, tree[R].r, (l + r >> 1) + 1, r, num);
}

int s[L], q[L], high[L];

signed main() {
    n = read();
    rep(i, 1, n) {
        a[i] = read(), b[i] = read();
        e[a[i]].push_back(b[i]);
    }
    root[0] = build(1, n, 0);
    rep(i, 1, n) {
        root[i] = root[i - 1];
        for(auto d : e[i]) root[i] = modify(d, d, 1, n, root[i], 1);
    }
    T = read();
    while(T --) {
        int m = read();
        rep(i, 1, m) k[i] = read();
        sort(k + 1, k + 1 + m);
        int Top = 0;
        rep(i, 1, m) {
            while(high[Top] < k[i] && Top) Top --;
            int tot = query(k[i], n, 1, n, root[k[i]]) - query(k[i], n, 1, n, root[s[Top]]) + q[Top] - k[i];
            if(tot < 0) { 
                puts("0"); 
                goto leave; 
            }
            int H = QueryH(root[s[Top]], root[k[i]], 1, n, tot - q[Top]);
            while(high[Top] < H && Top) Top --, H = QueryH(root[s[Top]], root[k[i]], 1, n, tot - q[Top]);
            Top ++;
            s[Top] = k[i], q[Top] = tot, high[Top] = H;
        }
        puts("1");
        leave:;
    }
    return 0;
}