时空乱流

• Problem:E

• Time Limit:1500ms

• Memory Limit:65535K

Description

星际飞行员Alice在一次航行中遭遇了时空乱流，时空乱流将导致Alice乘坐的飞船在n个位面之间穿梭。
星际宇航局管理员Bob收到了Alice的求救信号，决定在某些位面上设立监测站，当Alice进入某个已经设立监测站的位面后，她会立即被拯救。
由于不同位面情况不同，设立监测站的花费也不相同。在第i个位面设立监测站，所需花费为Ci。
时空乱流已经被星际宇航局完全勘测，每个位面都有通往某个位面的通道，如果第i个位面没有监测站，Alice会前往第Ai个位面。（若Ai=i则会停留在当前位面）
Bob并不知道Alice的初始位置，他必须考虑所有可能的情况，并使用尽可能少的花费，确保能从时空乱流中救出Alice。
你能帮Bob计算出至少要花费多少，才能确保能救出Alice吗？`

Input

第一行一个整数T，表示有T组测试数据。
每组测试数据，第一行一个整数n (1≤n≤200000)，表示有n个位面。
第二行n个整数Ci(1≤Ci≤10000)，表示在第i个位面设立监测站的花费Ci。
第三行n个整数Ai(1≤Ai≤n)，表示第i个位面通往第Ai个位面。

Output

每组数据输出一个整数，表示最小花费。

Sample Input

3
5
1 2 3 2 10
1 3 4 3 3
4
1 10 2 10
2 4 2 2
7
1 1 1 1 1 1 1
2 2 2 3 6 7 6

Sample Output

3
10
2

Hint

输入数据较多，请使用scanf/printf

Source

AotoriChiaki

思路

根据题干，可以建出有向图，例如：

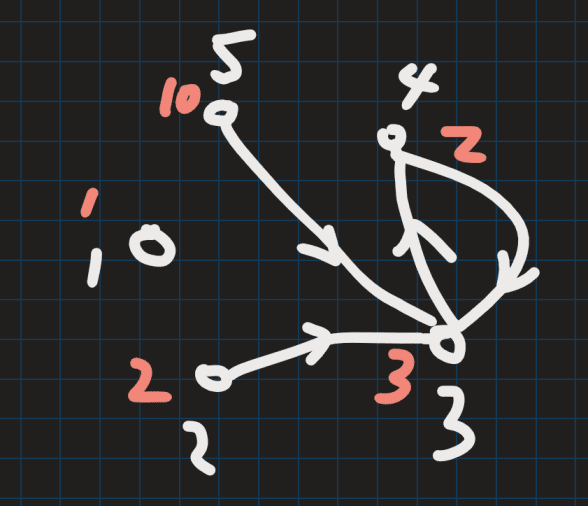
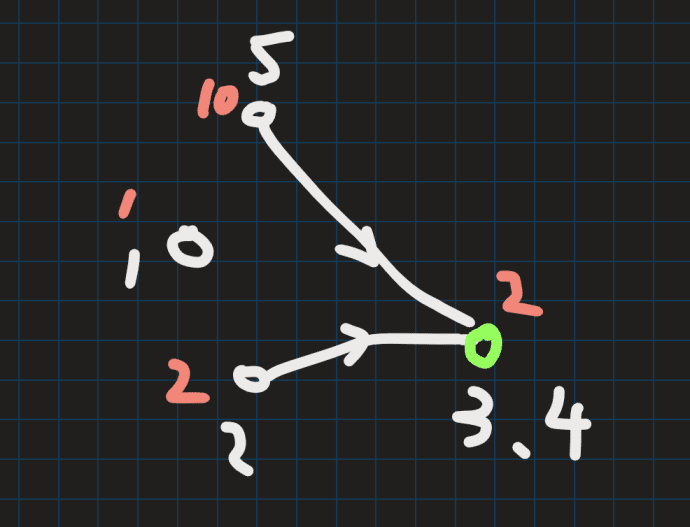
首先分析对于图中所有环，可以缩为一个点，该点的权重等于环上最小权重点

→

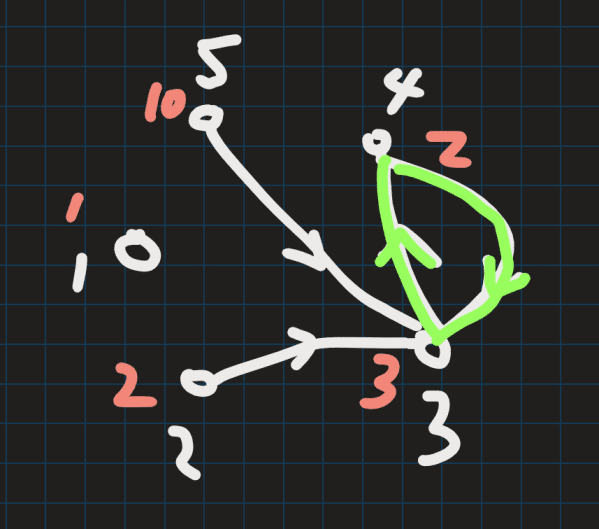然后进行以下分析：

• 如果不在树根建站，则没有任何节点指向树根，则树根处未收录，必须额外在树根建站，所以树根必建站。
• 由于每个连通分量中的每个点都会指向树根，如果在树根建站，即可满足该联通分量每个点被收录。

所以在环缩点后每个树的树根建站即可满足题中条件。

如何实现？

对于缩点前的图：

• 每个点成为树根的条件为入度=0，所以如果有点满足入度为0则可以直接建站。
• 每个环都会被缩成点，所以针对每个环如果环上的点均满足入度为1（环上的点产生的入度），即可在该环上的最小值点建站

使用并查集完成环的查找和记录

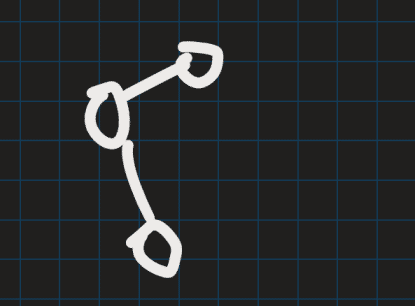
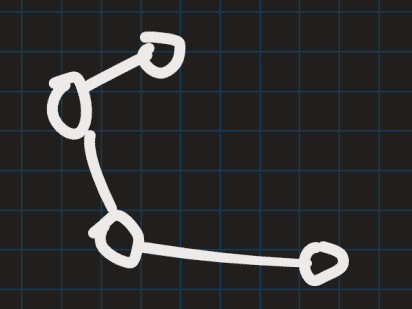
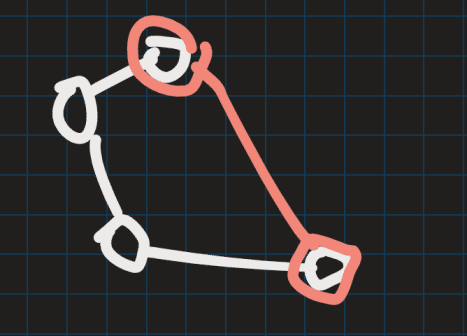
在建图时同时维护一个并查集，如果某边的两端点已经在同一个并查集中（图中红色边），则说明此处有环，只进行记录而不进行并查集合并，可以保证每个环只记录一次。并且这样建成的图是一个树，后续只需要以该边的两端点分别为起点和终点进行dfs即可找到该环的路径。

代码如下

#include <bits/stdc++.h>

using namespace std;

const int N = 2e5+1, INF = 1e9;
const bool _debug = 0;

int c[N], fa[N]; //花费, 并查集父节点
pair<int, int> rnd[N];//环
vector<int> rod[N];//存边

int n;

void Init()
{
    for (int i = 1; i <= n; i ++)
        fa[i] = i;
}
int Find(int x)
{
    if(x == fa[x])
        return x;
    return fa[x] = Find(fa[x]);
}

void Dfs(int t, int goal, stack<int> &path)
{
    if(t == goal || path.top() == goal)
        return;
    if(_debug)cout << "当前 :" << t << endl;
    for (int i = 0; i < rod[t].size(); i ++)
    {
        int x = rod[t][i];
        path.push(x);
        if(_debug)cout << x << " 入栈" << endl;
        Dfs(x,goal,path);
        if(path.top() == goal)
            return;
        if(_debug)cout << path.top() << " 出栈" << endl;
        path.pop();
    }
}

int MinCost(pair<int, int> r)
{
    stack<int> path;
    path.push(r.first);
    Dfs(r.first, r.second, path);
    int res = INF;

    if(_debug)cout << "路径: ";
    while(!path.empty())
    {
        if(_debug)cout << path.top() << " ";
        res = min(res, c[path.top()]);
        path.pop();
    }
    if(_debug)cout << " 最小边： " << res << endl;
    return res;
}

int main()
{
    int T;
    cin >> T;
    while(T--)
    {
        //输入n 以及 花费
        int res = 0, rCnt = 0;
        scanf("%d", &n);

        for (int i = 1; i <= n; i ++)
            rod[i].clear();

        Init();
        for (int i = 1; i <= n; i ++)
            scanf("%d", &c[i]);

        //输入边（顺便找环）
        for (int i = 1; i <= n; i ++)
        {
            int inp;
            scanf("%d", &inp);

            if(inp == i)
            {
                //根节点直接加
                res += c[i];
                if(_debug)printf("res = %d\n", res);
                continue;
            }
            if(Find(i) == Find(inp))
            {
                //存环
                rnd[rCnt].first = i;
                rnd[rCnt].second = inp;
                if(_debug)printf("环：%d %d\n", i, inp);
                rCnt++;
                continue;
            }
            //存边、 合并
            rod[inp].push_back(i);
            fa[i] = inp;
        }

        //遍历环
        for(int i = 0; i < rCnt; i ++)
            res += MinCost(rnd[i]);

        printf("%d\n", res);

    }
    return 0;
}