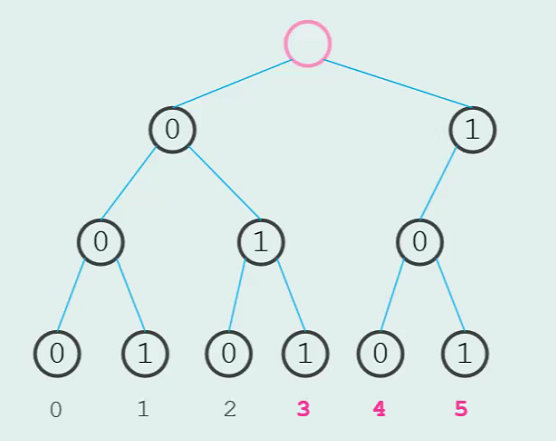
不妨在 Trie 树上考虑这个问题。
首先建一颗树:
这样一来,对于 \(m\) 的限制就自然转化成了只取字典树的前半部分。
先考虑 DP,设 \(f_{u,l,r}\) 表示 \(u\) 号点的子树内取出 \(b\) 数组中下标 \([l,r]\) 的部分。
我们考虑一个节点 \(u\) 向其儿子转移的过程。很自然地,可以得到 \(f_{u,l,r}=\max\limits_{k=l-1}^{r}(f_{ls,l,k}+f_{rs,k+1,r}+a_{k+1}+\dots+a_r)\) 的转移方程。
明显,这里无法枚举所有 Trie 树上的点。但是又发现,同一层上的点除了高位限制以外,本质上是一样的。
所以我们改进一下 DP 数组的定义。\(f_{i,l,r,0/1}\) 表示第 \(i\) 层之下取出 \(b\) 数组中下标 \([l,r]\) 的部分,最后一维表示有无高位限制。按原式计算即可。
据说还可以四边形不等式优化,就看别的奆佬的题解吧(笑。
再仔细一想,发现它竟然和数位 DP 一模一样,其实这本质上是一致的。可是第一眼确实想不太到数位 DP。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=210,M=61;
int n,s[N][N];
ll f[M][N][N][2],a[N],m;
inline ll max(ll x,ll y){
return x>y?x:y;
}
int main(){
memset(f,-0x3f,sizeof f);
scanf("%d%lld",&n,&m);
for(int i=1;i<=n;++i){
scanf("%lld",&a[i]);
a[i]+=a[i-1];
f[0][i][i][0]=f[0][i][i][1]=0;
}
for(int i=0;i<M;++i) for(int j=1;j<=n+1;++j) f[i][j][j-1][0]=f[i][j][j-1][1]=0;
for(int i=1;i<M;++i)
for(int l=1;l<=n;++l)
for(int r=l;r<=n;++r){
if(m&(1ll<<i-1)) for(int k=l-1;k<=r;++k) f[i][l][r][1]=max(f[i][l][r][1],f[i-1][l][k][0]+f[i-1][k+1][r][1]+a[r]-a[k]);
else f[i][l][r][1]=f[i-1][l][r][1];
for(int k=l-1;k<=r;++k) f[i][l][r][0]=max(f[i][l][r][0],f[i-1][l][k][0]+f[i-1][k+1][r][0]+a[r]-a[k]);
}
printf("%lld",f[M-1][1][n][1]);
return 0;
}