分享一种我认为很优美的解法。
首先发现,如果有一个点 \(root\) 使得以它为根,所有叶子深度相等,那么这一定是可行的。可以想象成将它拎出来并且把其他点横向拍扁。
然后,容易发现两个 \(root\) 相同的,满足上面要求的树组合在一起也是可以的,即分成上下两部分分别拍扁。
所以可以想到,如果能找出这个点,那么问题就解决了。
Lemma 1:只要最后能并成一条链,则该链最小长度一定。
Proof:如图,红线,蓝线分别为两种不同答案。
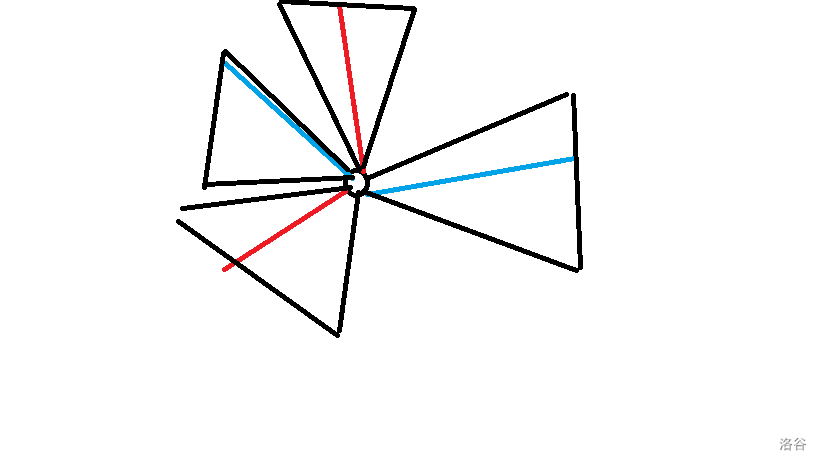
则一定有两段红蓝线对应相等,否则它们将无法合并。
Lemma 2:这个点一定是直径的两个端点之一或直径中点(如果存在)。
Proof:考虑直径在这棵树中的位置。下图中上、下两个三角形代表的子树内叶子深度相同,红线为直径。
- 如果直径跨越两树。
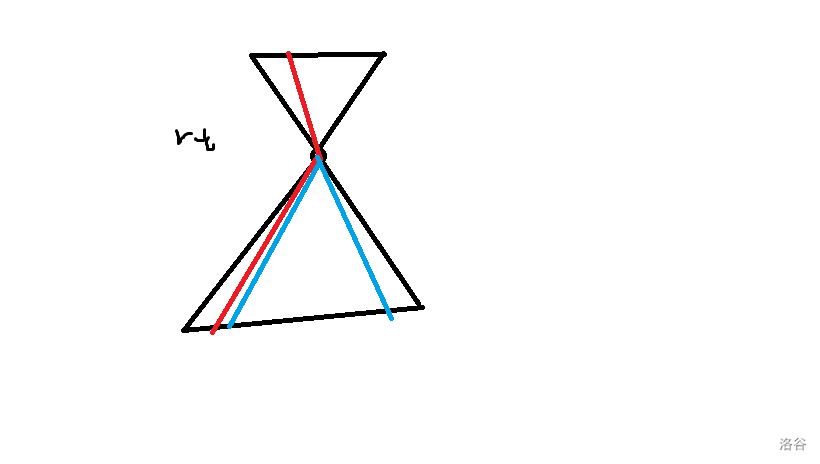
如果有上下有一边只有一棵子树,则一定有一个直径端点可行。
否则,不妨假设下半子树深度大于上半,且 \(root\) 不为直径中点,则一定有蓝线长于红线,则红线不为直径,矛盾。
- 如果直径只在一棵子树内。
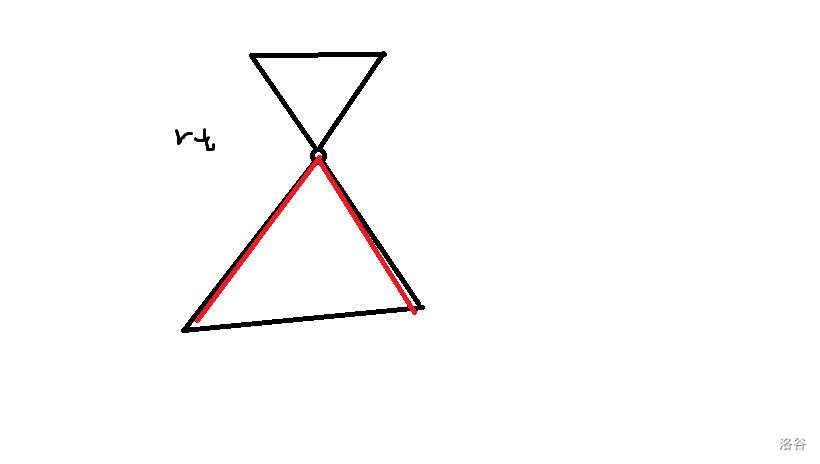
则一定有直径拐点两边长度相等,则 \(root\) 为直径中点。
综上,我们只需要对直径两个端点和中点分别做一遍,即可找到答案。
时间复杂度 \(O(n)\),优于现在有的题解。
code:
点击查看代码
int n,m,t,dep[N],dp[N];
int tot,head[N];
struct node{
int to,nxt;
}e[N<<1];
vector<int> g,d;
il void add(int u,int v){
e[++tot]={v,head[u]};
head[u]=tot;
}
void find_t(int u,int f){
dep[u]=dep[f]+1;
if(dep[u]>dep[t])
t=u;
go(i,u){
int v=e[i].to;
if(v==f)
continue;
find_t(v,u);
}
}
void find_l(int u,int f){
g.eb(u);
if(g.back()==t)return;
go(i,u){
int v=e[i].to;
if(v==f)
continue;
find_l(v,u);
if(g.back()==t)return;
}
g.pop_back();
}
void dfs(int u,int f){
dep[u]=dep[f]+1;
go(i,u){
int v=e[i].to;
if(v==f)
continue;
dfs(v,u);
if(!f){
d.eb(dp[v]);
continue;
}
if(!dp[u])dp[u]=dp[v];
else if(dp[v]!=dp[u])dp[u]=-1;
}
if(!dp[u])dp[u]=dep[u];
}
void solve(int u){
mems(dp,0);
d.clear();
dfs(u,0);
int x=0,y=0;
for(int i:d){
if(i==-1)return;
if(!x)x=i;
else if(x!=i){
if(!y)y=i;
else if(y!=i)return;
}
}
int ans=x&&y?x+y-2:x+y-1;
while(ans%2==0)ans/=2;
printf("%d\n",ans);
exit(0);
}
void Yorushika(){
scanf("%d",&n);
rep(i,1,n-1){
int u,v;
scanf("%d%d",&u,&v);
add(u,v),add(v,u);
}
find_t(1,0);
int x=t;t=0;
find_t(x,0);
int y=t;
find_l(x,0);
solve(x),solve(y);
if(g.size()&1)solve(g[g.size()/2]);
puts("-1");
}
signed main(){
int t=1;
// scanf("%d",&t);
while(t--)
Yorushika();
}