2023-11-04:用go语言,如果n = 1,打印
1***
如果n = 2,打印
1***
3*** 2***
如果n = 3,打印
1***
3*** 2***
4*** 5*** 6***
如果n = 4,打印
1***
3*** 2***
4*** 5*** 6***
10** 9*** 8*** 7***
输入一个数n,表示有多少行,从1开始输出,
奇数行输出奇数个数,奇数行正序,偶数行输出偶数个数,偶数行逆序
每个数后面加*补满四位,中间空4个,第n行顶格输出。
来自华为OD。
来自左程云。
答案2023-11-04:
go代码用灵捷3.5编写,不需要修改。
大体步骤如下:
1.读取输入的整数 n 表示行数。
2.初始化一个大小为 MAXN 的字节数组 space,用于存储打印结果。
3.设置一个布尔变量 from,初始值为 true,用于判断当前是奇数行还是偶数行。
4.进入循环,循环次数为 n:
a.调用 fill 函数,传入 from、当前行的起始值 j、当前行的个数 i 和总列数 m。
b.遍历 space 数组的前 m-4 个元素,打印出空格。
c.打印换行符。
d.将 from 取反,切换到下一行。
5.fill 函数根据 from 的值,分别处理奇数行和偶数行:
a.如果 from 为 true,即当前为奇数行,则从 m-number*8 开始倒序插入 j 个数字,并将起始值 start 自增。
b.如果 from 为 false,即当前为偶数行,则从 m-8 开始顺序插入 j 个数字,并将起始值 start 自增。
6.insert 函数根据当前数 cur 和插入位置 i 的关系,将数字插入到 space 数组中:
a.根据 cur 的位数,计算出数字所占的位数 bit。
b.初始化 offset 为 1。
c.根据计算出的 offset 和 bit,逐个将数字插入到 space 数组中。
d.将剩余位置补充为 *。
最后,根据代码和描述的步骤分析,可以得出以下复杂度:
-
时间复杂度:在循环中,每一次 fill 函数的时间复杂度为 O(n),insert 函数的时间复杂度为 O(1)。因此,总的时间复杂度为 O(n)。
-
空间复杂度:除了输入和输出外,只使用了一个大小为 MAXN 的字节数组 space,因此额外的空间复杂度为 O(MAXN)。
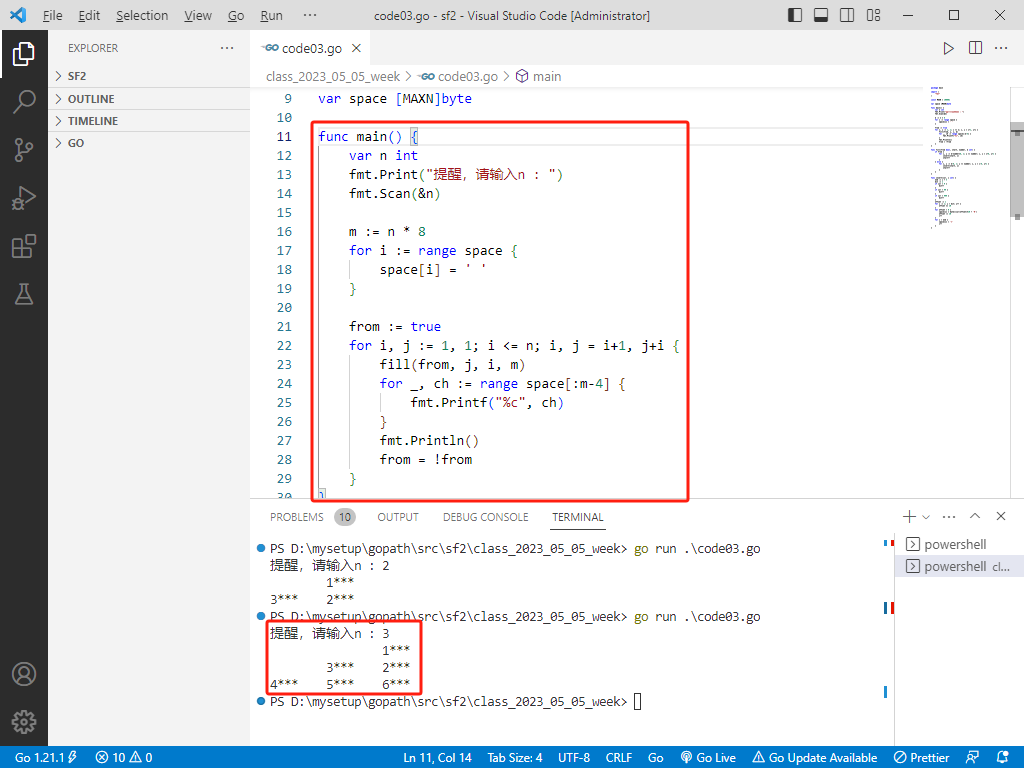
go完整代码如下:
package main
import (
"fmt"
)
const MAXN = 100001
var space [MAXN]byte
func main() {
var n int
fmt.Print("提醒,请输入n : ")
fmt.Scan(&n)
m := n * 8
for i := range space {
space[i] = ' '
}
from := true
for i, j := 1, 1; i <= n; i, j = i+1, j+i {
fill(from, j, i, m)
for _, ch := range space[:m-4] {
fmt.Printf("%c", ch)
}
fmt.Println()
from = !from
}
}
func fill(from bool, start, number, m int) {
if from {
for i, j := m-number*8, 1; j <= number; i, j = i+8, j+1 {
insert(start, i)
start++
}
} else {
for i, j := m-8, 1; j <= number; i, j = i-8, j+1 {
insert(start, i)
start++
}
}
}
func insert(cur, i int) {
end := i + 4
bit := 1
if cur > 9 {
bit++
}
if cur > 99 {
bit++
}
if cur > 999 {
bit++
}
offset := 1
for j := 1; j < bit; j++ {
offset *= 10
}
for offset > 0 {
space[i] = byte((cur/offset)%10 + '0')
offset /= 10
i++
}
for i < end {
space[i] = '*'
i++
}
}