给定 \(n\times m\) 的棋盘,连有横纵 \(2\) 种无向边,有 \(3\) 种类型的边:
- 只允许按照这条边走 \(1\) 步
- 允许继续走边权为 \(2\) 的边,但不允许改变方向
- 允许继续走边权为 \(3\) 的边,可以改变方向
走到不同颜色等级 \(\leq\) 自己等级的棋子时可以吃掉棋子并停下,求先后放下 \(q\) 个棋子时每个棋子最多能走到的位置。
\(n\times m \leq 2\times 10^5,q\leq 10^5\)
感谢这篇博客让我 \(2\) 天做懂了这道神仙题。(写下这篇题解也算是对于 TA 的题解进行补充)
首先肯定会想到维护棋盘上格子的连通性,可以将所有 \(2\) 号道路连成的连续一条(行/列)维护在同一并查集内(所以需要 \(2\) 个并查集),将所有 \(3\) 号道路连成的连通块维护在同一并查集内。然而问题是放上棋子的过程就是断开连通性的过程,实在难以维护,想到的对策是离线所有询问,然后从后往前扫一遍,一边将连通性还原,一边统计答案。
吃子呢?首先 \(1,2\) 号道路好想,只用判断道路末端是否有棋子,若有则判断能否吃掉,如果能吃掉就计入答案。 \(3\) 号道路需要用一个数据结构来维护道路可抵达的所有棋子等级(其实是 \(2\) 个,分别维护 \(2\) 种颜色),然后查询某一连通块内指定颜色的比查询棋子等级小的元素个数(代码中的 \(query1\) )。因为是维护每个并查集,所以还要涉及到合并操作,所以这里选择动态开点权值线段树的合并。
但是仅仅这样统计答案是不行的,比如
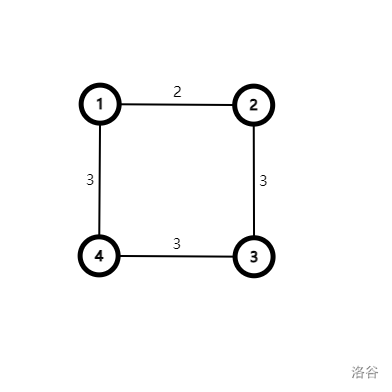
那么 \(1\) 号点就会被算 \(2\) 次。(既在 \(3\) 号并查集内,又在 \(2\) 号横向并查集内)
既然有重复的,那么就判重。利用 \(2\) 号边构成并查集内元素的连续性,可以在并查集中额外加入 \(maxn,minn\) 来得到这一段区间的最大值最小值,然后再额外创建 \(2\) 个线段树来维护横/竖的元素个数,然后可以通过查询区间和来得到被算重的元素个数(实际实现时通过前面提到的查询前缀函数 \(query1(r)-query1(l-1)\) 来实现区间和)。
然后是吃子的问题,所有的 \(1,2\) 道路的吃子都需要查询是否在 \(3\) 道路的吃子中,然而仅凭借等级是无法确定唯一棋子的,所以需要采取一种高级的离散化方法,让所有棋子的等级全部不同而不改变比大小的原则。具体的,让不同等级的棋子依然按照原顺序,而相同等级的棋子按照输入的先后顺序排序,这样之前的棋子就会比之后的棋子小,依然满足比大小的原则,而离散化之后可以通过唯一的等级确定某一棋子是否在线段树内。
最后是一些细节,比如通过用 \(e[i][j]\) 表示标号为 \(j\) 的棋子在 \(i\) 方向上的边权,用 \(val[i]\) 来记录 \(i\) 标号上的点是否有棋子,若有则为输入的顺序,线段树插入时多带一个 \(flag\) ,为 \(1\) 是插入,为 \(-1\) 是删除,还有一些都写在注释里了(震惊,我还会写注释)。
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
#define mp std::make_pair
#define pii std::pair<int,int>
#define chkmin(_A,_B) (_A=std::min(_A,_B))
#define chkmax(_A,_B) (_A=std::max(_A,_B))
int t,n,m;
int e[4][200005],ans[100005],val[200005];
//val用来存储每个点是否有棋子,若有则val[i]表示位置上的点在棋盘上被放上去的顺序(输入的顺序)
//e[i][j]表示编号j的棋子在i方向上的边的权值
int dx[4]={-1,0,1,0};
int dy[4]={0,-1,0,1};
char s[200005];
struct chess{
int col,lv,x,y,id;
}a[100005];
inline bool cmp_lv(const chess &A,const chess &B){return (A.lv==B.lv)?(A.id<B.id):(A.lv<B.lv);}
//等级相同按照来到棋盘上的顺序排序,可以实现相同等级来到棋盘早的可以被来到棋盘晚的吃到
inline bool cmp_id(const chess &A,const chess &B){return A.id<B.id;}
inline int pos1(int x,int y){return (x-1)*m+y;}
inline int pos2(int x,int y){return (y-1)*n+x;}
inline pii getxy(int pos) {return mp((pos-1)/m+1,(pos-1)%m+1);}
void merge_All_ST(int,int);
//--------------------DSU--------------------//
struct DSU{
int f[200005],sz[200005],maxn[200005],minn[200005];
//maxn和minn用于处理同一并查集内元素的最大编号和最小编号
int getfa(const int &x){
return (f[x]==x)?x:f[x]=getfa(f[x]);
}
inline void merge(int x,int y,int flag=0){
x=getfa(x),y=getfa(y);
if(x==y)
return;
if(sz[x]<=sz[y])
std::swap(x,y);
sz[x]+=sz[y];
f[y]=x;
chkmax(maxn[x],maxn[y]);
chkmin(minn[x],minn[y]);
if(flag)
merge_All_ST(x,y);
}
inline void init(const int &p){
for(int i=0;i<=p;++i){
f[i]=maxn[i]=minn[i]=i;
sz[i]=1;
}
}
inline int getmaxn(const int &x){return maxn[getfa(x)];}
inline int getminn(const int &x){return minn[getfa(x)];}
inline int getsize(const int &x){return sz[getfa(x)];}
}dsu[3];
//dsu[0]用来处理类型为3的道路,dsu[1/2]用来处理横竖两个方向的合并情况
//--------------------SegmentTree--------------------//
struct SegmentTree{
struct node{
int ls,rs,sz;
}nd[8000005];
int root[200005],ncnt;
#define ls(_p) (nd[_p].ls)
#define rs(_p) (nd[_p].rs)
void init(){
memset(root,0,sizeof root);
for(int i=0;i<=8000000;++i){
nd[i].ls=nd[i].rs=nd[i].sz=0;
}
ncnt=0;
}
int ins(int p,const int &l,const int &r,const int &x,const int &flag=1){
//flag=1,添加;flag=-1,删除
if(p==0)
p=++ncnt;
if(l==r){
if(flag==-1)
return 0;
if(nd[p].sz==0)
nd[p].sz++;
return p;
}
int mid=(l+r)>>1;
if(x<=mid)
ls(p)=ins(ls(p),l,mid,x,flag);
else
rs(p)=ins(rs(p),mid+1,r,x,flag);
nd[p].sz=nd[ls(p)].sz+nd[rs(p)].sz;
return (nd[p].sz)?p:0;
}
int merge(const int &p,const int &q,const int &l,const int &r){
if(p==0 || q==0)
return p+q;
if(l==r){
nd[p].sz=std::min(nd[p].sz+nd[q].sz,1);
return p;
}
int mid=(l+r)>>1;
ls(p)=merge(ls(p),ls(q),l,mid);
rs(p)=merge(rs(p),rs(q),mid+1,r);
nd[p].sz=nd[ls(p)].sz+nd[rs(p)].sz;
return p;
}
int query1(const int &p,const int &l,const int &r,const int &x){
//查询小于等于某一元素的元素个数
if(p==0 || x==0)
return 0;
if(l==r)
return nd[p].sz;
int mid=(l+r)>>1;
if(x<=mid)
return query1(ls(p),l,mid,x);
else
return nd[ls(p)].sz+query1(rs(p),mid+1,r,x);
}
int query2(const int &p,const int &l,const int &r,const int &x){
//查询某一元素是否在并查集内
if(p==0 || x==0)
return 0;
if(l==r)
return nd[p].sz;
int mid=(l+r)>>1;
if(x<=mid)
return query2(ls(p),l,mid,x);
else
return query2(rs(p),mid+1,r,x);
}
int querynum(const int &p,const int &l,const int &r){
//查询[l,r]内在这一并查集内的元素个数
return query1(root[p],1,n*m,r)-query1(root[p],1,n*m,l-1);
}
}st[4];
//st[0/1]存储等级,st[2/3]存储行/列中的元素个数
int q;
void merge_All_ST(int x,int y){
//将x,y并查集对应的线段树进行合并(并查集是y合并到x,所以线段树也是y合并到x)
st[0].root[x]=st[0].merge(st[0].root[x],st[0].root[y],1,q);
st[1].root[x]=st[1].merge(st[1].root[x],st[1].root[y],1,q);
st[2].root[x]=st[2].merge(st[2].root[x],st[2].root[y],1,n*m);
st[3].root[x]=st[3].merge(st[3].root[x],st[3].root[y],1,n*m);
}
inline bool caneat(const int &x,const int &y){
if(y==0 || y>=x)
return 0;
return (a[x].col!=a[y].col && a[x].lv>=a[y].lv);
}
int main(){
scanf("%d",&t);
while(t--){
scanf("%d %d %d",&n,&m,&q);
memset(e,0,sizeof e);
memset(val,0,sizeof val);
memset(ans,0,sizeof ans);
dsu[0].init(n*m);
dsu[1].init(n*m);
dsu[2].init(n*m);
st[0].init();
st[1].init();
st[2].init();
st[3].init();
for(int i=1;i<=n;++i){
scanf("%s",s+1);
for(int j=1;j<m;++j)
e[1][pos1(i,j+1)]=e[3][pos1(i,j)]=s[j]-'0';
}
for(int i=1;i<n;++i){
scanf("%s",s+1);
for(int j=1;j<=m;++j)
e[0][pos1(i+1,j)]=e[2][pos1(i,j)]=s[j]-'0';
}
for(int i=1;i<=q;++i){
scanf("%d %d %d %d",&a[i].col,&a[i].lv,&a[i].x,&a[i].y);
a[i].id=i;
}
std::sort(a+1,a+q+1,cmp_lv);
for(int i=1;i<=q;++i)
a[i].lv=i;
std::sort(a+1,a+q+1,cmp_id);
for(int i=1;i<=q;++i)
val[pos1(a[i].x,a[i].y)]=i;
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
//先将同一连通块上的并查集维护,再维护线段树信息,可以省去合并线段树的复杂度
int id=pos1(i,j);
for(int k=0;k<4;++k){
if(e[k][id]>1){
int nxt=pos1(i+dx[k],j+dy[k]);
if(val[id]==0 && val[nxt]==0){
dsu[(e[k][id]==3)?0:(k%2+1)].merge(id,nxt);
}
}
}
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
//维护线段树信息,包括自己所在的行列和可以到达的棋子的等级
int id=pos1(i,j);
int idfa=dsu[0].getfa(id);
st[2].root[idfa]=st[2].ins(st[2].root[idfa],1,n*m,pos2(i,j));
st[3].root[idfa]=st[3].ins(st[3].root[idfa],1,n*m,id);
for(int k=0;k<4;++k){
if(e[k][id]==3){
int nxt=pos1(i+dx[k],j+dy[k]);
if(val[nxt]){
int col=a[val[nxt]].col;
st[col].root[idfa]=st[col].ins(st[col].root[idfa],1,q,a[val[nxt]].lv);
}
}
}
}
}
for(int i=q;i>=1;--i){
int id=pos1(a[i].x,a[i].y);
int col=a[i].col;
for(int j=0;j<4;++j){
//处理边权为3的线段树,把棋子自身删除
if(e[j][id]==3){
int nxt=pos1(a[i].x+dx[j],a[i].y+dy[j]);
int nxtfa=dsu[0].getfa(nxt);
st[col].root[nxtfa]=st[col].ins(st[col].root[nxtfa],1,q,a[i].lv,-1);
}
}
for(int j=0;j<4;++j){
//合并边权为3的所有并查集,同时合并线段树
if(e[j][id]==3){
int nxt=pos1(a[i].x+dx[j],a[i].y+dy[j]);
if(val[nxt] && val[nxt]<i)
continue;
//若出现还没有被删除的棋子,直接跳过
dsu[0].merge(id,nxt,1);
}
}
int idfa=dsu[0].getfa(id);
//首先将并查集内的所有确定点加入ans,再将所有边界上颜色不同级别更小的棋子加入
ans[i]=dsu[0].getsize(id)+st[1^col].query1(st[1^col].root[idfa],1,q,a[i].lv);
for(int j=0;j<4;++j){
//合并边权为2的并查集
if(e[j][id]==2){
int nxt=pos1(a[i].x+dx[j],a[i].y+dy[j]);
if(val[nxt] && val[nxt]<i)
continue;
//若出现还没有被删除的棋子,直接跳过
dsu[j%2+1].merge(id,nxt);
}
}
//计算边权为2的贡献,由于编号的影响同一列上的元素并不连续,所以要除以m
int mx1=dsu[1].getmaxn(id),mx2=dsu[2].getmaxn(id),mn1=dsu[1].getminn(id),mn2=dsu[2].getminn(id);
ans[i]+=mx2-mn2+1+(mx1-mn1)/m+1;
int dmx=pos2(getxy(mx1).first,getxy(mx1).second);
int dmn=pos2(getxy(mn1).first,getxy(mn1).second);
//将2,3重复的部分删除(将2中的行/列放到3中的并查集内找)
ans[i]-=st[2].querynum(idfa,dmn,dmx)+st[3].querynum(idfa,mn2,mx2);
//特殊处理2的边界,若可以吃子且没有被3的边界包含进去就计入答案
if(e[0][mn1]==2 && caneat(i,val[mn1-m]))
if(!st[1^col].query2(st[1^col].root[idfa],1,q,a[val[mn1-m]].lv))
++ans[i];
if(e[1][mn2]==2 && caneat(i,val[mn2-1]))
if(!st[1^col].query2(st[1^col].root[idfa],1,q,a[val[mn2-1]].lv))
++ans[i];
if(e[2][mx1]==2 && caneat(i,val[mx1+m]))
if(!st[1^col].query2(st[1^col].root[idfa],1,q,a[val[mx1+m]].lv))
++ans[i];
if(e[3][mx2]==2 && caneat(i,val[mx2+1]))
if(!st[1^col].query2(st[1^col].root[idfa],1,q,a[val[mx2+1]].lv))
++ans[i];
//处理边权为1的边
for(int j=0;j<4;++j){
if(e[j][id]==1){
int nxt=pos1(a[i].x+dx[j],a[i].y+dy[j]);
//若有棋子判断是否能吃,然后都要判断是否被包含
if(val[nxt] && val[nxt]<i){
if(caneat(i,val[nxt]) && (st[1^col].query2(st[1^col].root[idfa],1,q,a[val[nxt]].lv)==0))
++ans[i];
}
else if(dsu[0].getfa(id)!=dsu[0].getfa(nxt)){
ans[i]=ans[i]+1;
}
}
}
//在计算边权为2时自己多算了1次,减掉
--ans[i];
}
for(int k=1;k<=q;++k){
printf("%d\n",ans[k]);
}
}
return 0;
}