APIO 从 CF 搬的题,模拟赛又搬了一遍/jy。
首先考虑暴力怎么做,即做 \(n\) 次树形 DP,设 \(f_{i,0}\) 表示强制删掉 \((i,fa_i)\) 这条边的最小代价,\(f_{i,1}\) 表示强制保留 \((i,fa_i)\) 这条边的最小代价。
对于一个点 \(u\),在限制度数为 \(x\) 时,对于 \(f_{i,0}\) 需要删 \(deg_u-x-1\) 个儿子,\(f_{i,1}\) 需要删 \(deg_u-x\) 个儿子。
删去 \((u,v)\) 的代价是 \(val+f_{v,0}\),不删的代价是 \(f_{v,1}\)。首先强制一条边都不删,然后我们选一些儿子用 \(cost=val+f_{v,0}-f_{v,1}\) 来替代,我们要选择最小的一些 \(cost\) 加到 \(f_u\) 里,需要排序,复杂度为 \(\mathcal O(n^2\log n)\)。
考虑如何优化,观察题目中的限制,度数是一个比较特殊的东西,手玩几组数据可以发现对于一个度数较小的节点,在 \(x>=deg_u\) 的时候,\(f_{u,0}\) 和 \(f_{u,1}\) 都选择了全部的儿子,没有进行替代操作,但对于每次 DP 它都需要计算一次,非常的呆,考虑删去这些节点,把这个节点的东西存在它相邻的有用的节点即度数 \(>x\) 的节点里。然后每次只 DP 度数 \(>x\)
的点,这样复杂度就是对的,因为 \(\sum deg=2n-2\),而一个点被 DP,当且仅当 \(x\in[0,deg]\),这样一个点最多被计算 \(deg\) 次。
记当前度数限制为 \(x\),设 \(deg_u\leq x\) 的点为无用点,\(deg_u>x\) 的点为有用点,我们对于当前的答案只需要 DP 有用点,对于已经无用的点 \(u\),它的 \(f_{u,0}\) 和 \(f_{u,1}\) 之间只差了一个 \((u,fa_u)\) 的权值(因为它不需要删任何子树内的边,只需要满足 DP 状态的限制),所以它的 \(cost\) 就是一条边权 \(val\)。
但是这样可能会出现一个点变成了无用点,它的父亲是有用点,儿子也是有用点,此时我们不需要 DP 它,但是需要 DP 它的父亲和儿子。
考虑删掉一些无用点后会形成若干个连通块,在对它的父亲所在连通块 DP 时可以把它直接看成叶子,而对于它的儿子所在连通块 DP 是可以把也它看成叶子,这样一个点可能有多个父亲,但是由于它是无用的,它的 \(cost\) 只和边权有关,删掉它的时候只考虑连接它的有用点并想办法存下它的 \(cost\) 即可。而对于无用点和无用点之间的边,我们一定会选择保留,所以这部分是不需要考虑的。
图大概是这样的:
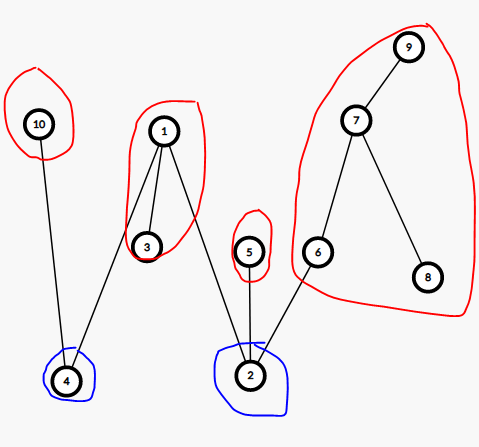
其中 \(2,4\) 是无用点,剩下的都是有用点,对于一个红色的连通块,它的内部仍然先原来一样 DP,只不过它还连了一些无用点,这些无用点对它有一个 \(cost\) 的影响,即选择 \(cost\) 来替代是是不一定全需要从它的有用点子树里找,也可以选无用点,所以我们现在的问题是如何解决无用点对有用点的贡献。
暴力计算是不对的,因为我们上面只保证了 DP 有用点点数的正确性,如果对于每个有用点都扫一遍连接它的所有无用点,那一个菊花就噶了。
但是发现 DP 连接有用点和有用点的边的总个数也是线性的,刚刚复杂度假掉的原因是计算了有用点和无用点的边所以我们考虑用一个数据结构维护一个点的所有 \(cost\),然后从中选一些最小的。
理一下思路,我们需要支持加数(无用点对于有用点以及有用点的有用点儿子对他自己的 \(cost\)),删数(当前有用点的儿子可能在 \(x\) 时的 \(cost\) 和在 \(x+1\) 时不同,所以 DP 完一次要删掉一个有用点的儿子对他自己的 \(cost\)),可以用堆维护,这样总复杂度就是 \(\mathcal O(n\log n)\)。
代码也不太好写,有注释,一不小心复杂度就假了。
struct Heap
{
priority_queue<int> q1,q2;
int sum;
inline void add(int x){q1.e(x),sum+=x;}
inline void del(int x){q2.e(x),sum-=x;}
inline void update(){while(!q1.empty()&&!q2.empty()&&q1.top()==q2.top())q1.pop(),q2.pop();}
inline int top(){return update(),q1.top();}
inline void pop(){sum-=top(),q1.pop();}
inline int size(){return q1.size()-q2.size();}
}a[250001];//可删堆
vector<pii> T[250001];
vector<int> ins,ers,ans;
int pos,dg,vis[250001],f[250001][2],n,deg[250001],p[250001];
bool cmp(pii x,pii y){return deg[x.fi]>deg[y.fi];}
bool cmp2(int x,int y){return deg[x]<deg[y];}
inline void del(int k){for(auto [to,v]:T[k])if(deg[to]<=dg)break;else a[to].add(v);}//删除无用点是把它的 $cost$ 即边权 $v$ 存到它旁边的所有有用点的堆里
inline void dfs(int k,int fa)
{
int del=deg[k]-(vis[k]=dg);//需要删的边数
while(a[k].size()>del)a[k].pop();//删的边一定越来越少,堆里存太多无用点也是没用的,只保留cost最小的
for(auto [to,v]:T[k])if(to!=fa){if(deg[to]<=dg)break;else dfs(to,k);}//按度数排序后只DP有用点
ins.clear(),ers.clear();
//ins 存的有用点儿子的所有 cost,在最后把它删掉
//在找前 del 大的时候需要弹堆知道 siz=del,可能会弹出一些需要保留的无用点的 cost
//ers 存的不小心被弹出的无用点的 cost,它还是有用的
int sum=0;
for(auto [to,v]:T[k])
{
if(to==fa)continue;
if(deg[to]<=dg)break;
int val=f[to][0]+v-f[to][1];sum+=f[to][1];//val 即 cost
if(val<=0)ans[dg]+=val,--del;
//有时删边比留边优秀,而对于删边是没有限制的,可以把它连接的边全删了即把 del 减成负数,要加特判,否则 WA on test 4
else a[k].add(val),ins.eb(val);
}
while(a[k].size()&&a[k].size()>del)ers.eb(a[k].top()),a[k].pop();//删 deg-x 条
f[k][1]=sum+a[k].sum;
while(a[k].size()&&a[k].size()>=del)ers.eb(a[k].top()),a[k].pop();//删 deg-x-1 条
f[k][0]=sum+a[k].sum;
for(int x:ers)a[k].add(x);
for(int x:ins)a[k].del(x);
}
vector<int> minimum_closure_costs(signed N,vector<signed> U,vector<signed> V,vector<signed> W)
{
n=N,ans.resize(n);int x,y,z;
for(int i=1;i<n;++i)x=U[i-1]+1,y=V[i-1]+1,z=W[i-1],ans[0]+=z,++deg[x],++deg[y],T[x].eb(mp(y,z)),T[y].eb(mp(x,z));
for(int i=1;i<=n;++i)sort(T[i].begin(),T[i].end(),cmp),p[i]=i;//把边按 deg 排序保证复杂度
sort(p+1,p+1+n,cmp2);//把点按 deg 排序保证复杂度
for(dg=1,pos=1;dg<n;++dg)
{
while(pos<=n&°[p[pos]]<=dg)del(p[pos++]);//p_pos 变成无用点
if(pos>n)break;
for(int j=pos;j<=n;++j)if(vis[p[j]]!=dg)dfs(p[j],0),ans[dg]+=f[p[j]][1];
}
return ans;
}