介绍
1979年Shamir在下文提出基于拉格朗日插值多项式的\((r,n)\)秘密共享方案(\(0<r \leq n\))。秘密拥有者通过构建一元多项式将秘密分为\(n\)份,接收方收集大于等于\(r\)份的子秘密即可重构多项式恢复秘密。

方案
\((r,n)\)秘密共享方案分为秘密分享和秘密重构两步:
- 秘密分享
假设有一个秘密\(M\),取\(r-1\)个随机数\(d_1,d_2,...,d_{r-1}\),构造一个\(r-1\)次一元多项式\(w(x)=M+d_1x+d_2x^2+...+d_{r-1}x^{r-1}\)。
\(x\)取\((1,...,n)\),计算出\(n\)个子秘密\((x,w(x))\),将这\(n\)个子秘密发送给\(n\)个不同的人。
- 秘密重构
当有不少于\(r\)个不同的子秘密聚在一起时,根据拉格朗日插值,可以唯一插值出一个\(r-1\)次多项式,即:
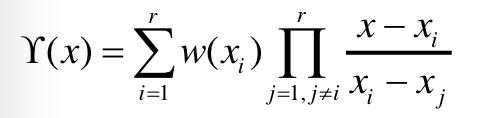
也可以看作是:\(w(x)=M+d_1x+d_2x^2+...+d_{r-1}x^{r-1}\),另\(x=0\),就可以得到秘密\(M=w(0)\)。
实验
import random
from decimal import Decimal
FIELD_SIZE = 10**5 # GF域大小
def reconstruct_secret(shares):
"""
Combines individual shares (points on graph)
using Lagranges interpolation.
`shares` is a list of points (x, y) belonging to a
polynomial with a constant of our key.
"""
sums = 0
for j, share_j in enumerate(shares):
xj, yj = share_j
prod = Decimal(1)
for i, share_i in enumerate(shares):
xi, _ = share_i
if i != j:
prod *= Decimal(Decimal(xi)/(xi-xj))
prod *= yj
sums += Decimal(prod)
return int(round(Decimal(sums), 0))
def polynom(x, coefficients):
"""
This generates a single point on the graph of given polynomial
in `x`. The polynomial is given by the list of `coefficients`.
"""
point = 0
# Loop through reversed list, so that indices from enumerate match the
# actual coefficient indices
for coefficient_index, coefficient_value in enumerate(coefficients[::-1]):
point += x ** coefficient_index * coefficient_value
return point
def coeff(t, secret):
"""
Randomly generate a list of coefficients for a polynomial with
degree of `t` - 1, whose constant is `secret`.
For example with a 3rd degree coefficient like this:
3x^3 + 4x^2 + 18x + 554
554 is the secret, and the polynomial degree + 1 is
how many points are needed to recover this secret.
(in this case it's 4 points).
"""
coeff = [random.randrange(0, FIELD_SIZE) for _ in range(t - 1)]
coeff.append(secret)
return coeff
def generate_shares(n, m, secret):
"""
Split given `secret` into `n` shares with minimum threshold
of `m` shares to recover this `secret`, using SSS algorithm.
"""
coefficients = coeff(m, secret)
shares = []
for i in range(1, n+1):
x = random.randrange(1, FIELD_SIZE)
shares.append((x, polynom(x, coefficients)))
return shares
# Driver code
if __name__ == '__main__':
# (3,5) sharing scheme
t, n = 3, 5
secret = 1234
print(f'Original Secret: {secret}')
# Phase I: Generation of shares
shares = generate_shares(n, t, secret)
print(f'Shares: {", ".join(str(share) for share in shares)}')
# Phase II: Secret Reconstruction
# Picking t shares randomly for
# reconstruction
pool = random.sample(shares, t)
print(f'Combining shares: {", ".join(str(share) for share in pool)}')
print(f'Reconstructed secret: {reconstruct_secret(pool)}')
## 输出
Original Secret: 1234
Shares: (85479, 169064248999330), (64655, 96725154480594), (47701, 52649409201294), (99941, 231110282437614), (93923, 204115595277642)
Combining shares: (47701, 52649409201294), (64655, 96725154480594), (99941, 231110282437614)
Reconstructed secret: 1234
总结
秘密共享方案广泛应用于要求信任是分布式而不是集中式的密码系统中。使用秘密共享的真实场景的突出例子包括:
- 基于阈值的比特币签名
- 安全多方计算
- 具有多方计算的私有机器学习
- 密码管理