首页 > 其他分享 >3、进制数转换

3、进制数转换

时间：2023-10-08 17:47:49浏览次数：32  
标签：十六进制 转换 进制 转换成 二进制 八进制 十进制

1、计算机信息的表示（存储）

1.1、例题解析

往年考过一道大题，问：数据和信息的关系是什么？

如果这么答，拿不到全分（数据是信息的载体，而信息是数据的解释），这样是不行的

我们需要单独解释下数据和信息是什么，再说他们的关系

  • 数据是反映客观事物属性的记录，是信息的具体表现形式，数据进过加工处理后，就成为了信息；
  • 而信息需要经过数字转化变成数据才能进行存储和传输
  • 数据信息分为数值型（0,1,2,3,）和非数值型（a-z，A-Z,中文，视频，文档）
  • 计算机能够区分不同的信息（计算机都是二进制），是因为他们采用了不同的编码规则(识别不同的，那么就是采用不同的二进制编码规则)

1.2、数制

也被称作===计数制，是指用一组 “固定的符号” ，和 “统一的规则” 来计数的方式

  • 十进制（十进位计数制），生活中常用
  • 二进制：计算机当中使用
  • 除此：还有八进制（linux的权限），十六进制（一般用于内存编制，编号）

1.3、四个概念

  1. 数码
    • 在数制这个规则下，表示基本数值的大小的不同数字符号
    • 简单点讲就是，每个进制表示的数字不同，并且每个进制能使用的数字也不同
  2. 基数
    • 数制当中能使用数码的个数，（他是几进制，就能使用几个数码）
  3. 位权
    • 数制当中每个位置的价值
  4. 标识
    • 为了区分不同的进制,在数字后面加上相应的字符或者括号外加上数字下标
    • 例如下面这个
    • image-20220725122812225

1.4.各个进制的概念图解

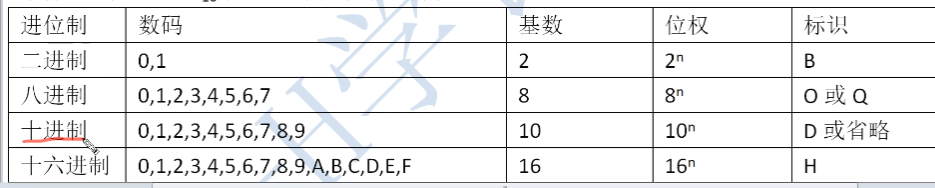
image-20220725122855745

image-20220725123243727

  • 我们这里可以看到 十六进制的数码表示的有点不一样
  • 原因是：如果十六进制代表的是0-15，那么在使用10-15的时候，会出现所谓的歧义
  • 也就是多位数码之间，没有办法区分
  • 例如
  • 1115 === 它可以代表 1 1 1 5，也可以代表 11 15 || 1 11 5
  • 这样就会发生歧义，导致我们无法对数据进行解密，转码等操作

1.5、问题引出 == 标识的作用

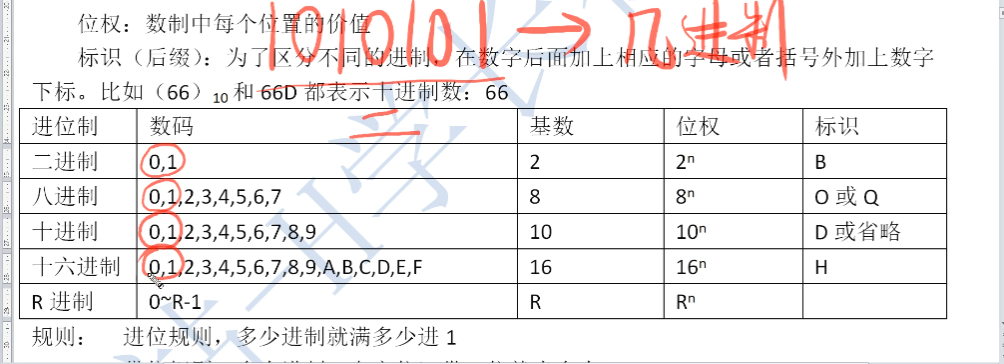
image-20220725123808329

  • 问了这么一个问题，10101是几进制？

  • 在思维定式下，下意识回答二进制，但实际上0和1都是可以出现在其他进制当中的

  • 这也是一种歧义的存在方式之一，那么面对这种歧义的情况，我们应该如何解决？

  • 这个时候我们就需要使用我们之前提过的标识了

  • 讲标识的时候需要注意以下几点

    1. 标识可以有两种写法，一种是括号下标，另一种是在数字后面加上相应的标识字母
    2. 十进制一般是不写标识的
    3. 二、八、十六进制的标识符需要背一下，括号下标的方式肯定要简单点

  • 看下面几个例子

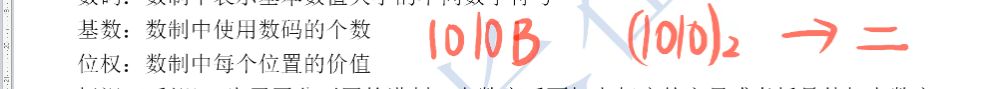
    • image-20220725124259796
    • 他们都代表二进制，从写法上来看，我个人认为括号下标的观赏性要更强一点
    • 因为16进制也是存在字母B的

1.6、固定规则

1、进位规则

image-20220725131931733

  • 俗话说得好，进位规则，多少进制满多少，那么就向前进一
  • 可以看上面的图，用十进制举例，9+1按照我们通俗的思想他就等于10
    • 9在十进制当中属于价值最大的数，他 + 1 满10，那么就向前进一位
  • 我感觉我的解释还是有点片面，等后面熟悉了在说

2、借位规则

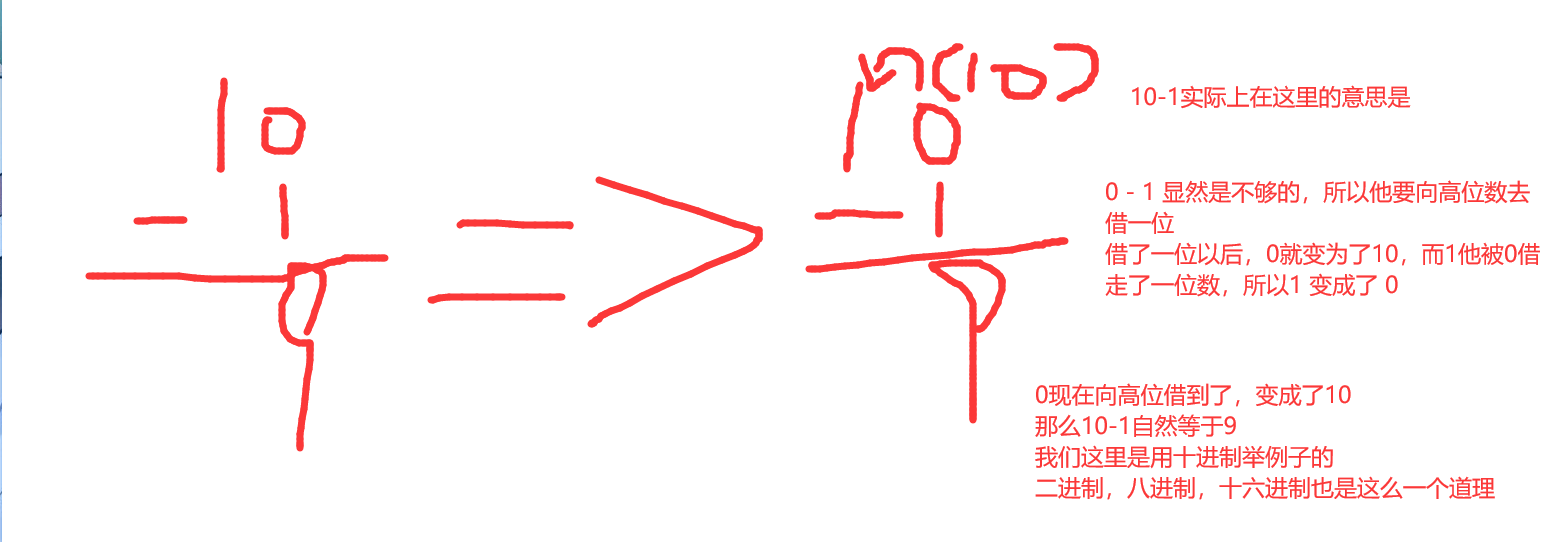
image-20220725132834425

  • 上述就是我的解释，放在二进制，八进制，十六进制当中也是一个道理
  • 忘了的话用计算机来计算就可以了

image-20220725133346589

十六进制单独讲一个例子，巩固记忆

11 - 2 为什么等于F？

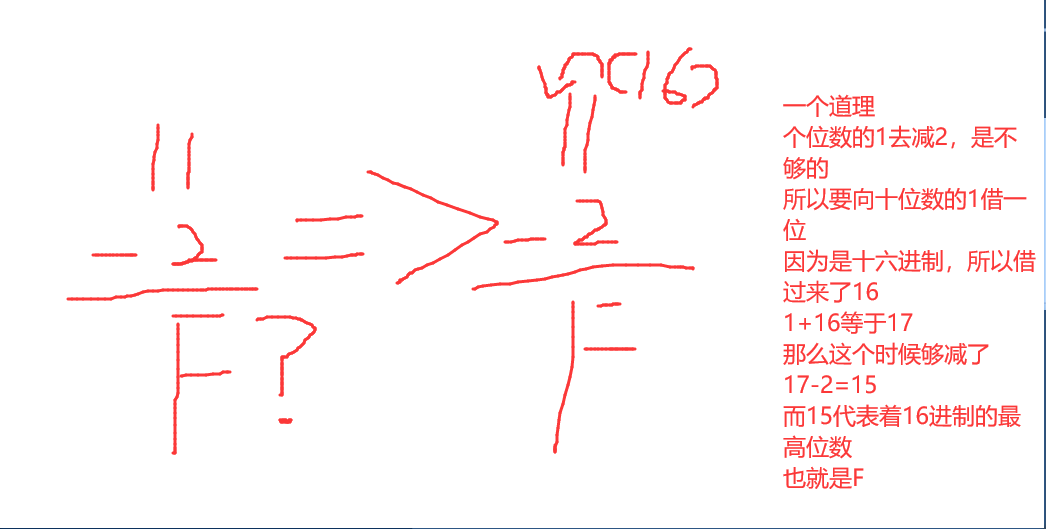
image-20220725133629508

image-20220725133851545

最后一个十六进制的写法，为什么H会多加一个空格，应该是为了怕混淆视听，本身ABCDF是没错的

2、进制转换

2.1、十进制 => R进制

  • 这里的R指的是，十进制转换成任意进制
  • 这里提到了一个东西叫做 十进制转换成R进制,实际上这个R进制就是代表你即将要转换的一个进制
  • 我们这里记住一个口诀
    1. 整数部分：除以R，反向取余
    2. 小数部分：乘以R，正向取整
  • 我们这里看几个例子，我自己手写几个例子

img

image-20220725141140754

2.2、R进制转换成十进制

  • 有了之前的了解，现在我们将任意进制转换成十进制相信理解上应该会简单一点
  • 关于R进制转换成十进制，这里有一套口诀
    • 乘权求合法： 每一位 的值，乘以对应的价值(位权)
    • 标位权的时候注意以下两点
      1. 从个位开始标，小数和整数分开
      2. 位权是 0指数 开始,也就是（XXX的0次方开始）

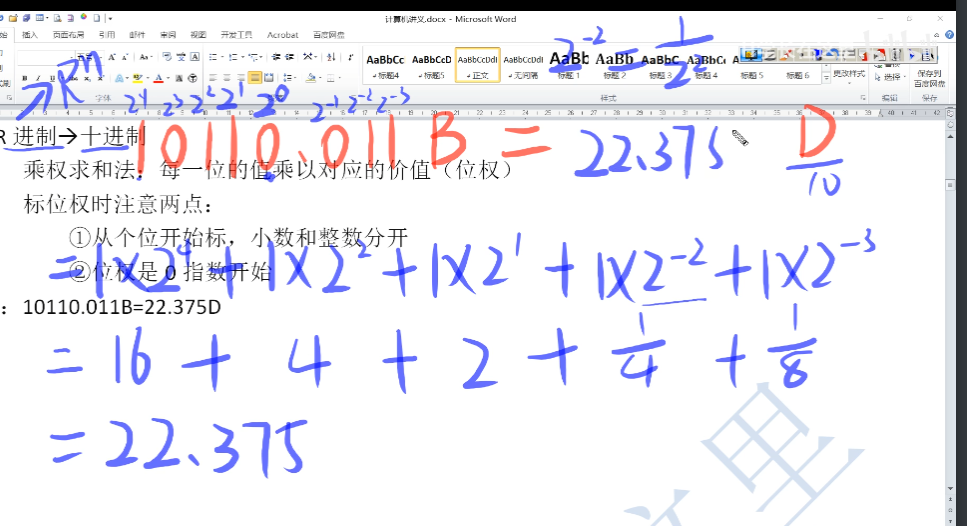
1、例题

10110.011B => ?D

运算过程

image-20220725151934585

2、八进制转换十进制

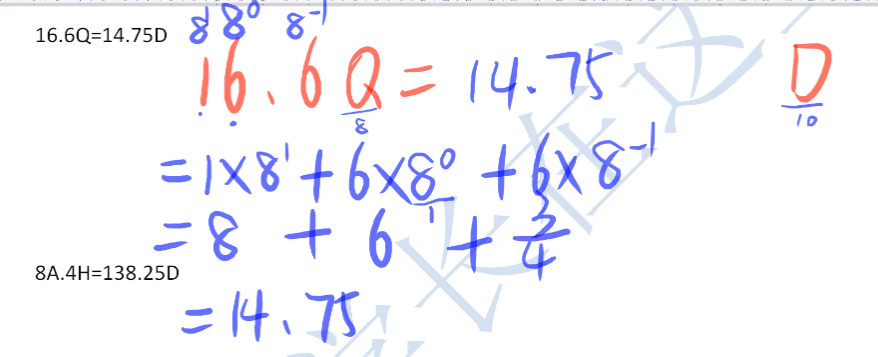
image-20220725152452402

3、十六进制转换十进制

8A.4H = ? D?

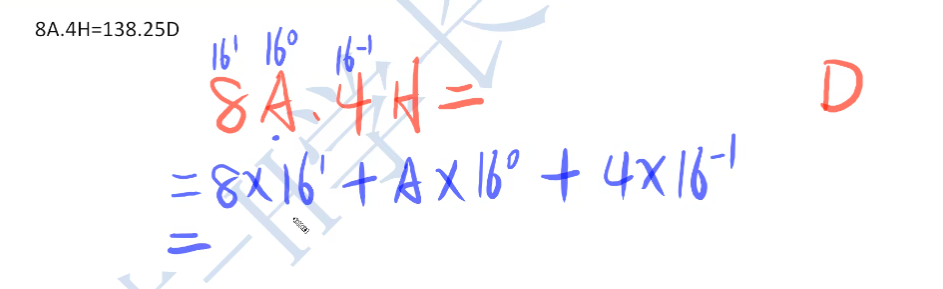
image-20220725152753873

重点

  • 虽然A代表的是10，但是8A不能写作810
  • 虽然A是10，但是它的位权只有一位
  • 所以应该向上面那样写

2.3、8421拼凑法（二进制<=>十进制）

下面这部分其实就相当于乘权法，背出基本的2-10的次方

image-20220725153306731

  • 十进制和二进制相互转换一个比较简单的算法
  • 我们来看个例子

1、十进制转二进制

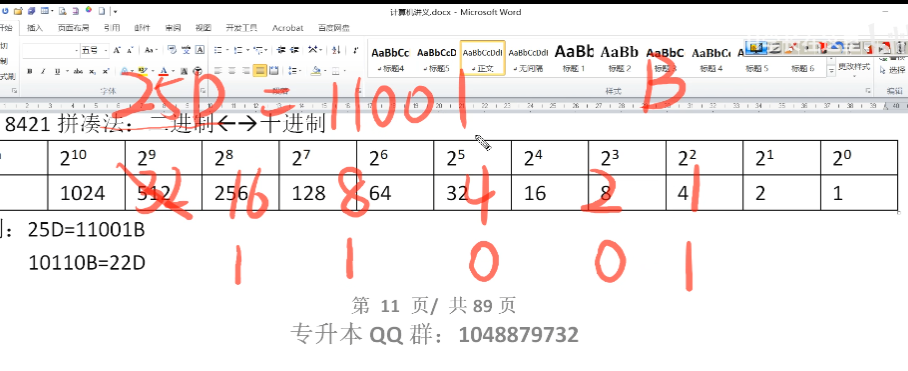
image-20220725153946752

解析

  1. 十进制数25，那么我们依次将2的n放列举出来，找出最接近这个十进制数的二进制数
  2. 例如这里最接近25，并且比25小的二进制数为16
  3. 那么按照上面的方式我们将16 => 后面的数依次组合就形成了我们的二进制数
  4. 组成25需要：1个16、1个8、0个4 、 0个2 、1个1
  5. 所以快速得出25D = 11001B

2、二进制转换十进制

  • 其实做法和之前一样，也是例举出来，但是这个时候我们记下来的2的n方就很有用了，信手拈来

image-202207251543410853、我自己出个题

我自己出题喜欢出稍微难度大点的，问：2578D转换为二进制是多少？

image-20220725154751414

  • 还是一样，依次例举出来，最接近2578，并且比2578小的数就是2048
  • 那么就把2048往后的数依次写出来就行了
  • 最终计算结果为 1010 0000 1001 0
  • 计算器验证一下我们算的对否
  • 计算机验证结果
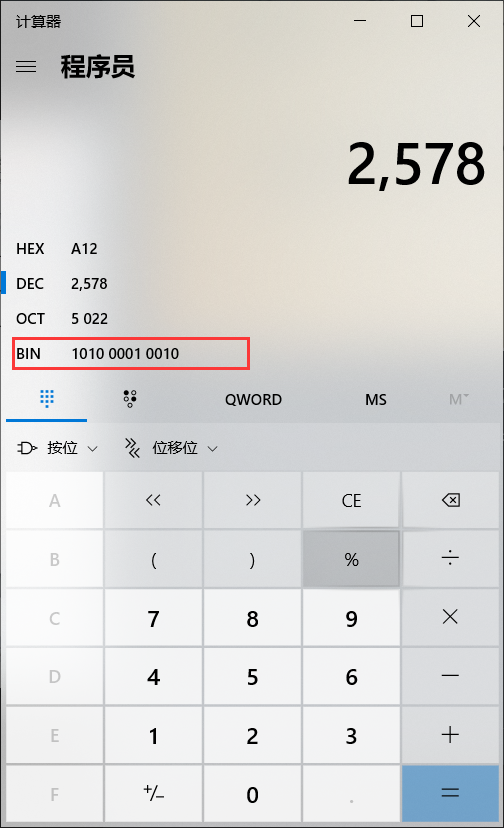
  • image-20220725154947325
  • emmm，是我哪里写错的了，我看错了
  • image-20220725155032937

2.4、二进制->八进制->十六进制

1、分组转换法

  • 二转八：3位转换成1位
  • 二转十六：4位转换成一位
  • 注意
    1. 以小数点为界，整数和小数分开
    2. 整数位数不够在前面添0，小数位数不够在后面添0

2、例题

image-20220725162059230

10101.1B = ？Q？

image-20220725163452915

110101.1101B = ?H?

image-20220725164346190

2.5、八进制，十六进制转换成二进制

1、还组转换法

  • 八进制转换二进制： 1位还为3位
  • 十六进制转换成二进制：1位还为4位

2、例题

16.32Q = ？B？（八转二）

image-20220725165225694

F.3DH => ？B

注意，F和D只能占1位，不能拆开，我第一次计算的时候就犯了这个错

image-20220725165953584

2.6、八进制转换成十六进制

  • 要点
  • 以二进制为 “桥梁”
  • 实际操作结果就是
    1. 八进制先转换成二进制
    2. 二进制在转换成十六进制

image-20220725170326092

标签：十六进制,转换,进制,转换成,二进制,八进制,十进制
From： https://www.cnblogs.com/wavesbright/p/17749709.html

相关文章

  • C#学习笔记--变量类型的转换
    变量类型的转化：转换原则同类型的大的可以装小的，小类型的装大的就需要强制转换。隐式转换：同种类型的转换：//有符号long——>int——>short——>sbytelongl=1;inti=1;shorts=1;sbytesb=1;//隐式转换int隐式转换成了long//可以用大范围装小范围的类型（隐......
  • 二进制码部分知识回顾
    &：与相同1为1，不同为0000000101111111100000000 |：或相同0的为0，不同为1000000101111100111111011 ~：非0变1,1变00000001011111101 <<：左移相当于乘以2inta=1;==>00000001a<<1;a==>左移1位==>00000010【左移可以循环，由编译器决定】：比如a=1左......
  • Python入门示例系列12 数据类型转换
    Python入门示例系列12数据类型转换 type()函数使用type()函数可以查看数据类型。示例：>>>type(123)<class'int'>>>>type(12.3)<class'float'>>>>type("abc")<class'str'>>>>type([1,2,3])......
  • Qt中文编码的转换
    Windows容易出现GBK编码乱码的问题，这里使用QTextCodec来转码：假设你现在的编码是utf8，但是显示在windows上是乱码，那么你可以尝试以下操作：//utf8转GBKQStringbuf="你好";QTextCodec*code=QTextCodec::codecForName("gb2312");QByteArrayarr=code->fromUn......
  • 类型转换
    类型转换由于Java是强类型语言,在进行某些计算时,需要用到类型转换低--------------------------------高byte,short,char<int<long<float<double 运算中,不同类型的数据需转化为同一类型,再进行运算强制类型转换(低-->高)自动类型转换(高-->低)......
  • BL124CN：高效稳定地实现CANOPEN和Ethernet/IP协议间的无缝转换
    BL124CN是一款功能强大的转换器，它能够将CANOPEN、JAE1939和DeviceNet等协议转换为Ethernet/IP上行协议，为用户提供了更加便捷和灵活的网络连接方式。针对下行协议（CANOPEN、JAE1939和DeviceNet），BL124CN能够实现实时的数据转换和传输。CANOPEN是一种用于控制和通讯领域的通信协议，广......
  • ansible-playbook实现MySQL的二进制部署
     #安装mysql5.6[root@ansible~]#ls-l/data/ansible/files/mysql-5.6.46-linux-glibc2.12-x86_64.tar.gz-rw-r--r--1rootroot403177622Dec 413:05/data/ansible/files/mysql-5.6.46-linux-glibc2.12-x86_64.tar.gz[root@ansible~]#cat/data/ansible......
  • TCP Socket 数据发送和接收时进制转换
       确实经过了转换：十六进制--》十进制--》ASCII字符十六进制的61，对应十进制的97，对应ASCII字符a https://blog.csdn.net/cybersnow/article/details/88079026C#代码：//16进制字符串转字节数组  格式为stringsendMessage="000100000006FF0500640......
  • SpringMVC 类型转换
    SpringMVC类型转换Spring引入通用的数据类型转换系统，其定义了SPI接口和相应的运行时执行类型转换的API，提供无状态、强类型其可以在任意类型之间进行类型转换，可以用于任何需要的地方(如SpEL、数据绑定等)内置类型转换器<!--开启类型转换服务--><mvc:annotation-drivenconver......
  • 位运算分为位逻辑运算与移位运算(对应二进制位)
    位运算分为位逻辑运算与移位运算(对应二进制位)： 注：在逻辑运算中，数学表示符于编程逻辑的对应关系为：∧表示与∨表示或¬表示非含义C++语言表示规则与运算a&b都为1时为1，反之为0。或运算a|b两个数其中一个为1就为1，反之为0。异或运算a^b两个数不同时结果为1，......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99