Description
从前有一只小皮卡丘,这只小皮卡丘非常聪明,他喜欢和大皮卡丘玩这样一个猜数游戏——给定 \(n\) 个数,要猜的数字在 \(1\sim n\) 之间,猜一个数 \(i\) 会花费 \(a_i\) 的代价。每次大皮卡丘猜完一个数,小皮卡丘会告诉他大了还是小了。大皮卡丘想问你在最坏情况下他至少要花多少代价?
\(n\le 7000\)。
Solution
我们会发现这个每次猜一下其实就可以缩小我们答案的区间。这道题是个最优化问题,我们肯定首选 dp。\(n\le 7000\) 看上去很可以 \(f(l, r)\) 代表答案在 \([l, r]\) 内的最坏情况下要花的最小代价。
然后转移就很简单,每次猜一个答案 \(k\)。由于小皮卡丘很坏,所以它肯定会把大皮卡丘往大的方向引导,所以 \(f(l, r) = \min\{\max(f(l, k), f(k + 1), r) +a_k\}\)。但是我们会发现这是 \(O(n^3)\) 的我过不了。怎么办?
观察这个 dp 式子,这个里面有一个 \(\max\{f(l, k), f(k + 1, r)\}\)。我们看它很不顺眼,因为有个 \(max\) 我就根本没办法用任何方法优化。怎么办?拆掉。怎么拆?
我们观察一下,让 \((l, r)\) 作为状态看成定值,那么随着 \(k\) 增大,我的 \(f(l, k)\) 也会增大,\(f(k + 1, r)\) 会减小。此时我们就可以考虑先求出什么情况下哪个大,然后我们挨个优化。我们可以画一张简单的示意图
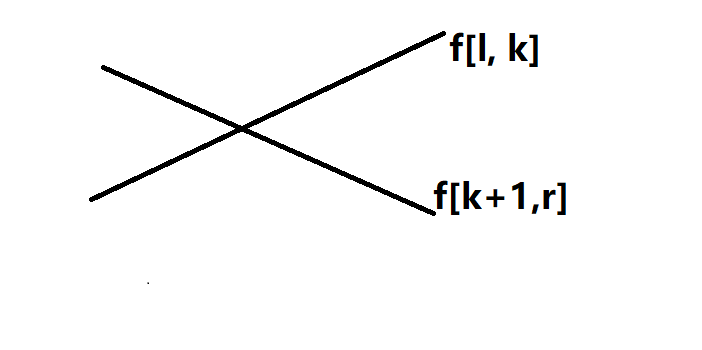
发现了没有?中间有一个交点,这个交点我们记为 \(X\),具体来说 \(X\) 代表最大的满足 \(f(l, X) < f(X + 1, r)\) 的位置。如果我们拥有了这个 \(X\),我们就可以知道 \(f(l, k)\) 和 \(f(k + 1, r)\) 谁大谁小了!
然后我们对 \(k\) 进行分讨——
-
\(k\le X\),此时 \(f(l, k) < f(k + 1, r)\),那么 \(f(l, r) = \min_{l\le k \le X}\{f(k + 1, r)\ + a_k\}\)。聪明的你看到这个 dp 式子,你想到了什么?单调队列!但是这个东西吧你就不能无脑的单调队列,为啥咧?比如我们按照一般的 dp 顺序,枚举一个 \(len\),然后升序枚举 \(l\) 再枚举 \(r\),这个时候我的 \(r\) 也是变量,这是不行的,我们得让 \(r\) 变成一个定值。
聪明的你就会想到,我们从小到大在外层枚举 \(r\),在内层从大到小枚举 \(l\)(为什么从大到小?这是因为这样满足区间长度逐渐变大,区间长度是区间 dp 的阶段),然后我就可以成功的把 \(r\) 看成常量了,我就可以成功的单调队列了。 -
\(k > X\),此时 \(f(l, k)\ge f(k + 1, r)\)。因为 \(a_i\) 递增,所以我 \(f(l, k) + a_k\) 也递增,聪明的你就可以想到 \(f(l, X + 1) + a_{X+1}\) 就是最小的。