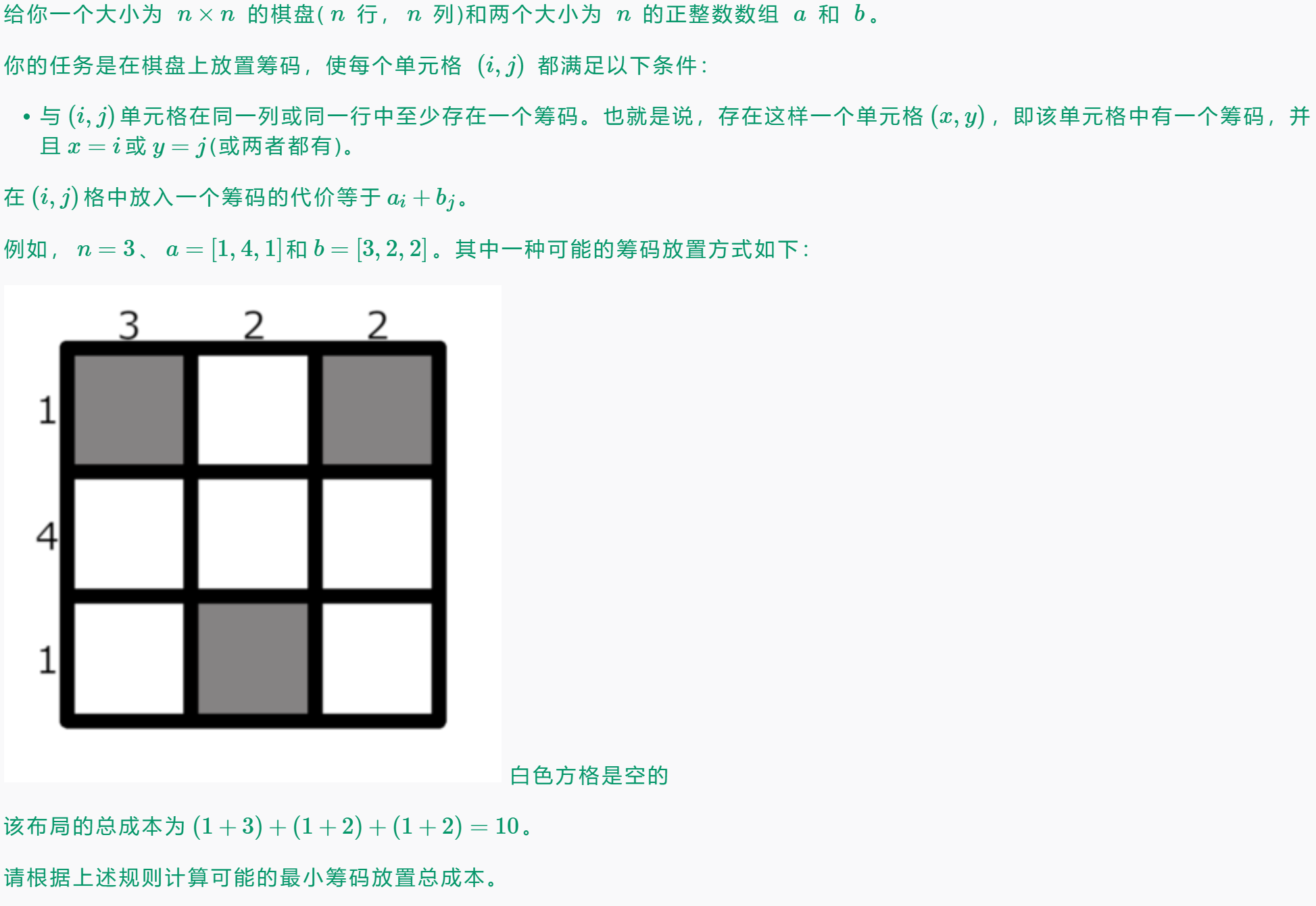
B. Chips on the Board
题解:贪心
显然我们可以把题意转化为:对于任意一个\((i,j)\),我们可以花费\(a_{i,j}\)的代价占据第\(i\)行和第\(j\)列,求占据所有格子的最小代价
考虑两种情况:
- 在每一行选一个格子
- 在每一列选一个格子
贪心选即可
int n, a[N], b[N];
void solve()
{
cin >> n;
int posa = -1, posb = -1;
for (int i = 1; i <= n; ++i)
{
cin >> a[i];
if (posa == -1 || a[i] < a[posa])
posa = i;
}
for (int i = 1; i <= n; ++i)
{
cin >> b[i];
if (posb == -1 || b[i] < b[posb])
posb = i;
}
int ans = INF, sum = 0;
for (int i = 1; i <= n; ++i)
sum += a[i];
sum += n * b[posb];
ans = min(ans, sum);
sum = 0;
for (int i = 1; i <= n; ++i)
sum += b[i];
sum += n * a[posa];
ans = min(ans, sum);
cout << ans << endl;
}
C. Make it Alternating
题解:组合数学
显然可以将字符串\(s\)分成由连续\(1\)或\(0\)组成的几段区间,那么最小操作次数显然是区间的数量
我们考虑方案数:
对于每段区间,我们必须留下一个数,假设某段区间的长度为\(len\),那么对答案的贡献为:\(ans:=ans\times len\)
那么其他没有被留下的数就要全部被删除,那么删除的顺序任意,假设被删除的数的数量为\(cnt\),那么对答案的贡献为\(ans:=ans \times cnt!\)
int n, fac[N];
void init()
{
fac[0] = 1ll;
for (int i = 1; i < N; ++i)
fac[i] = (fac[i - 1] * i) % mod;
}
void solve()
{
string s;
cin >> s;
n = s.length();
s = " " + s;
int ans1 = 0, ans2 = 1;
for (int i = 1; i < n; ++i)
ans1 += (s[i] == s[i + 1]);
int l, r, f = 0;
for (int i = 1; i < n; ++i)
{
if (!f && s[i] == s[i + 1])
{
f = 1;
l = i;
}
else if (f && s[i] != s[i + 1])
{
f = 0;
r = i;
ans2 *= (r - l + 1);
ans2 %= mod;
}
else if (f && i + 1 == n)
{
f = 0;
r = n;
ans2 *= (r - l + 1);
ans2 %= mod;
}
}
if (f)
ans2 = ans2 * (n - l + 1) % mod;
ans2 = ans2 * fac[ans1] % mod;
cout << ans1 << " " << ans2 << endl;
}
D. Sum of XOR Functions
题解:按位计算贡献
\[2^i \sum_{r = 1}^n \sum_{l=1}^r g(l,r)(r - l + 1) \]
- 我们发现,对于二进制中某一位\(i\)来说,我们考虑其对答案的贡献 :
\(g(l,r)\)为第\(i\)位二进制在\([l,r]\)中\(1\)的个数,如果\(1\)为奇数,则\(g(l,r)=1\),否则\(g(l,r) = 0\)
那么题目就转化为:对于一个\(01\)序列,固定右端点\(r\),求有多少个左端点\(l\)使得\(g(l,r)=1\)
我们定义\(pre[i]\)为\([1,i]\)的前缀异或和,那么\(pre[r] \oplus pre[l-1] = 1\)就代表\(g(l,r)=1\)
那么我们完全可以对前缀维护一个\(cnt\)和\(sum\)
所以复杂度为 \(O(30n)\)
int n, a[N];
ll add(ll a, ll b) { return (a + b) % mod; }
ll sub(ll a, ll b) { return ((a - b) % mod + mod) % mod; }
void solve()
{
cin >> n;
for (int i = 1; i <= n; ++i)
cin >> a[i];
int ans = 0ll;
// 考虑每一位二进制对答案产生的贡献
for (int i = 0; i <= 30; ++i)
{
vector<int> vec(n + 10), pre(n + 10), cnt(2), sum(2);
int res = 0ll;
cnt[0]++; // pre[0] = 0
for (int j = 1; j <= n; ++j)
{
vec[j] = (a[j] >> i & 1);
pre[j] = (pre[j - 1] ^ vec[j]);
cnt[pre[j]]++;
sum[pre[j]] += j;
res = add(res, sub((cnt[pre[j] ^ 1] * (j) % mod), sum[pre[j] ^ 1]));
}
ans = add(ans, (1ll << i) * res % mod);
}
cout << ans << endl;
}