是思路非常值得学习的一道题
第一问:
首先我们感性上觉得这题应该和LIS有一点关系,但里面有一点问题:
17 50 50 50 18
如果我们求LIS的话,我们会认为只需要改掉50 50 50即可,但其实我们只改掉这些数,我们是无法做到让数单增的
我们发现这个限制写成数学语言即为:\(a_i - a_j \geq i - j\),移项得\(a_i - i \geq a_j - j\),因此我们令\(b_i = a_i - i\),只需求出\(b_i\)的最长不降子序列,拿\(n\)减掉即可
第二问:
这个数据随机我们很难办(我当时以为会用到随机排列的LIS期望长度是\(O(\sqrt{n})\)的限制想了半天,结果发现并不是这样),因此我们考虑暴力\(dp\)
首先容易想到对于我们所求的最长不降子序列里的两个数\(b_i, b_j\),我们可以确定在\([i,j]\)的所有数值域都不可能在\([b_i,b_j]\)之间(废话)
因此我们假设存在一个策略,其中黑线表示我们在操作完后序列的样子,红点表示操作前序列的样子,红色箭头表示变化值的大小(图来自题解)
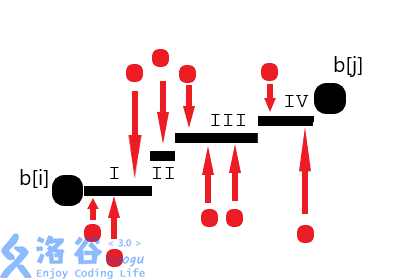
我们发现对于一条黑线,如果在他上面的点比在他下面的点多,我们把他往上移到在他右边线处更优(如II移到III处更优);如果在他下面的点比在它上面的多同理;如果双方点相同,随便移动无影响。
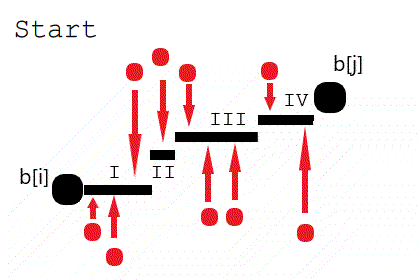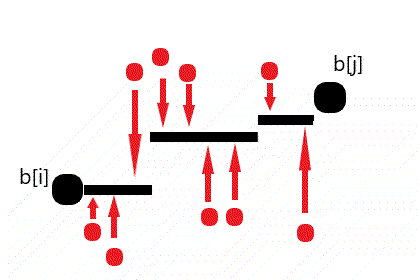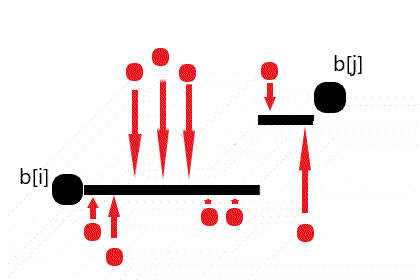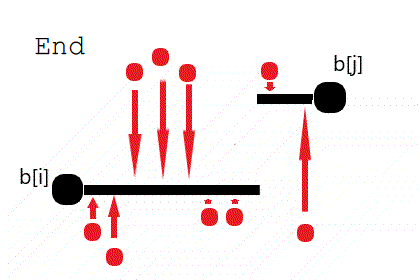
因此我们在进行若干次操作后,得到的黑线一定是被分成了两部分:\([i,k]\)的值为\(b_i\),\([k+1,j]\)的值为\(b_j\),可以证明这么做一定是不劣的
因此我们考虑一个\(O(n^3)\)的暴力\(dp\):设\(g_i\)表示以\(i\)结尾的LIS的所有可能方案的最少操作次数。设\(S\)表示\(f_i\)的所有转移前驱构成集合。我们可以得到转移方程:
\[g_i = \min_{frm \in S}{( \min_{k=frm-1}^{i}{g_{frm}+\sum_{l=frm}^{k}{|a_l-a_{frm}|} + \sum_{l=k + 1}^{i}{|a_l-a_{i}|} } )} \]因为数据随机,每个数被更新的前缀并不多,直接暴力转移即可
最终复杂度\(O(n^3)\)
u1s1,要是这题把随机性质去掉,数据范围开正常一点的话,是一个好题
标签:50,frm,P2501,HAOI2006,随机,LIS,序列,我们 From: https://www.cnblogs.com/fox-konata/p/17704539.html