差分与二维差分

标签：前缀 公式 fsum 差分 二维 数组

一、基础差分

1.问题：多次区间修改，一次单点查询
2.思路：对于区间问题，我们可以使用前缀和与线段树。线段树过于复杂，我们可以从前缀和来思考。考虑到每一次单点修改，前缀和都是又该点开始到结尾的区间修改，我们可以将原数组当做某一数组的前缀和，然后对该数组进行两次单点修改，最后再求前缀和即可。
3.由原数组推差分数组：差分是前缀和的逆运算，因而我们应该先知道前缀和公式，易得为：fsum[i]=fsum[i-1]+a[i];，对该等式进行变形，得差分公式：a[i]=fsum[i]-fsum[i-1];，而对于该公式，fsum->a,cf->差分数组.
4.结果：求前缀和即为原数组更改后
5.时间复杂度：O(m+n)

二、二维差分1

1.思路：将二维拆分为一维
2.时间复杂度:O(mn)

二、二维差分2

1.思路：同一维
2.复习二维前缀和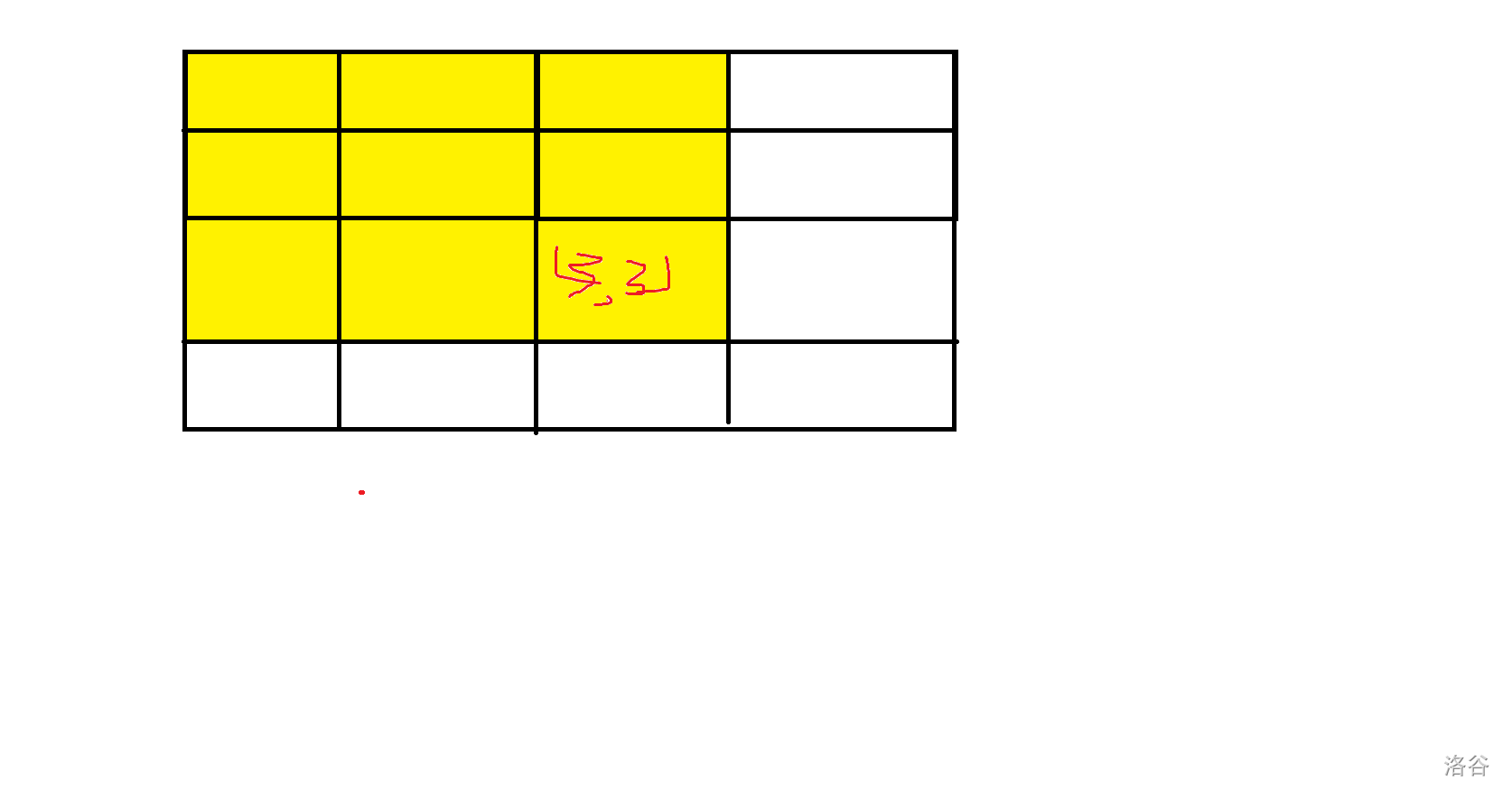： 黄色部分的和即为 fsum[3][3]
公式：fsum[i][j]=fsum[i-1][j]+fsum[i][j-1]-fsum[i-1][j-1]+a[i][j];
3.差分公式：cf[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1];
4.更改思路：

 

 完结撒花✿✿ヽ(°▽°)ノ✿

标签：前缀,公式,fsum,差分,二维,数组
From： https://www.cnblogs.com/wYYSZL/p/16750880.html