深度优先搜索(DFS)
引入:迷宫问题
有一个 \(n \times m\) 的迷宫,你一开始在 \((1,1)\),每次可以向上下左右走一步,要走到 \((n,n)\) 且路径不能重复,不能经过障碍,问有多少种方法?
用以下迷宫为例:
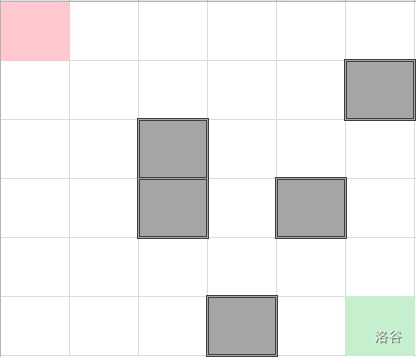
(红色是起点,绿色是终点)
我们每次可以向上下左右走一步。这样,我们每次选择一个方向,沿着这个方向走一步。
比如我们先向右走一步(目前在 * 处):
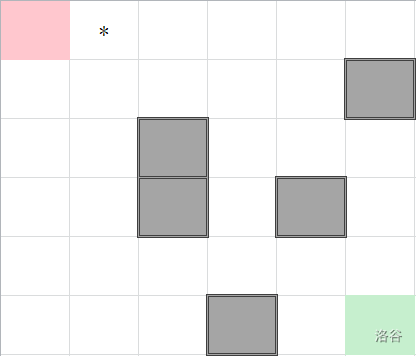
迭代加深搜索(IDS)
它本质上是一种对 DFS 的优化,在每次进行 DFS 的时候加上一个限制搜索深度的值 \(dep\),搜索到当前深度没找到解就直接返回,\(dep\) 加上 \(1\),继续搜索。
伪代码:
IDS(u,d)
if d>dep
return
else
for each edge (u,v)
IDS(v,d+1)
return
IDS 常用于找最优解。但是为啥不用 BFS 找最优解呢?
看这道题目:
例 P1763 埃及分数
如果我们使用 DFS,由于我们不知道答案有几个分数,所以搜索树的深度为无限深;如果使用 BFS,由于一个状态可以扩展到无数个状态,所以搜索树的宽度也为无限大,所以无法使用 DFS 和 BFS。
所以我们需要使用 IDS 来解决本题。
枚举搜索深度 \(dep\) 即为分解分数个数,同时为了避免重复状态,我们枚举到的后一个分数要比前一个分数小。
但是就这样显然是会被卡的,所以我们需要一波剪枝来优化一下。
我们不难注意到每次选取的分数一定不大于 \(\frac{x}{y}\)。
也就是说 \(y < x \times i\)。
这样就可以 AC 掉本题了。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll a,b,dep,ans[2001],now[2001];
bool found;
void do_frac(ll &a,ll &b){
int t=__gcd(a,b);
a/=t;
b/=t;
}
void ids(ll x,ll p,ll A,ll B){
ll a=A,b=B;
do_frac(a,b);
if(x==1){
if(a==1&&b>p){
if(found&&b>=ans[1]){
return ;
}
now[1]=b;
found=1;
memcpy(ans,now,(dep+1)<<3);
return;
}
return ;
}
int t=ceil(b*x*1.0/a*1.0);
for(int i=p;i<=t;i++){
now[x]=i;
ids(x-1,i,a*i-b,b*i);
}
return ;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>a>>b;
while(!found){
ids(dep,1,a,b);
dep++;
}
for(int i=dep-1;i>=1;i--){
cout<<ans[i]<<" ";
}
return 0;
}
A*
A* 算法是一种启发式搜索。
A* 是一种在图形平面上,对于有多个节点的路径求出最低通过成本的算法。它属于图遍历和最佳优先搜索算法。(in oi-wiki)
A* 其实是在 BFS 上加一个估价函数得到的。
我们令 \(g(u)\) 为从起点走到 \(u\) 的实际代价。
\(h(u)\) 为从 \(u\) 走到终点的预估代价。
那么 \(g(u)+h(u)\) 的意义即为从起点到终点,经过 \(u\) 的预估代价。
那么我们可以把 BFS 的队列变为优先队列,将 \(g(u)+h(u)\) 小的点优先扩展,因为这一类点最有可能扩展出终点。
然后再加一个 map 判重复状态即可。
例 P1379 八数码难题
考虑使用 A* 算法。
定义一个状态结构体,包含一个矩阵成员和一个步数成员。
重载该结构体的小于运算符为步数+估值函数是否大于另一个步数+估值函数。
然后不难想到估值函数为当前状态与目标状态有多少个格子不同。
但是此时会有个问题。
考虑以下情况:
123
840
765
此时我们的估值函数算出来是 \(2\),可是显然只需一步即可完成。
所以我们在计算估值函数的时候需要忽略空格的情况,否则会 WA 一个点(别问我怎么知道的)。
矩阵状态判重我使用的是矩阵哈希。
代码如下:
#include<bits/stdc++.h>
#define ll long long long
#define ull unsigned long long
#define mkp make_pair
using namespace std;
const int p=131;
struct matrix{
int a[4][4];
pair<int,int> find(){
for(int i=1;i<=3;i++){
for(int j=1;j<=3;j++){
if(a[i][j]==0) return mkp(i,j);
}
}
}
bool operator <(matrix x){
int cnt1=0,cnt2=0;
for(int i=1;i<=3;i++){
for(int j=1;j<=3;j++){
if(a[i][j]!=x.a[i][j]) return a[i][j]<x.a[i][j];
}
}
}
void debug(){
for(int i=1;i<=3;i++){
for(int j=1;j<=3;j++){
cout<<a[i][j];
}
cout<<endl;
}
cout<<endl;
}
}f,st;
int dx[]={0,0,0,1,-1};
int dy[]={0,1,-1,0,0};
int h(matrix x){
int cnt=0;
for(int i=1;i<=3;i++){
for(int j=1;j<=3;j++){
if(x.a[i][j]!=st.a[i][j]&&x.a[i][j]!=0){
cnt++;
}
}
}
return cnt;
}
ull get_hash(matrix x){
int cnt=0;
ull sum=0;
for(int i=1;i<=3;i++){
for(int j=1;j<=3;j++){
cnt++;
//cout<<sum<<" ";
sum+=x.a[i][j]*(ull)(pow(p,cnt));
}
}
return sum;
}
struct node{
matrix a;
int t;
bool operator<(node x) const{
return t+h(a)>x.t+h(x.a);
}
};
priority_queue<node> q;
map<ull,int> m;
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
st.a[1][1]=1;
st.a[1][2]=2;
st.a[1][3]=3;
st.a[2][1]=8;
st.a[2][2]=0;
st.a[2][3]=4;
st.a[3][1]=7;
st.a[3][2]=6;
st.a[3][3]=5;
for(int i=1;i<=3;i++){
for(int j=1;j<=3;j++){
char c=getchar();
f.a[i][j]=c-'0';
}
}
q.push((node){f,0});
m[get_hash(f)]=1;
while(q.size()){
matrix t1=q.top().a;
int t2=q.top().t;
q.pop();
if(h(t1)==0){
cout<<t2;
return 0;
}
int x=t1.find().first,y=t1.find().second;
for(int i=1;i<=4;i++){
//cout<<i<<endl;
int nx=x+dx[i],ny=y+dy[i];
if(nx&&ny&&nx<=3&&ny<=3){
swap(t1.a[x][y],t1.a[nx][ny]);
ull hs=get_hash(t1);
//t1.debug();
//cout<<" "<<hs<<" "<<m[hs]<<endl;
if(m[hs]==0){
//cout<<"added"<<endl;
m[hs]=1;
q.push((node){t1,t2+1});
}
swap(t1.a[x][y],t1.a[nx][ny]);
}
}
}
//cout<<"End";
return 0;
}
启发式迭代加深搜索 (IDA*)
我们在迭代加深搜索的时候,可以利用上 A* 算法的估值函数进行有效剪枝。
如果当前的步数+估值函数预估的最少步数大于我们限制的步数,则可以直接剪枝。
但是注意,这里的估值函数必须是乐观估计,否则可能会剪掉正解。
例题:P2324 骑士精神
这题可以使用 IDA*。
首先我们还是保存一个目标状态,还有一个方向数组。然后按 IDS 的方式写就是了。
估价函数跟八数码一样,算不一样的格子数 (除空格外)。
然后在进行递归的时候判断一下,如果符合要求就递归。
代码:
#include<bits/stdc++.h>
#define ll long long
#define debug
using namespace std;
int st[6][6]={
{0,0,0,0,0,0},
{0,1,1,1,1,1},
{0,0,1,1,1,1},
{0,0,0,2,1,1},
{0,0,0,0,0,1},
{0,0,0,0,0,0}};
int dx[]={0,1,1,-1,-1,2,2,-2,-2};
int dy[]={0,2,-2,2,-2,1,-1,1,-1};
int a[6][6];
bool found;
int h(){
int cnt=0;
for(int i=1;i<=5;i++){
for(int j=1;j<=5;j++){
if(a[i][j]!=st[i][j]&&a[i][j]!=2){
cnt++;
}
}
}
return cnt;
}
void ids(int dep,int nowdep,int x,int y){
if(dep==nowdep){
if(!h()) found=1;
return ;
}
for(int i=1;i<=8;i++){
int nx=x+dx[i],ny=y+dy[i];
if(nx>=1&&ny>=1&&nx<=5&&ny<=5){
swap(a[x][y],a[nx][ny]);
if(h()+nowdep<=dep){
ids(dep,nowdep+1,nx,ny);
}
swap(a[x][y],a[nx][ny]);
}
}
}
int t;
int main(){
cin>>t;
while(t--){
int x,y;
for(int i=1;i<=5;i++){
for(int j=1;j<=5;j++){
char c;
cin>>c;
if(c=='*'){
a[i][j]=2;
x=i,y=j;
}
else{
a[i][j]=(int)(c-'0');
}
}
}
if(h()==0){
puts("0");
goto luqyou;
}
for(int i=1;i<=15;i++){
ids(i,0,x,y);
if(found){
cout<<i<<endl;
goto luqyou;
}
}
puts("-1");
luqyou:;
found=0;
}
return 0;
}
这个代码吸氧可以过,不吸氧只有 90pts。