P3533 [POI2012] RAN-Rendezvous
题目大意:给定外向树森林,每次给定两个起始点,求两个点沿边移动最少步数相遇。
\(n\) 个点,\(n\) 条边,并且每个点有唯一的出边,显然构成了多棵基环树,对于每个基环树分别处理:找出环上的点,因为要求支持求出任意两点距离,前缀和一下即可。
对于询问,如果在两棵不同的基环树上(具体判断使用并查集),那么一定无解。如果在一棵基环树的同一棵子树内,求 LCA 并记录一下深度即可求出,代码实现使用的倍增。对于剩下的情况,进行分讨:
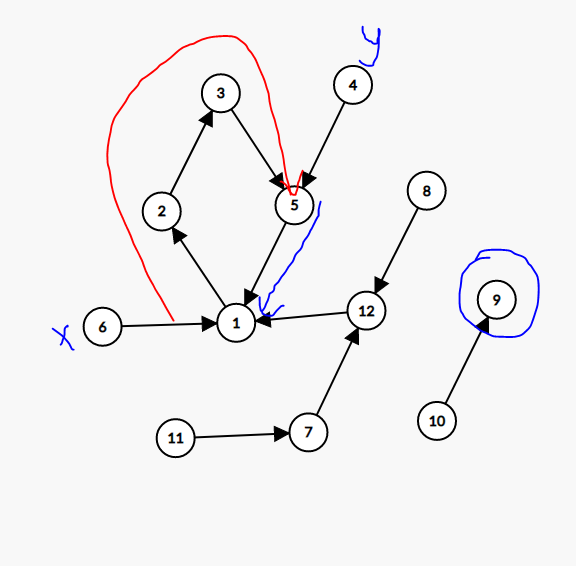
首先肯定是要花 \(dep-1\) 步走到环上,接下来有两种选择:从 \(top_x\) 走到 \(top_y\) 或者从 \(top_y\) 走到 \(top_x\)。具体的,我们给 \(1,2,3,5\) 赋权值为 \(1,2,3,4\) 红色的距离就是 \(4-1=3\),蓝色的距离是 \(1-4+4\) 加 \(4\) 是因为正好越过了整个环。
感觉思维难度完全到不了紫,实现稍微麻烦一点,遵循题目中的条件,判断自环等特殊情况,一定要注意判断环的方向!
int n,q,cnt=1,flag,tot,f[1000001],loop[1000001],val[1000001],maxn[1000001],vis[1000001],a[1000001],dis[1000001],head[1000001],to[1000001],nex[1000001],dep[1000001],fa[1000001][31],top[1000001];
inline void add(int x,int y){to[++cnt]=y,nex[cnt]=head[x],head[x]=cnt;}
stack<int> st;
void dfs(int k,int from)
{
vis[k]=1,!flag?st.e(k),1:1;
for(int i=head[k];i;i=nex[i])
{
if(i==(from^1))continue;
if(!flag&&vis[to[i]])
{
while(st.top()!=to[i])loop[++tot]=st.top(),st.pop();
loop[++tot]=st.top(),st.pop(),flag=1;
while(!st.empty())st.pop();
}
if(!vis[to[i]])dfs(to[i],i);
}
!flag?st.pop(),1:1;
}
void dfs2(int k,int father)
{
top[k]=top[father],dep[k]=dep[father]+1,fa[k][0]=father;
for(int i=1;i<=30;++i)fa[k][i]=fa[fa[k][i-1]][i-1];
for(int i=head[k];i;i=nex[i])if(vis[to[i]]==1&&to[i]!=father)dfs2(to[i],k);
}
inline int LCA(int x,int y)
{
if(dep[x]>dep[y])swap(x,y);
for(int i=30;i>=0;--i)if(dep[fa[y][i]]>=dep[x])y=fa[y][i];
for(int i=30;i>=0;--i)if(fa[y][i]!=fa[x][i])y=fa[y][i],x=fa[x][i];
return x==y?x:fa[x][0];
}
int find(int x){return x==f[x]?x:f[x]=find(f[x]);}
inline void mian()
{
read(n,q);int x,y,z,lca,t,w;
for(int i=1;i<=n;++i)f[i]=i;
for(int i=1;i<=n;++i)read(a[i]),add(i,a[i]),add(a[i],i),f[find(a[i])]=find(i);
for(int i=1;i<=n;++i)
{
if(vis[i])continue;
flag=tot=0,dfs(i,0);
if(a[loop[1]]!=loop[2])reverse(loop+1,loop+1+tot);
for(int j=1;j<=tot;++j)vis[loop[j]]=2;
for(int j=1;j<=tot;++j)maxn[loop[j]]=tot,val[loop[j]]=val[loop[j-1]]+1,top[0]=loop[j],dfs2(loop[j],0);
}
while(q--)
{
read(x,y);
if(find(x)!=find(y)){puts("-1 -1");continue;}
if(top[x]==top[y])lca=LCA(x,y),write(dep[x]-dep[lca]),write(dep[y]-dep[lca],'\n');
else
{
z=val[top[y]]-val[top[x]];if(z<0)z+=maxn[top[x]];
t=val[top[x]]-val[top[y]];if(t<0)t+=maxn[top[x]];
if(max(dep[x]-1+z,dep[y]-1)< max(dep[y]-1+t,dep[x]-1)
|| max(dep[x]-1+z,dep[y]-1)==max(dep[y]-1+t,dep[x]-1)&&min(dep[x]-1+z,dep[y]-1)< min(dep[y]-1+t,dep[x]-1)
|| max(dep[x]-1+z,dep[y]-1)==max(dep[y]-1+t,dep[x]-1)&&min(dep[x]-1+z,dep[y]-1)==min(dep[y]-1+t,dep[x]-1)&&dep[x]-1+z>=dep[y]-1)write(dep[x]-1+z),write(dep[y]-1,'\n');
else write(dep[x]-1),write(dep[y]-1+t,'\n');
}
}
}