2023-08-28 15:53:53
$$A$$
典型错误
一知半解看样例型:
- 如果该队某个数组的值比最大值大就算入答案。
上第一次厕所前我的思路:开局 \(30\) 分钟。
显然,我并不需要有一个数值最大才能赢,我只需要其中一个数值比 其中一个数值比 其中一个数值最大的那个 要大的队 要大即有可能获胜。(可以通过断句来理解)
看懂了但是没有完全理解,且没有深度分析大样例型:
- 一个球队必输:当且仅当存在一个队伍,其每个属性都比它高。
上了第一次厕所后:开局第 \(30 \sim 100\) 分钟我一直把这个当作真理去打,就去找统计被淘汰的队伍数,结果发现大样例完全过不了。这时才分析大样例的 \(i=8\) 才发现,就算我所有数值都比一个组高,那个组还是可以通过打败可能打败我的组来获得胜利,因此这个策略错误。
正解
我苦思冥想,又上了一次厕所,然后在机房里散步(被吐槽了),在桌子上坐着。
然后想到了并查集合并。
发现了可以把每一个数值的上下界看作线段维护之后,很【容易想到用并查集维护 \(k\) 条线段构成的一个二维区间。我们用并查集维护每一个组的数量(顺便写个按秩合并),然后想什么情况合并——很简单,只要二维区间有交就合并。最后答案就是任意一个属性最大的那个区间(为什么?因为不会有交,所以每个集合之间相互独立,不可能出现一个值比一个组大,另外一个小于的情况,否则早被合并了)。
可能不太好理解,结合代码理解一下?
其实这道题跟并查集没有任何关系,只是我想用并查集写而已,关键在合并操作,而不是并查集。复杂度本来感觉过不了的啊,应该是没有把我卡掉的数据吧,大样例放洛谷上跑了 \(200ms\) 左右吧?
\(Code\)
#include<bits/stdc++.h>
using namespace std;
int read(){
int x=0;char c=getchar();
for(;!isdigit(c);c=getchar());
for(;isdigit(c);c=getchar())x=(x<<3)+(x<<1)+(c^48);
return x;
}
struct line{
int u,d;
}a[6][100005];
int n,m,fa[100005],siz[100005];
unordered_set<int>S;
inline int find(int x){
if(x==fa[x])return x;
return fa[x]=find(fa[x]);
}
int merge(int x,int y){//合并操作
if((x=find(x))==(y=find(y)))return y;
if(siz[x]>siz[y])swap(x,y);
for(int i=1;i<=m;i++){
a[i][y].u=max(a[i][y].u,a[i][x].u);
a[i][y].d=min(a[i][y].d,a[i][x].d);
}
fa[x]=y,siz[y]+=siz[x],siz[x]=0;
return y;
}
bool check(int x,int y){//判断能不能合并
bool up=0,down=0;
x=find(x),y=find(y);
for(int i=1;i<=m;i++){
if(a[i][x].u<a[i][y].d)down=1;
if(a[i][x].d>a[i][y].u)up=1;
if(a[i][x].d<a[i][y].u&&a[i][x].u>a[i][y].u)return 1;
if(a[i][x].d<a[i][y].d&&a[i][x].u>a[i][y].d)return 1;
if(a[i][y].d<a[i][x].u&&a[i][y].u>a[i][x].u)return 1;
if(a[i][y].d<a[i][x].d&&a[i][y].u>a[i][x].d)return 1;
}
return up&down;
}
queue<int>Q;
int main(){
n=read(),m=read();
if(m==1){//不加这个可能就只有 90,m=1 我就退化到 O(n^2) 了
for(int i=1;i<=n;i++)
printf("1 ");
return 0;
}
for(int i=1;i<=n;i++){//预处理
fa[i]=i;siz[i]=1;
for(int j=1;j<=m;j++){
a[j][i].u=a[j][i].d=read();
}
}
for(int i=1;i<=n;i++){
int x=i,maxx=0,ans;
for(int y:S){
if(!check(x,y))continue;
Q.push(y);//直接删会本地就会报错,不知道为什么
x=merge(x,y);
}
while(!Q.empty())S.erase(Q.front()),Q.pop();//拿出来删就好了,不差这点复杂度
S.insert(x);
for(int y:S){
if(a[1][y].d>=maxx)maxx=a[1][y].d,ans=siz[y];//找最大的(这复杂度不爆???)
}
printf("%d ",ans);
}
}
发完以后有人说完全看不懂,那我就结合图片讲一下?
我们把每个队各个属性的数值看成纵坐标,属性的编号看成横坐标,那么我们可以得到以这一个坐标图。
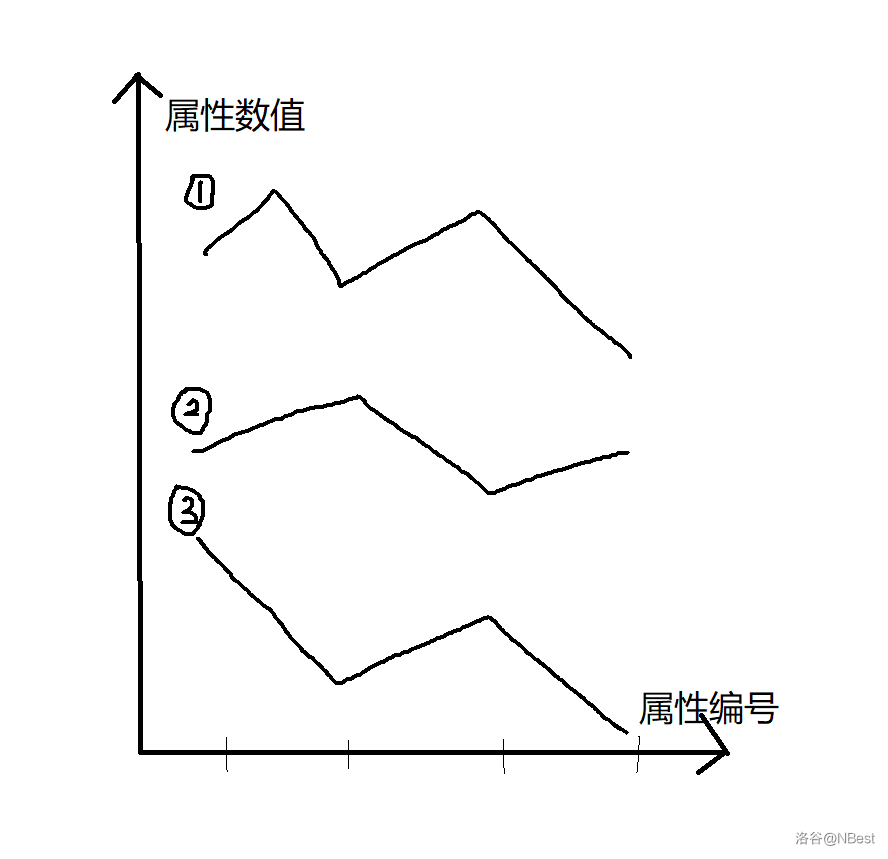
此时他们之间互不相交,彼此之间都是绝对碾压无法超过的关系,那么显然 1 就是冠军。
那此时我们加入一个 4?
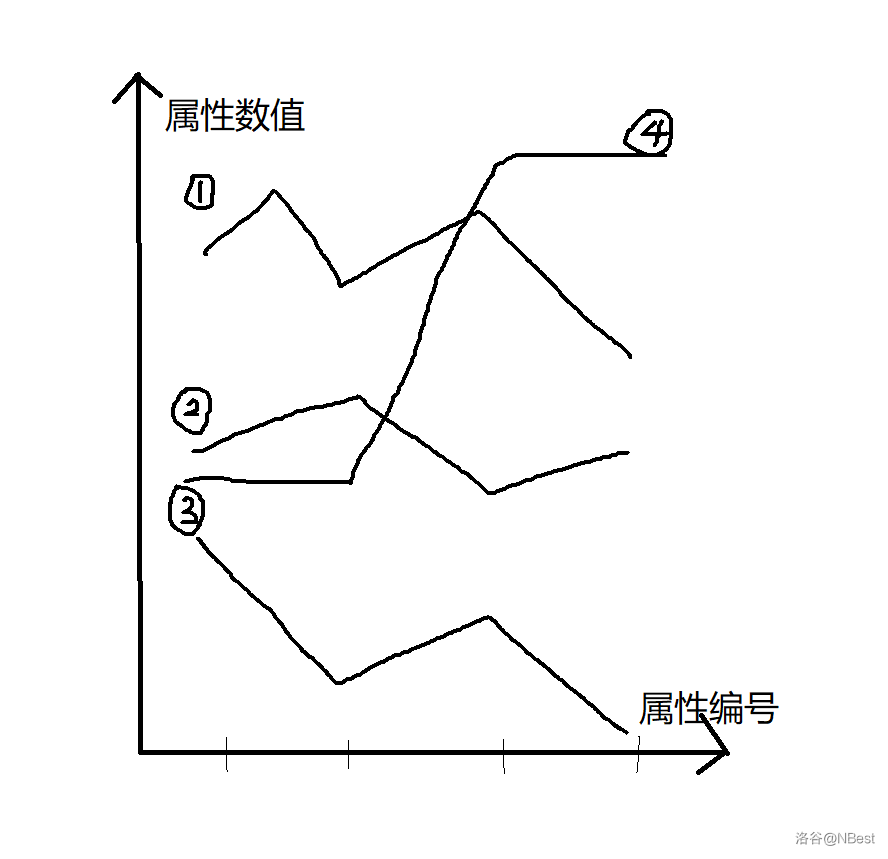
此时 1 和 4 可以互相打过,那么 2 只需要在 4 打败 1 之后打败 4,那 2 也能成为冠军,那么此时可能的冠军就变成了 1,2,4。
此时 3 如果争气一点,找到一个可能打过 1,2,4 其中一个的队然后战胜它,那么 3 也能成为冠军,那么我们假设这个点是 5,因为需要 3 打过 5,那么 5 至少一个数值比 3 小,又得 5 打过 1,2,4 那么 5 必然跟 1,2,4 三条线构成的图有交。
那么就可以得到结论了,只要两个图形有交就合并,最后取其中一个数值最大的图形的大小即为答案。
B
是一个很烦的模拟题,我不想打,所以就暂且跳了吧(挖坑)。
C
题意:
给定一个 \(n\times m\) 的 \(01\) 数组,你可以同时翻转一行或者一列的状态 (\(1\)->\(0\),\(0\)->\(1\)),问翻转任意次后最少能有几个 \(1\)。
\(n\le 20,m\le 10^5\),时限 6000ms。
看到 \(n\) 这么小,我们想到朴素的贪心加暴力。
关注到我们如果选定了翻的一些行和列,那么其翻转的顺序不会对最终答案造成影响,而且同一行或者列翻多次没有意义。
所以我们可以考虑 \(O(2^n)\) 枚举行的翻转状态,然后贪心看每列要不要翻,复杂度 \(O(nm2^n)\),优化一下可以跑 \(n\le15,m\le1000\) 的 \(60\) 部分分。
\(60pts\ Code\)
int n,m,ans=1e9;
bool a[20][100005],vis[20];
void dfs(int x){
if(x>n){
int res=0;
for(int j=1;j<=m;j++){
int p=0;
for(int i=1;i<=n;i++){
if(vis[i])p+=a[i][j]^1;
else p+=a[i][j];
}
res+=min(p,n-p);
if(res>ans)return;//优化
}
ans=res;
return;
}
dfs(x+1);
vis[x]=1;
dfs(x+1);
vis[x]=0;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
string l;
cin>>l;
for(int j=0;j<m;j++){
a[i][j+1]=l[j]^48;
}
}
dfs(1);
cout<<ans;
}
考虑正解。
这题可以用两个方法——dp或者FWT。这里先讲一下 dp,虽然复杂度多了一个 \(n\),但是毕竟前置知识少,所以方便写(可能不太好想到?毕竟当时好像CF赛时 tourist 都没打出来)。
注意到,每一列的很多状态很多都是重复的,而我们最终的答案相当于我们在一个全 0 的序列中翻转了一些数使得其变成了 1,求最少翻转次数。那最终我们只需要通过翻转和单点修改让每一列的状态即可,答案即为最小单点修改次数。
我们令 \(f_{i,s}\) 表示通过 \(i\) 次不重复单点修改变成状态 \(s\) 的列数。
最后答案就是枚举状态 \(s\),把对应的次数和数量相乘取最小值即可,复杂度 \(O(n^22^n)\)。
int n,m,zt[100000],f[21][1<<20];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
string l;cin>>l;
for(int j=0;j<m;j++)
zt[j]=(zt[j]<<1)+(l[j]^48);//计算列状态
}
for(int i=0;i<m;i++)
f[0][zt[i]]++;//状态计数
for(int k=0;k<n;k++)//注意循环顺序,因为不能重复翻一个点,所以最外层枚举翻的点
for(int i=k+1;i;--i)//常数优化,减少无用状态转移,同时注意从大到小,也是防止翻同一个点
for(int j=0;j<(1<<n);j++)
f[i][j]+=f[i-1][j^(1<<k)];
int ans=2000000;
for(int i=0;i<(1<<n);i++){//枚举最后所有列的状态
int res=0;
for(int j=0;j<=n;j++){
res+=f[j][i]*min(j,n-j);//翻转了的答案和没翻转的取最小值
}
ans=min(ans,res);
}
cout<<ans;
return 0;
}
FWT 做法
不想学 FWT,推个式子吧。
xor_FWT 运用:
给定长度为 \(2^n\) 两个序列 \(A,B\),设
\[C_i=\sum_{j\oplus k = i}A_j \times B_k \]可以在 \(O(n2^n)\) 里求出 \(C\) 序列。
设翻转行的二进制操作序列为 \(opt\),\(S_i\) 为第 \(i\) 列翻转前的序列,\(T_i\) 为翻转后的序列,不能得到 \(T_i=S_i\oplus opt\)。
根据我们一开始的贪心思路,第 \(i\) 列对答案的贡献 \(ANS(T_i)=min\{popcount(T_i),n-popcount(T_i)\}\)。
那么最终答案 \(ans\) 可以表示为:
\[\large\begin{aligned}ans&=\min_{opt}\sum_{i=1}^{m}ANS(S_i\oplus opt)\end{aligned} \]复杂度 \(O(m2^n)\)。
用 \(W(S)\) 表示状态为 \(S\) 的个数,那么:
\[\large\begin{aligned}ans&=\min_{opt}\sum_{S}ANS(S\oplus opt)\times W(S)\\&=\min_{opt}\sum_{S\oplus T=opt}ANS(T)\times W(S)\end{aligned} \]然后就变成 xor_FWT 问题了,也就是在 \(C\) 序列里面找最小值。
D
题意:
给定一颗树,每条边的边权为 \(a+b\times delta\),问你当 \(delta\in[0,lim]\) 时,树的最小直径,并求出取到最小直径时的最小 \(delta\)。
\(n\le 2.5\times 10^5,lim \le10^6,|a_i|\le10^8,|b_i|\le10^3\)。
做法
D 好水啊,一开始没发现,暴力都没打,主要是因为之前上课都没听,不知道怎么求树的直径,然后看到要求直径就直接 skip 了。
这显然是个二分/三分题,我们把树上每条路径都拿出来,发现对于每条路径的长度,都是关于 \(delta\) 的一次函数,然后我们把这些直线放到图上,大概是长这样的:
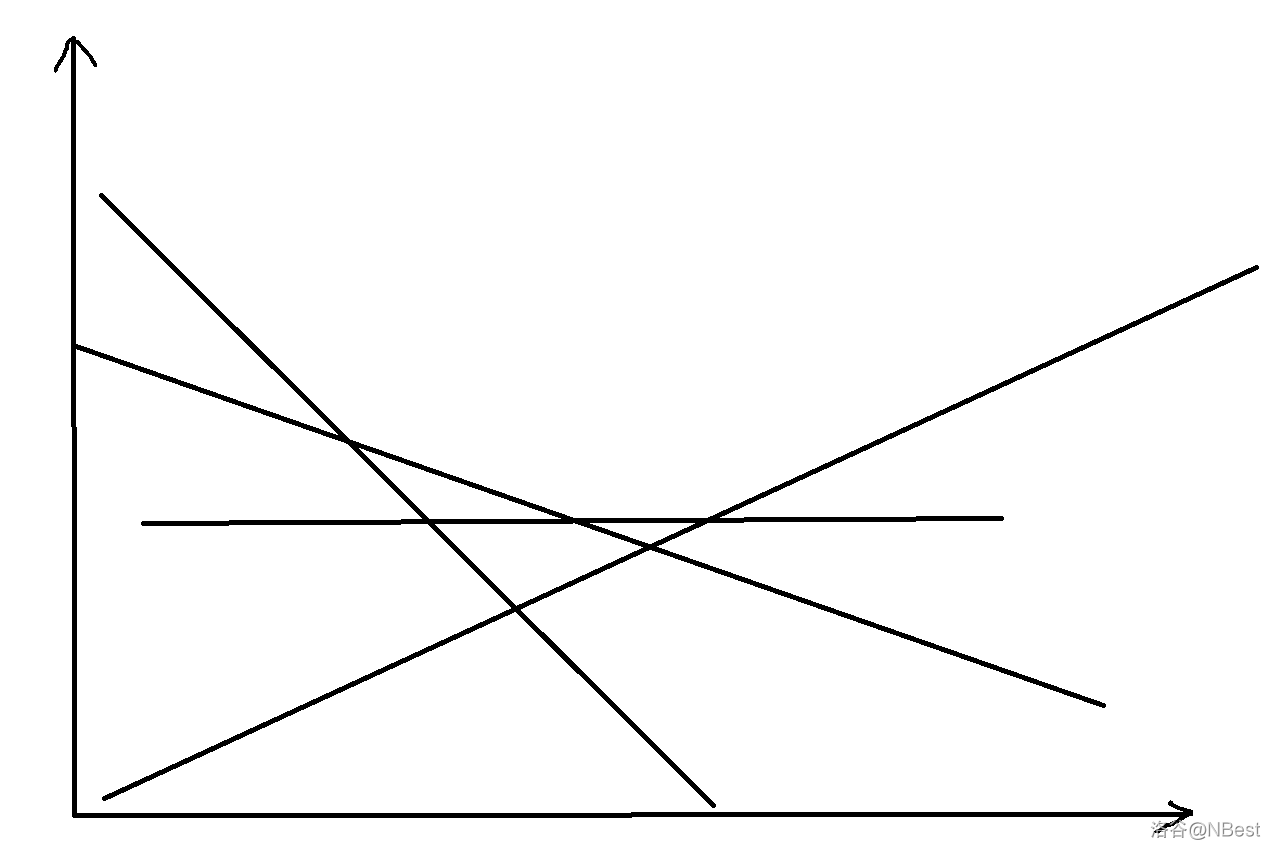
(横坐标是 \(delta\),纵坐标是路径长度)
直径就是最长的路径,所以我们对这些线取个 \(max\),发现得到了一个半凸包(不知道是不是这么叫)。
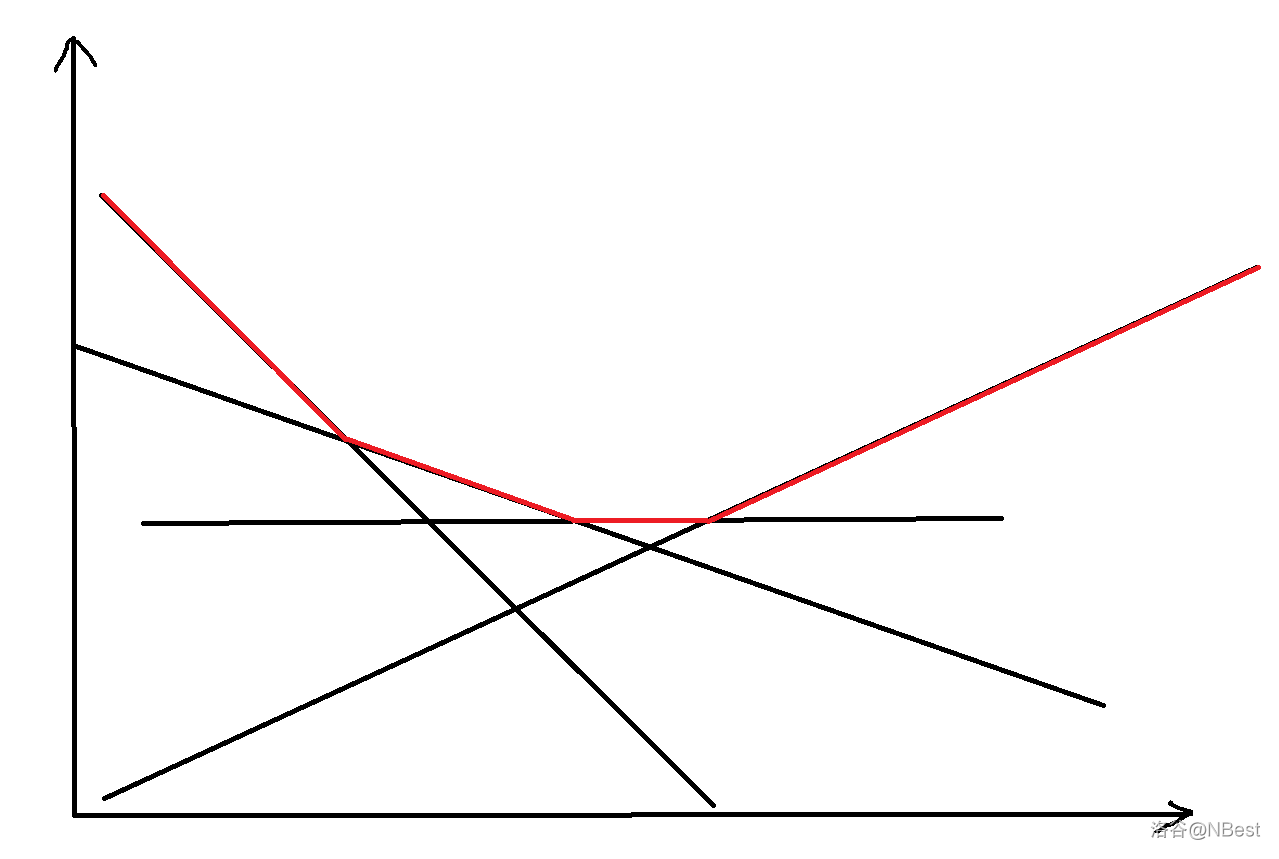
显然不管怎样放都是一个类似单峰的折线,所以我们直接对答案进行三分就行了,三分可以参考题目:P3382 三分法。
可是其实不需要像三分模板那样取三等分点,直接取中点然后比较 \(mid\) 和 \(mid+1\) 代入函数的关系:
- 如果 \(cal(mid)<=cal(mid+1)\),那么 \(mid+1\) 一定在答案的右侧,所以我们缩小范围时就不需要 \(mid+1\) 了,直接令 \(r=mid\) 即可。
- 如果 \(cal(mid)>cal(mid+1)\),那么发现 \(mid\) 一定不是答案,且 \(mid\) 一定在答案右侧,因此令 \(l=mid+1\) 即可。
怎么算直径呢?
树的直径通常有两种求法——搜素和树形 dp,我个人更偏向选择树形 dp 的做法,因为不仅只需要跑一遍 dfs,而且就算有负权也能保证求出正确答案。
这是因为跑两遍搜索的原理是从一点出发找到它的最长路的结束点,然后再用这个最长路的结束点去更新答案,这样做保证正确只能当没有负权边的时候成立。
证明给出:
先假设没有负权边。
我们假设从 \(A\) 点出发,能到的最远点是 \(D\) 点,而此时的直径是 \(B-C\)。
情况 1:当 \(A-D\) 和 \(B-C\) 不相交
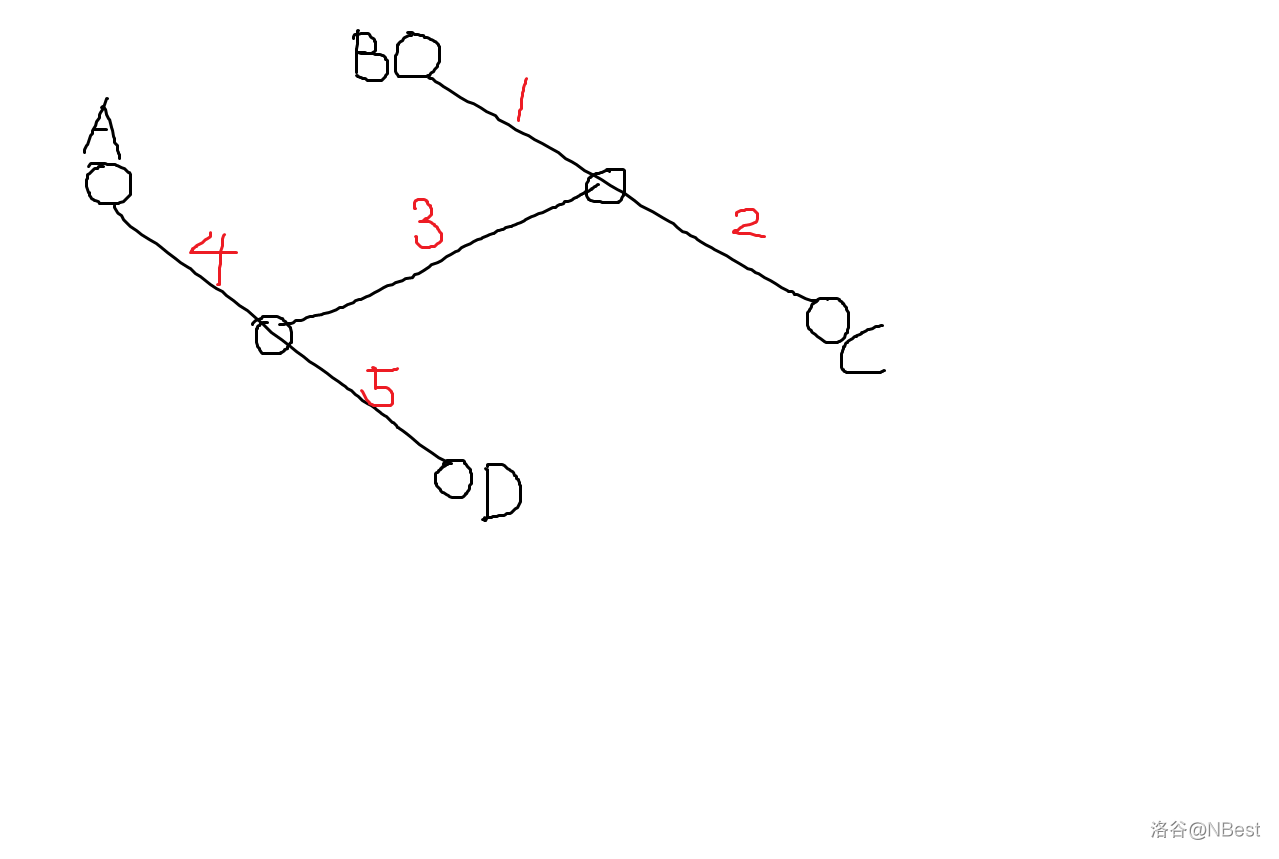
因为 \(A\) 的最长路到的是 \(D\),所以显然 \(path:4+5\ge4+3+2\iff path:5\ge 3+2\)。
如果 \(3\) 是非负路,那么一定有 \(path:1+3+5\ge 1+2\)。
那么此时直径可以为 \(B-D\)。
情况 2:当 \(A-D\) 和 \(B-C\) 相交
这个更好证明:
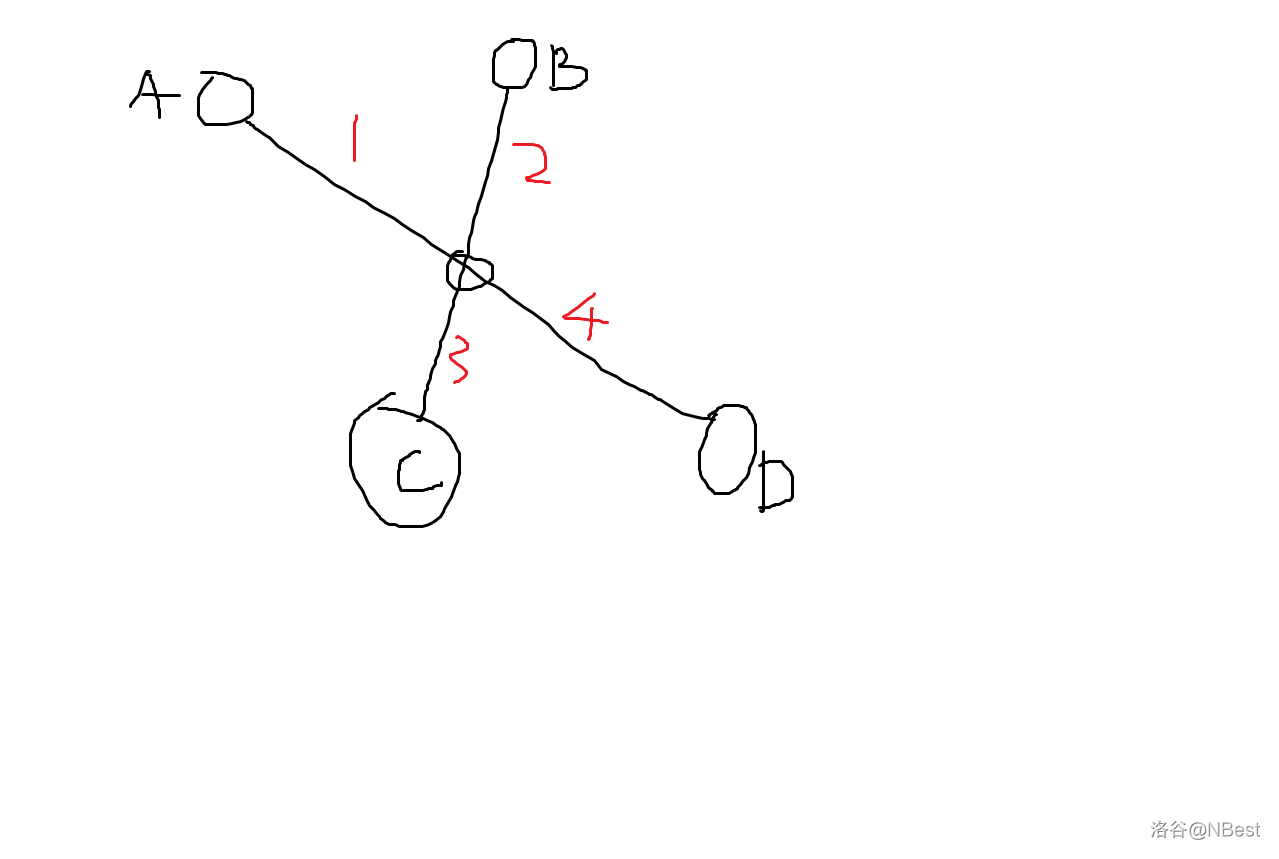
这个不用管是不是负权边,肯定有 \(path:1+4\ge 1+3\iff path: 2+4\ge 2+3\),所以 \(B-D\) 为不劣解。
树形 dp 求直径
而这个题的权值可能为负数,所以显然不能两次搜素法,那就打一个简单的树形 dp 即可。
令 \(f_x\) 表示以 \(x\) 为子树的根,到子树的最长路,那么我们只要边更新 \(f_x\) 边算直径即可。
void dfs(int x,int fa){
for(auto PI:F[x]){
int y=PI.to;ll w=PI.v;
if(y==fa)continue;
dfs(y,x,v);
len=max(len,f[x]+f[y]+w);//此时 f[x]还没有被更新,因此是与其他子树的最长路
//那么包含 x 的最长路径就可以通过找最长和次长的路更新,再贡献到直径答案中。
f[x]=max(f[x],f[y]+w);//更新答案
}
}
然后就做完了。
\(Code\)
struct edge{
int to;ll a,b;
inline ll v(ll w){return a+b*w;}
};
int n;
vector<edge>F[250004];
ll f[250004],len,lim;
void dfs(int x,int fa,ll v){
for(auto PI:F[x]){
int y=PI.to;ll w=PI.v(v);
if(y==fa)continue;
dfs(y,x,v);
len=max(len,f[x]+f[y]+w);
f[x]=max(f[x],f[y]+w);
}
}
ll cal(ll v){
memset(f,0,sizeof(f));
len=0;
dfs(1,0,v);
return len;
}
int main(){
n=read(),lim=read();
for(int i=1;i<n;i++){
int u=read(),v=read(),a=read(),b=read();
F[u].push_back({v,a,b});
F[v].push_back({u,a,b});
}
ll l=0,r=lim;
while(l<r){
ll mid=(l+r)>>1;
if(cal(mid)<=cal(mid+1))r=mid;
else l=mid+1;
}
printf("%lld\n%lld",l,cal(l));
}
总结:
玩原神玩多了。
太菜了,在如此秒的第一题上浪费了太久,没有写出如此秒的第四题。都是玩原神玩的太菜了。