带权并查集

普通的并查集只能维护每个节点所在集合的编号，带权并查集则可以维护集合内任意一点到所在集合根的距离。

带权并查集是结点存有权值信息的并查集。相比于一般的并查集，带权并查集需要开辟两个数组：一个是dsu[N]，用来判断集合关系；一个是dis[N]，用来描述其与根节点的关系。

当两个元素之间的关系可以量化，并且关系可以合并时，可以使用带权并查集来维护元素之间的关系。

带权并查集每个元素的权值通常描述其与并查集中祖先的关系，这种关系如何合并，路径压缩时就如何压缩。

带权并查集可以推算集合内点的关系，而一般并查集只能判断属于某个集合。

结论（带权并查集做题流程）：

首先看有没有类似并查集的用法，能不能通过集合的方式做题；接着看需不需要额外维护权值，如果要就要看两个东西：

• 合并的时候，权值如何运算。

  • 并查集的统一合并操作：合并a->b，就要找到a和b的父节点，然后在两个父节点之间连边，运算出来的结果就是这条边的权值。

• 查询的时候，如何得到所查节点的权值。

  • 知道两个节点到根节点的权值，如何得到两个节点之间的权值。

以下例题1是解释什么是带权并查集的。

例题1：

有一个长度为 N 的整数序列。

下面会按顺序给出 M 个对该序列的描述，每个描述给定三个整数 l,r,s，表示该序列的第 l 个元素至第 r 个元素相加之和为 s。

对于每个描述，你需要判断该描述是否会与前面提到的描述发生冲突，如果发生冲突，则认为该描述是错误的。

如果一个描述是错误的，则在对后续描述进行判断时，应当将其忽略。

请你计算一共有多少个描述是错误的。

输入格式

第一行包含两个整数 N,M。

接下来 M 行，每行包含三个整数 l,r,s，表示一个描述。

输出格式

一个整数，表示错误描述的数量。

带权并查集的解释：

dis[]表示某个节点到根节点的权值。

在这题的含义就是某个端点(节点)到另一个端点(根节点)所构成的区间的和，这里不需要管这两个点谁小谁大，因为权值可以是负数，最后计算的结果是没有影响的。

• 由这个dis数组，可以得到在同一个集合内，所有节点之间的权值。

初始化的时候，dis[]全为0，表示自己到自己的权值为0。

如何理解权值的合并：

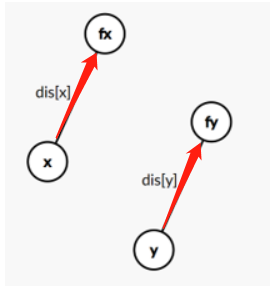
合并两个集合的操作，可以通过向量的方法来理解：dis数组用于记录节点到根节点的距离，然后每种关系如图所示，最终我们需要将fx接到fy上去，所以我们需要修改fx的权值，也就是向量fx->fy，如下图所示的向量计算。

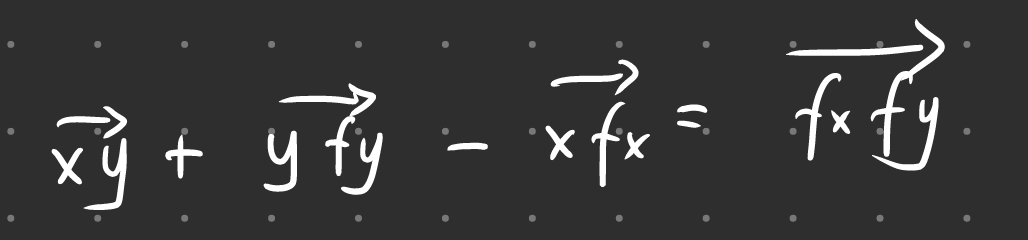
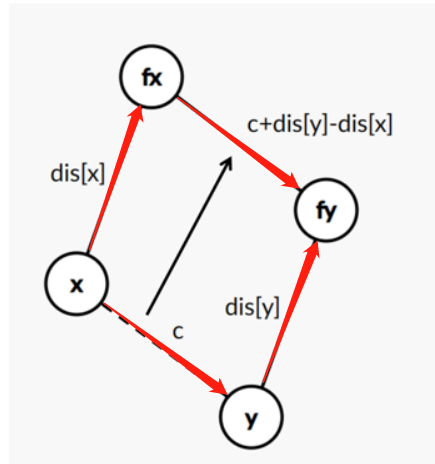
注意刚刚说的，dis所表示的权值可能是负数，如果用向量去理解，就很好理解：如下图所示，区间中蓝色和绿色的区间是已知的，然后现在需要添加 $(l_2,r]$ 或者说：($l_2$->r)，已经合并好的集合如下面所示，找到$l_2$的父节点$r_2$，r的父节点$r_1$，需要添加一条边$r_2$->$r_1$ 这时候就会发现，假如从左到右的箭头表示权值为正数，那么新加入的边权值居然变成了负数，但是最后是不影响计算的结果的（后面有解释）。

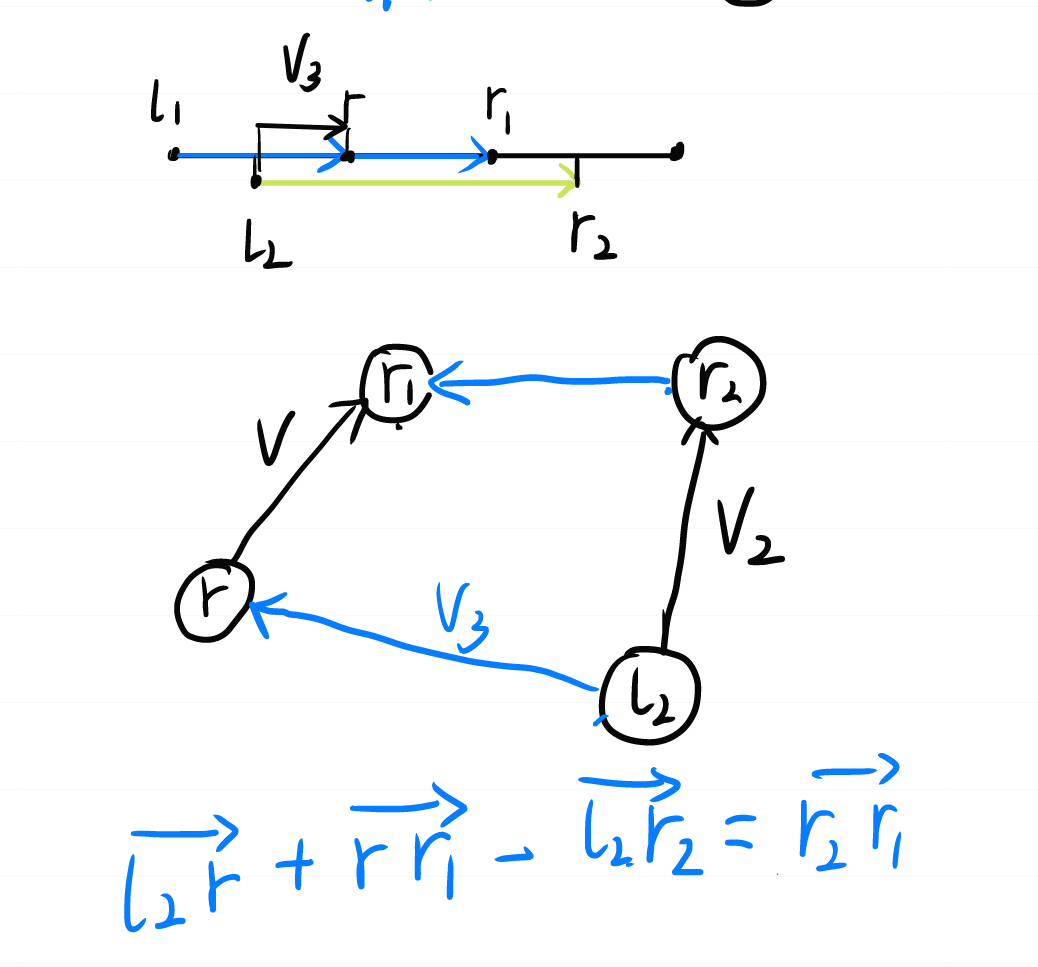
如果是询问节点间的权值是否为v，那么由于两个节点都在集合内，所以有共同的根节点，所以只要计算 $(l,rot) -(r,rot)$ 是不是等于v即可（向量的意思）

对前面负数权值的解释：比如，询问$r_1$->$r_2$ ，计算$(r_1,rot) 减(r_2,rot)$ ，$(r_1,rot)$中$r_1$就是根节点，所以是0； $(r_2,rot)$ 中rot是$r_1$ ,权值我们是知道的，就是$dis[r_2]$ ，所以最后的结果就是$0-dis[r_2]$ ，最后结果又变成了正数。

AcWing 4286. 多少个答案是错误的 - AcWing <-举例

注意！！！

针对本题，根据区间合并原理，我们将左端点-1处理成左开右闭区间，(0,3] + (3, 10] = (0,10] == [1,10].

因为，如果存的是闭区间[1,5]和[5,10]合并，5下标的数就会被算了两次,处理之后才可以直接通过三个点得到两个区间的关系--(0,5]应该和(5,10]区间合并，而不是[5,10]，[5,10]会被处理成(4,10]，也就是说前面说的两个区间是有重叠的。

#include <bits/stdc++.h>
using namespace std;

#define int long long
vector<int> dsu(200005);
vector<int> d(200005);//存权值，表示到根
int ans = 0;

int find(int x) {
    if (x != dsu[x]) {
        int rot = dsu[x];//记录父节点编号
        dsu[x] = find(dsu[x]);
        d[x] += d[rot];//从根节点开始回溯，把权值累加
    }
    return dsu[x];
}

void root(int x, int y, int v) {
    int x_ = find(x);//正常的并查集操作
    int y_ = find(y);
    if (x_ == y_) {
        ans += (d[x] - d[y] != v);
    } else {
        dsu[x_] = y_;//将x的根节点接到y的根节点上去
        d[x_] = v + d[y] - d[x];//修改权值
    }
}

signed main() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        dsu[i] = i;//初始化并查集
        d[i] = 0;//初始化权值
    }
    for (int i = 1; i <= m; i++) {
        int x, y, v;
        cin >> x >> y >> v;
       x--;//记得减一,处理为左开右闭区间
        root(x, y, v);
    }
    cout << ans << endl;
}

240. 食物链 - AcWing题库

#include <bits/stdc++.h>
using namespace std;

vector<int> dsu(500005);
vector<int> d(500005);
int ans ;
int find(int x) {
    if (x != dsu[x]) {
        int rot = dsu[x];
        dsu[x] = find(dsu[x]);
        d[x] = (d[rot] + d[x]) % 3;
    }
    return dsu[x];
}


void root(int x, int y, int v) {
    int x_ = find(x);
    int y_ = find(y);
    if (x_ == y_) {
       if(v != (d[x] - d[y] + 3) % 3){
            ans++;
       // cout << x << ' ' << y << ' ' << v << "?" << (d[x] - d[y] + 3) % 3 << endl;
       }
    } else {
        dsu[x_] = y_;
        d[x_] = (v + d[y] - d[x]) % 3;
    }
}

int main() {
    int n, t;
    cin >> n >> t;
    for (int i = 1; i <= n; i++) {
        dsu[i] = i;
    }
    for (int i = 1; i <= t; i++) {
        int tmp, x, y;
        cin >> tmp >> x >> y;
        if (tmp == 2 && x == y)
            ans++;
        else if (x > n || y > n)
            ans++;
        else {
            root(x, y, tmp - 1);
        }
       
    }
     cout << ans << endl;
}

AcWing 240. 食物链(带权并查集) - AcWing