spfa在使用中问题的简单分析

　　作者水平一般，有问题请指出，我将及时修改。
〇、问题引入
　　spfa 本质上是队列优化贝尔曼福特。我们可以使用队列，在每一轮的点更新中仅更新上一轮更新中的被更新点的相邻的点（好绕……）。这种情况下的算法复杂度与Dijkstra不相上下。

但是有一个问题，这么好的算法为什么没有被大量使用呢？

那必然是不玩原神导致的因为这种算法有很严重的缺陷。

一、算法比较 （spfa——Dijkstra）

　　纯净无杂质无优化的Dijkstra的算法复杂度为 $O($$n^2$$)$ ，加入少量杂质优化后可以达到 O((n+m) log n)。而spfa再怎么好也不会改变它复杂度高达 O(nm) 的现实。
这也就导致了在遇到像稠密图这种边巨多无比的这种情况，spfa很容易当场去世。
二、问题分析
1、简述过程
　　1. 初始化
　　2. 点入队，计算最短路，更新状态
　　3. 点出队，将其状态被改变的相邻点入队
　　4. 重复上述步骤
　　5. 如果队列为空，结束步骤4，当前答案点状态即为答案
2、拟似问题
　　经过分析，我们发现，某个点在更新完后，如果在后续的运算中发现它可以通过多走几个点来减少距离，比如这样：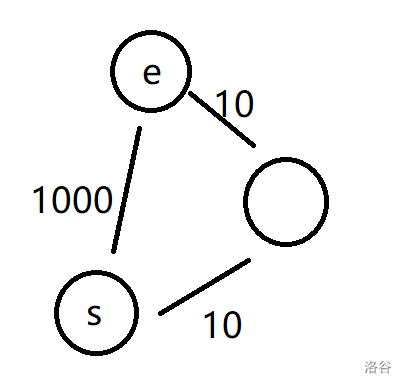
)
　　那么它就会再次被入队。这样的神奇小原因导致了spfa算法的复杂度被严重拉低，同一个点被重复入队一两次还好说，那如果每个点都被大量、重复地入队，那这个运算量就够咱吃一壶的了。比如下面这个bi图：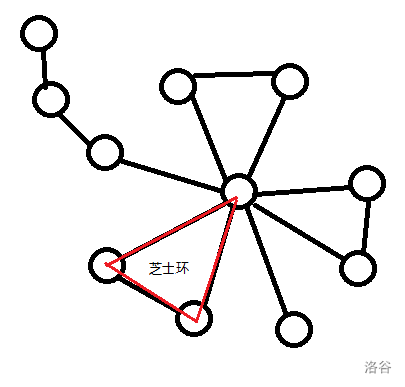
（理由是spfa会受环的影响将部分点一遍遍的刷新，重点是还没用！）
　　或者这个：
（理由是网格状的图会出现很多近似或者说就是最短路，消耗时间）

　　如果出题人整了个这样的上蹿下跳的莎比数据你总没治。

　　但是 spfa 并非一无是处，就像碰到带负权的题，你就不得不考虑一下spfa了（但是也未必用了一定对）。
最后介绍spfa的两个优化：酸辣粉优化（SLF）和拉拉链优化（LLL），但是我真的打不动了
三、个人建议
　　想不到吧，我根本没有建议可提！
四、啥也不是
　　贴一个使用了spfa的程序，该程序仅作参考

#include<bits/stdc++.h>
using namespace std;
const int maxn = 10001;
const long long INF = 2147483647;
int dis[maxn];//记录最小路径的数组
int vis[maxn];//标记
int n, m, s;
struct node {
    int s1;//记录结点
    int side;//边权
};
void init() {
    for (int i = 1; i <= n; i++) {
        dis[i] = INF;
        vis[i] = 0;
    }
}
vector<node>mp[maxn];//用vector建立邻接表
void Spfa(int s) {
    queue<int>v;   
    vis[s] = 1; v.push(s); dis[s] = 0;
    while (!v.empty()) {
        int q = v.front();
        v.pop(); vis[q] = 0;
        for (int i = 0; i < mp[q].size(); i++) {
            if (dis[mp[q][i].s1] > dis[q] + mp[q][i].side) {
                dis[mp[q][i].s1] = dis[q] + mp[q][i].side;//更新最短路径。
                if (vis[mp[q][i].s1]) {
                    continue;//如果已经标记，则继续下一次循环
                }
                v.push(mp[q][i].s1);
            }

        }
    }
}
int main()
{
    int x, y, r;

    cin >> n >> m >> s;
    init();
    while (m--) {
        node h;
        cin >> x >> y >> r;
        h.s1 = y;//因为该图为有向图，记录指向的结点
        h.side = r;//记录路径
        mp[x].push_back(h);
    }
    Spfa(s);
    for (int i = 1; i <= n; i++) {        
            cout << dis[i] << " ";
    }
}