剑指 Offer 51. 数组中的逆序对
题目说明
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
解题思路1:暴力
肯定是可行但是会超时的,就不用考虑了,但理论可行
解题思路2:归并
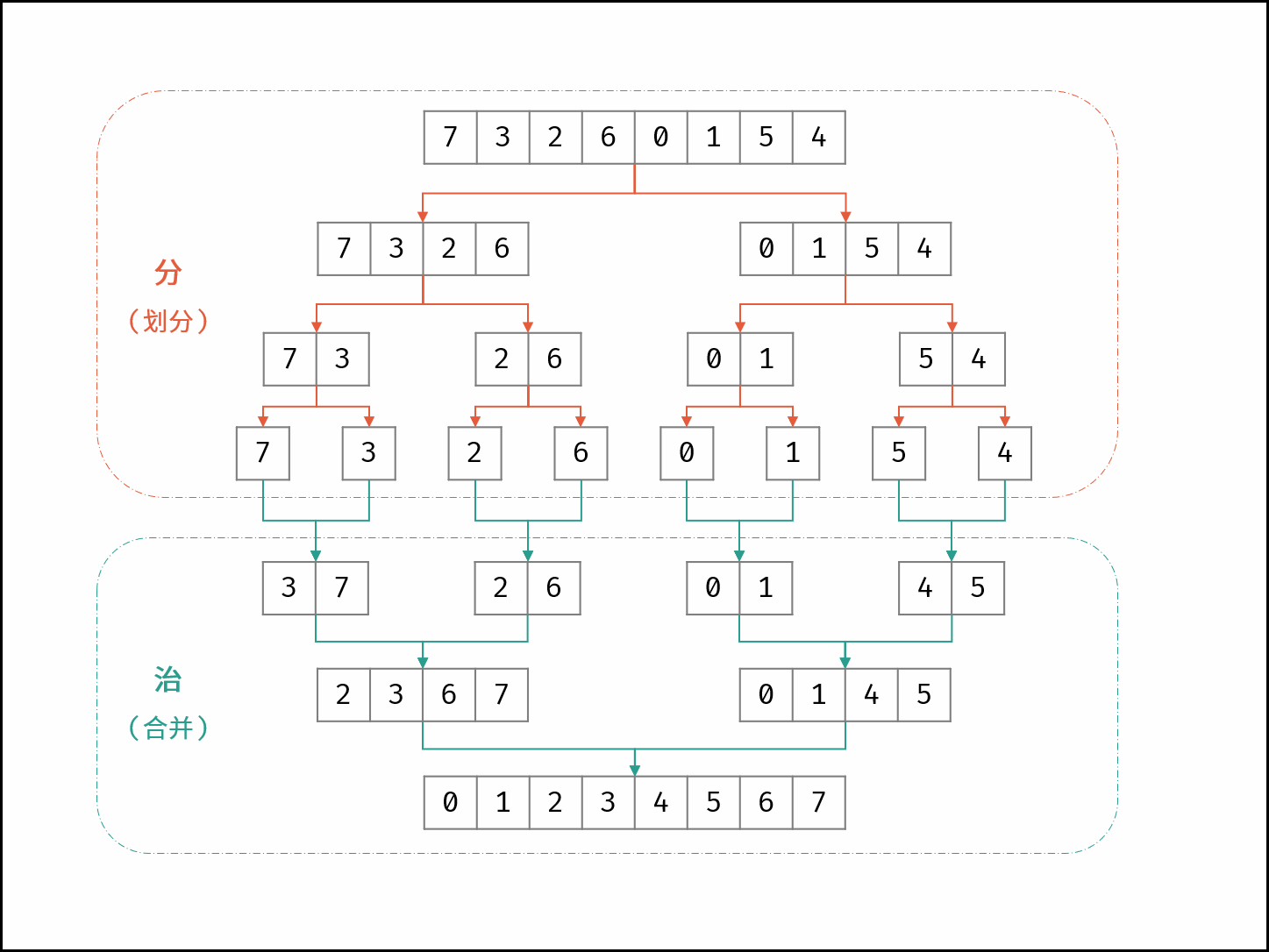
可以利用归并排序时的一个特性。当我们在并的阶段时,我们需要对左半边和右半边数组进行比较并且生成一个新的从小到大排序的数组。而我们在进行比较的时候,其实就相当于进行了逆序的判断:如果右半边数组比左半边小的话,则右边先进数组,说明这是一个逆序。我们可以计入逆序对总数count,要注意的是,当判定到此时left[i] > right[j]时,left后续的元素也是大于right[j]的,所以count += left.length - i
剑指 Offer 45. 把数组排成最小的数
题目说明
输入一个非负整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。输出结果可能非常大,所以你需要返回一个字符串而不是整数
解题思路
其实同样也是一个排序,只是排序的方式变了。在这道题中,判定哪个数字小(或者说位置应该排在前面)比较的不是数字的大小也不是字符串的大小(因为“3”比“30”小但是应该“30”排在前面),因此这里用到了一个关键的比较逻辑:(a + b).compareTo(b + a),仍然以前面的“3”和“30”为例,“303”是小于“330”,在这个逻辑中可以得到体现。因此我们依照此逻辑写一个排序即可,本题使用了快排
复习一下快排。快排的核心思想是为设置好的数字(我设置为最左边的数字)找到合适的位置,升序排序的话则要保证该位置左边的数字都小于等于它而右边的数字都大于等于它,然后我们就可以对左右两边分别进行快排直到子数组中只有一个元素为止
在这道题中也是一样的道理,只是修改了比较大小的逻辑
while (true) {
while (i < j && (strArray[j] + strArray[left]).compareTo(strArray[left] + strArray[j]) >= 0) {
j--;
}
while (i < j && (strArray[i] + strArray[left]).compareTo(strArray[left] + strArray[i]) <= 0) {
i++;
}
if (i >= j) {
break;
}
tmp = strArray[i];
strArray[i] = strArray[j];
strArray[j] = tmp;
}
tmp = strArray[left];
strArray[left] = strArray[i];
strArray[i] = tmp;
大顶堆小顶堆
是基于完全二叉树进行构建的
然后交换0和9(头和末尾),输出9。循环直到没有数组中没有元素为止。不用真的去构建一棵树,利用完全二叉树的性质
// 返回当前节点的父节点
private int parent(int pos) { return (pos - 1) / 2; }
// 返回当前节点的左子节点
private int leftChild(int pos) { return (2 * pos) + 1; }
// 返回当前节点的右子节点
private int rightChild(int pos) { return (2 * pos) + 2; }