【题解】Luogu[P7706] 「Wdsr-2.7」文文的摄影布置

Link

一道很有意思的线段树题。

第一步分析，我们要求最大的 \(a_i+a_k-\min{(b_j)}\)，事实上我们可以直接省去这个 \(\min\) 因为要最大化这个东西，选出来的 \(b_j\) 必然是最小的，所以原题转化为给定 \(l,r\) 求 \(\max{(a_i-b_j+a_k)}\) 其中 \(i<j<k\)。

第二步分析，我们发现这是一个单点修改、区间查询的问题，遇到这种问题一般都从区间合并入手，我们考虑怎么合并两个区间。

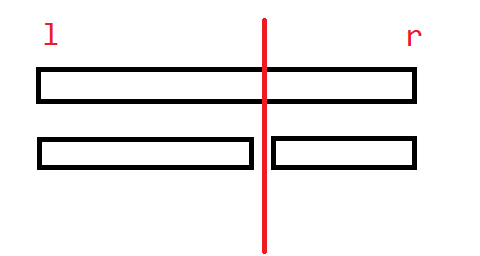
将左右两个区间合并成上面一个大区间，我们有四种情况：

1. \(i,j,k\) 均在左区间，那么答案即为左区间答案。
2. \(i,j,k\) 均在右区间，那么答案即为右区间答案。
3. \(i,j\) 在左区间，\(k\) 在右区间，那么答案即为左区间中最大的 \(a_i-b_j\ (i<j)\) 加上右区间中最大的 \(a_k\)。
   
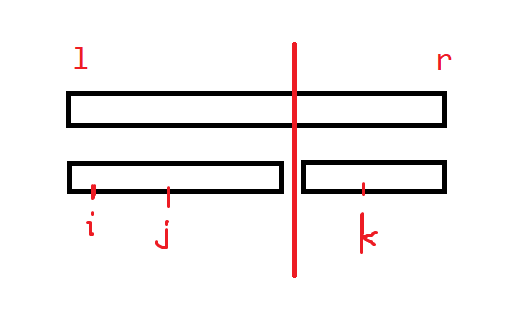
4. \(i\) 在左区间，\(j,k\) 在右区间，那么答案即为左区间中最大的 \(a_i\) 加上右区间中最大的 \(-b_j+a_k\ (j<k)\)。
   

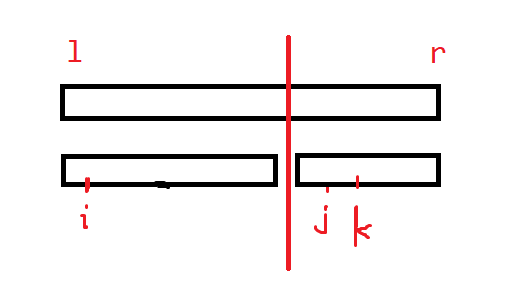
发现我们很好用线段树维护 1、2 种情况和 3 的右区间和 4 的左区间。

第三步分析，我们需要维护 3 情况的左区间和 4 情况的右区间。

以 3 情况左区间为例，我们同样分成两个小区间，看如何合并：

1. \(i,j\) 均在左区间，那么答案即为左区间答案。
2. \(i,j\) 均在右区间，那么答案即为右区间答案。
3. \(i\) 在左区间 \(j\) 在右区间，那么答案即为左区间中最大的 \(a_i\) 减去右区间中最小的 \(b_j\)。
   

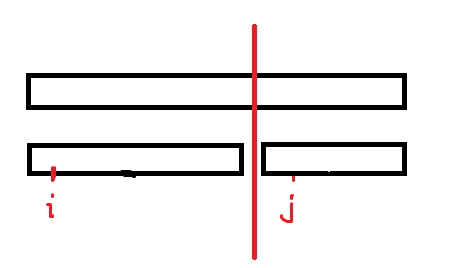
4 情况的右区间同理。

于是我们发现，我们很容易就能用线段树维护区间中的最大 \(a_i\) 与区间中最小的 \(b_j\) 了。

于是这道题的各种信息就很好的用线段树维护了。

code

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define ls(P) (P<<1)
#define rs(P) (P<<1|1)
const int inf=1e9,NR=5e5+5,SZ=4*NR;
int n,m;
int a[NR],b[NR];
struct node{
    int mxa,mnb,ij,jk,w;
    node():mxa(-inf),mnb(inf),ij(-inf),jk(-inf),w(-inf){}
}tree[SZ];
node operator +(node l,node r){
    node res;
    res.mxa=max(l.mxa,r.mxa),res.mnb=min(l.mnb,r.mnb);
    res.ij=max(max(l.ij,r.ij),l.mxa-r.mnb),res.jk=max(max(l.jk,r.jk),r.mxa-l.mnb);
    res.w=max(max(l.w,r.w),max(l.ij+r.mxa,l.mxa+r.jk));
    return res;
}
void bld(int l,int r,int p){
    if(l==r){tree[p].mxa=a[l],tree[p].mnb=b[l];return;}
    int mid=l+r>>1;
    bld(l,mid,ls(p)),bld(mid+1,r,rs(p));
    tree[p]=tree[ls(p)]+tree[rs(p)];
}
void mfy(int l,int r,int x,int p){
    if(l==r){tree[p].mxa=a[l],tree[p].mnb=b[l];return;}
    int mid=l+r>>1;
    if(x<=mid)mfy(l,mid,x,ls(p));
    else mfy(mid+1,r,x,rs(p));
    tree[p]=tree[ls(p)]+tree[rs(p)];
}
void qry(int l,int r,int s,int t,int p,node &num){
    if(s<=l&&r<=t){num=num+tree[p];return;}
    int mid=l+r>>1;
    if(s<=mid)qry(l,mid,s,t,ls(p),num);
    if(t>mid)qry(mid+1,r,s,t,rs(p),num);
}
signed main(){
    cin>>n>>m;
    for(int i=1;i<=n;++i)cin>>a[i];
    for(int i=1;i<=n;++i)cin>>b[i]; 
    bld(1,n,1);
    for(int i=1;i<=m;++i){
        int op,x,y;cin>>op>>x>>y;
        node res;
        if(op==1)a[x]=y,mfy(1,n,x,1);
        if(op==2)b[x]=y,mfy(1,n,x,1);
        if(op==3)qry(1,n,x,y,1,res),cout<<res.w<<endl;
    }
    return 0;
}