标签：元素 hash 次数 Cache 访问 Probation TinyLru

一、LRU

每次淘汰最久未访问的那个元素

可以用双向链表 + hash实现

主要流程

插入

直接插入到队头

查找

通过hash找到对应元素，然后将这个元素调整到队头

淘汰

队尾元素就是最久未访问的那个元素，直接淘汰

实现

GitHub

存在的问题

最明显的，LRU淘汰的是最久未访问的元素，比如队列大小为3，访问如下

a a a a b c d

执行到d时，a就会被淘汰，访问频率最高的元素被删除，显然这是有一些不合理的，所以如果要改进这个算法，我们希望的是能够记录每个元素的访问次数信息，每次淘汰访问次数最少的那个。

所以就有了LFU，

二、LFU

LFU需要记录每条数据的访问次数信息，每次淘汰访问次数最少的那条数据

\(O(\log_2^N)\)复杂度实现

用小根堆 + hash实现

插入

插入元素到小根堆的队尾和hash中，向上调整小根堆，时间复杂度\(O(\log_2^N)\)

查找

通过hash找到元素，增加访问次数，访问次数增加，向下调整小根堆，时间复杂度\(O(\log_2^N)\)

淘汰

1. 删除hash中的值

2. 小根堆顶就是访问次数最小的元素，按照堆调整的逻辑，将最后一个元素放置到堆顶，然后执行一次向下调整，时间复杂度\(O(\log_2^N)\)

实现

GitHub

O(1)复杂度实现

论文地址http://dhruvbird.com/lfu.pdf

用双向链表+hash实现

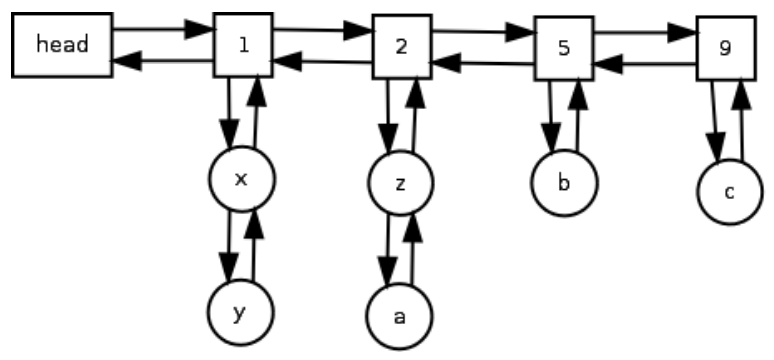
相同访问频率在一个子节点中，每个访问频率占据一个子节点

三、存在的问题

LRU存在的问题

• LRU 不抗扫描。这意味着，给定 N 个项目，攻击者可以按顺序发送 N+1 个请求。一旦初始扫描完成，所有后续扫描都将导致缓存未命中。
• 每次访问都需要移动队列中的对象。这会导致高速缓存未命中开销、TLB 颠簸和内存写入。

LFU存在的问题

1. 老数据影响命中率：某个数据项在之前被大量访问，导致其访问次数很高。之后很少访问，但是因为之前累积的高访问次数，导致长期无法被淘汰，影响命中率
2. 内存消耗问题：需要维护每个数据项的访问频率，这可能占用较大的内存空间，尤其是在大型缓存中。
3. 难以应对突发的稀疏流量：稀疏流量只有很少的访问量，在比较访问频率来决定去还是留时处于劣势，会导致稀疏流量缓存项频繁被淘汰。

四、TinyLFU

4.1 Count-Min Sketch

为解决第1、2问题，可采用CMS算法

加速查找

CMS和布隆过滤器类似，不过CMS在插入时，每个hash值对应的不是一个bit，而是多个bit，用于记录访问次数，查找时根据hash找出所有值，取最小值作为结果

减少内存消耗

每个存储访问频率的节点大小为4bit，所以访问次数最高为15，之后就停止增长(计数器只有4bit，所以被称为TinyLFU)

减少历史数据的影响

初始化时，存在一个阈值，一般是最大缓存项数的10倍，当访问次数达到访问阈值时，CMS内所有计数器值减半，访问次数也要调整，这样就可以解决大流量短时间内无法有效消除的问题

4.2 W-TinyLFU

接下来的Window Cache，解决了第3个问题，结构如下

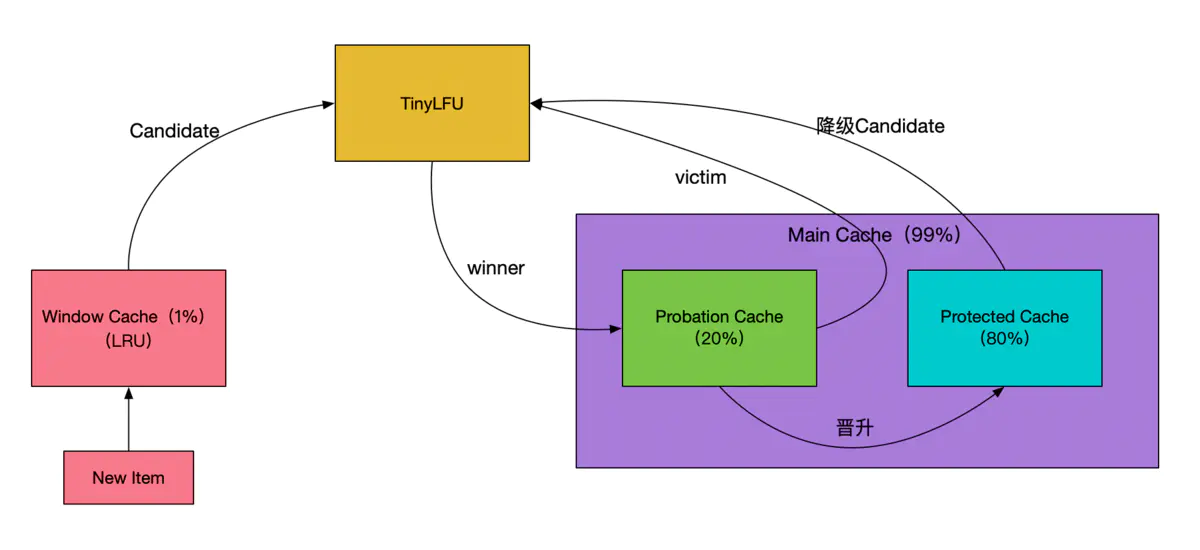
1. W-TinyLFU将缓存空间分为两大区域：Window Cache和Main Cache。
2. Main Cache由两个Cache组成：Protected Cache(受保护区域)和Probation Cache(观察区域)
3. Window, Protected, Probation，三个区域都是LRU
4. window Cache 默认为总缓存大小的 1%，Protected Cache占主缓存的20%，Probation Cache占主缓存的 80%。

规则

向外提供两个方法，Set和Get

Set流程

新数据到来，创建一个Node，先放入Windows Cache，此时分为两种情况

1. Window Cache没有满：直接返回
2. Window Cache已满：取出window的末尾元素，将其放入Probation
   1. 如果Probation没满，那就直接返回
   2. 如果Probation满了，取出Probation的末尾元素，然后和Window来的元素进行比较，根据cms确定的访问频率决定淘汰谁

Get流程

获取Node

1. 如果Node在window中，那就增加一次访问次数，然后移动到队头，返回。
2. 如果Node在Probation中，那就将节点移动到Protected，如果Protected已满，就淘汰末尾元素到Probation中
3. 如果Node在Protected中，那就增加一次访问次数，然后移动到队头，返回。

4.3 实现

Github

Reference

1. TinyLFU: A Highly Efficient Cache Admission Policy
2. Introduction to caffeine caching core principles
3. Caffeine源码解读-缓存过期淘汰相关算法
4. Design Of A Modern Cache

标签：元素,hash,次数,Cache,访问,Probation,TinyLru
From： https://www.cnblogs.com/INnoVationv2/p/17664761.html