圆方树板子题,这题真的有3000吗。
首先想到的是缩边双,但是以下情况边双不好处理:
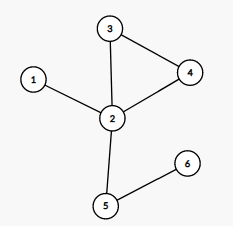
点 \(2,3,4\) 在一个边双里,缩点之后该边双在 \(1\) 到 \(6\) 的路径上,但是显然 \((2,3),(3,4),(2,4)\) 这三条边并不属于 \(1\) 到 \(6\) 的路径。
考虑建立圆方树,定义方点的权值为它所代表的边双中边的数量(只有一条边时权值为 \(0\)),那么答案就是圆方树上两点间方点权值和,正确性是显然的,因为如果方点在 \(a,b\) 两点间,那么 \(a\) 到 \(b\) 的路径一定会经过这个点双,点双里的边是随便删的。
建出圆方树,维护树上前缀和,倍增或者剖求 LCA 即可,离线可以做到 \(\mathcal O(n)\),不过数据范围 \(\mathcal O(n \log n)\) 即可通过。
int n,m,num,kl,cnt,x[600001],dfn[600001],y[600001],low[600001],sum[600001],top[600001],siz[600001],son[600001],dep[600001],fa[600001];
vector<int> T[600001],G[600001];
stack<int> st;
void tarjan(int k)
{
st.push(k),low[k]=dfn[k]=++cnt;
for(auto to:G[k])
{
if(!dfn[to])
{
tarjan(to),low[k]=min(low[k],low[to]);
if(low[to]>=dfn[k])
{
int y;++num;
do T[num].eb(y=st.top()),st.pop(),T[y].eb(num);while(y!=to);
T[num].eb(k),T[k].eb(num);
}
}
else low[k]=min(low[k],dfn[to]);
}
}
void dfs1(int k,int father,int depth)
{
dep[k]=depth,fa[k]=father,siz[k]=1;
for(auto to:T[k])
{
if(to==father)continue;
dfs1(to,k,depth+1),siz[k]+=siz[to];
if(siz[to]>siz[son[k]])son[k]=to;
}
}
void dfs2(int k,int topp)
{
if(sum[k]==1)--sum[k];
sum[k]+=sum[fa[k]],top[k]=topp;
if(son[k])dfs2(son[k],topp);
for(auto to:T[k])if(to!=fa[k]&&to!=son[k])dfs2(to,to);
}
inline int LCA(int x,int y)
{
while(top[x]!=top[y]){if(dep[top[x]]>dep[top[y]])swap(x,y);y=fa[top[y]];}
return dep[x]>dep[y]?y:x;
}
inline void mian()
{
read(n,m),num=n;int a,b;
for(int i=1;i<=m;++i)read(x[i],y[i]),G[x[i]].eb(y[i]),G[y[i]].eb(x[i]);
for(int i=1;i<=n;++i)if(!dfn[i])tarjan(i);
dfs1(1,0,1);
for(int i=1;i<=m;++i)
{
if(fa[x[i]]==fa[y[i]])++sum[fa[x[i]]];
else if(fa[fa[x[i]]]==y[i])++sum[fa[x[i]]];
else if(fa[fa[y[i]]]==x[i])++sum[fa[y[i]]];
}
dfs2(1,1),read(m);
while(m--)read(a,b),kl=LCA(a,b),write(sum[a]+sum[b]-sum[kl]-sum[fa[kl]],'\n');
}