后缀数组小结
借用了一下别人的 \(\rm blog\)。
简介
介绍一下基本数组。
我们把原串 \(\rm A\) 的所有后缀按字典序从小到大排个序,
则排名为 \(\rm i\) 的字符串是以第 \(\rm sa_i\) 个字符为起点的,且以第 \(\rm i\) 个字符为起点的后缀的排名是 \(\rm rk_i\)。
所以有 \(\rm sa_{rk_i}=i\)。
得到 \(\rm sa,rk\) 的方法是基数排序 + 倍增。
基数排序的思想就是按从低位到高位将数排序,可以做到 \(\rm O(n)\)。
解释一下代码:
假设原串是这样的:
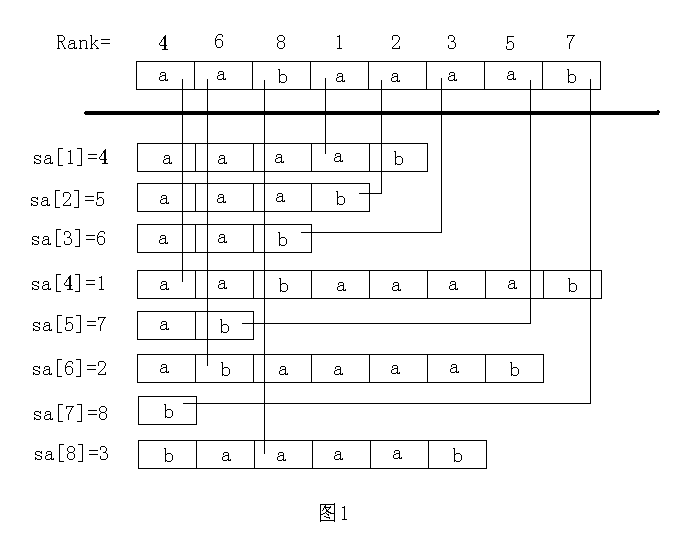
m=122;
for(int i=1;i<=n;++i) ++cnt[x[i]=A[i]];
for(int i=2;i<=m;++i) cnt[i]+=cnt[i-1];
for(int i=n;i;--i) sa[cnt[x[i]]--]=i;
这里 \(\rm cnt\) 是一个桶,用来记录每个字符出现的次数,\(\rm m\) 表示桶中数最大值是多少 (因为只有大小写英文字母或数字所以只需要 \(\rm 122\))。
这个代码也很好理解,就是对单个字符 (第一关键字)的排序。
排完序后 \(\rm sa\) 数组长这样:

for(int k=1;k<=n;k*=2){
这表示倍增。
int t=0;
for(int i=n-k+1;i<=n;++i) y[++t]=i;
for(int i=1;i<=n;++i)
if(sa[i]>k) y[++t]=sa[i]-k;
这表示对第二关键字的排序。
for(int i=1;i<=m;++i) cnt[i]=0;
for(int i=1;i<=n;++i) ++cnt[x[i]];
for(int i=2;i<=m;++i) cnt[i]+=cnt[i-1];
for(int i=n;i;--i) sa[cnt[x[y[i]]]--]=y[i],y[i]=0;
这里就直接结合两关键字的排序搞出了一个总排序。
\(\rm x\) 里面存了上次关键字的排序,在本次排序中即是第一关键字的排序,\(\rm x\) 的值排序等于第一关键字排序,这里的计数排序做的是对的。那么第二关键字呢?
前面对第二关键字进行了排序,在这里 \(\rm x_{y_i}\) 就是根据第二关键字的顺序重新改变了第一关键字的顺序,也就是说在本次计数排序中,出现先后次序排序等于第二关键字大小排序。
换句话说,我们先单独对第二关键字排序,根据这个顺序改变第一关键字的顺序,由于在计数排序时首先按照第一关键字的值排序,而第一关键字的值没有改变所以首先还是根据第一关键字排序,改变的是第一关键字相同的时候,出现在前面的第二关键字排在前面。
然后 \(\rm sa\) 长这样:

swap(x,y);
x[sa[1]]=1,t=1;
for(int i=2;i<=n;++i)
x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?t:++t;
if(t==n) break;
m=t;
这里我们就重新搞好了数组,可以继续倍增搞。
完整过程图片如下:

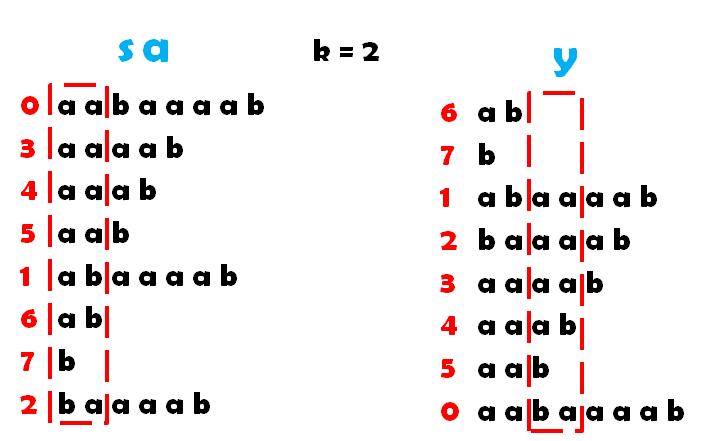
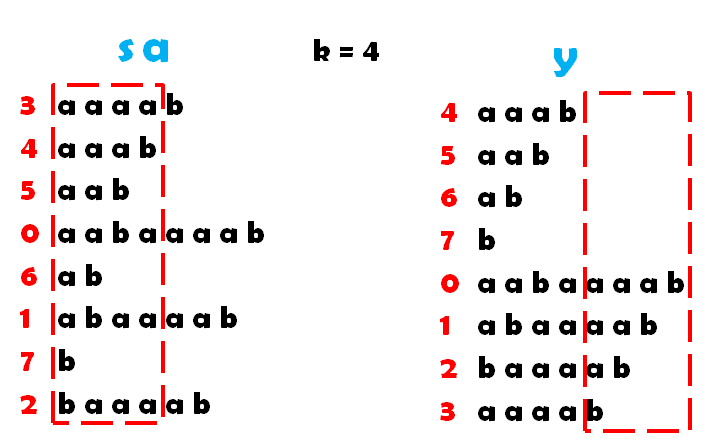

完整代码如下:
inline void get_sa(){
m=122;
for(int i=1;i<=n;++i) ++cnt[x[i]=A[i]];
for(int i=2;i<=m;++i) cnt[i]+=cnt[i-1];
for(int i=n;i;--i) sa[cnt[x[i]]--]=i;
for(int k=1;k<=n;k*=2){
int t=0;
for(int i=n-k+1;i<=n;++i) y[++t]=i;
for(int i=1;i<=n;++i)
if(sa[i]>k)
y[++t]=sa[i]-k;
for(int i=1;i<=m;++i) cnt[i]=0;
for(int i=1;i<=n;++i) ++cnt[x[i]];
for(int i=2;i<=m;++i) cnt[i]+=cnt[i-1];
for(int i=n;i;--i) sa[cnt[x[y[i]]]--]=y[i],y[i]=0;
swap(x,y);
x[sa[1]]=1,t=1;
for(int i=2;i<=n;++i)
x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?t:++t;
if(t==n) break;
m=t;
}
}