CF1144G:
给定一个长度为 \(n\) 的序列 \(A\)。
问能否把它拆成一个严格递增序列和一个严格递减序列(可以为空),如果有解则输出方案。
\(n\le 2\times 10^5\)。
设 \(f_{i,0}\) 表示把序列的前 \(i\) 个数拆成递增序列和一个递减序列(可以为空),并且 \(A_i\) 属于递增序列时,递减序列结尾可能的最大值。\(f_{i,1}\) 表示 \(A_i\) 属于递减序列时,递增序列结尾可能的最小值。
转移有四种:
- \(A_{i-1},A_i\) 都属于递增序列,则若 \(A_{i-1}\lt A_i\),则用 \(f_{i-1,0}\) 更新 \(f_{i,0}\)。
- \(A_{i-1},A_i\) 都属于递增序列,情况类似。
- \(A_{i-1}\) 属于递减序列,\(A_i\) 属于递增序列,则若 \(f_{i-1,1}\lt A_i\),用 \(A_{i-1}\) 更新 \(f_{i,0}\)。
- \(A_{i-1}\) 属于递增序列,\(A_i\) 属于递减序列,情况类似。
为了输出方案,记 \(g_{i,0}\) 表示在最优方案中,\(A_{i-1}\) 属于哪个序列,\(g_{i,1}\) 同理。
实现时可以把 \(f,g\) 用 pair<int,int> 压在一起。
Code:
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
typedef pair <int, int> pii;
const int N = 200005, inf = 0x3f3f3f3f;
int n;
int a[N];
int ans[N];
pii f[N][2];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
f[1][0].fi = inf, f[1][1].fi = -1;
for (int i = 2; i <= n; ++i) {
f[i][0].fi = -1, f[i][1].fi = inf;
if (a[i - 1] < a[i]) f[i][0] = pii(f[i - 1][0].fi, 0);
if (a[i - 1] > a[i]) f[i][1] = pii(f[i - 1][1].fi, 1);
if (f[i - 1][1].fi < a[i]) f[i][0] = max(f[i][0], pii(a[i - 1], 1));
if (f[i - 1][0].fi > a[i]) f[i][1] = min(f[i][1], pii(a[i - 1], 0));
}
if (~f[n][0].fi || f[n][1].fi < inf) {
printf("YES\n");
ans[n] = ~f[n][0].fi ? 0 : 1;
for (int i = n; i > 1; --i) ans[i - 1] = f[i][ans[i]].se;
for (int i = 1; i <= n; ++i) printf("%d ", ans[i]);
}
else printf("NO");
return 0;
}
CF1693D:
给出一个排列,求出这个排列中有多少个子区间,满足能够被划分为一个严格递增序列和一个严格递减序列(可以为空)。
很神奇的性质题啊
首先状态沿用上面一题的
首先有个很暴力的想法,从小到大枚举左端点,尝试扩展右端点,这样做是 \(\mathcal O(n^2)\) 的。
换种思路,我们从大到小枚举左端点。
考虑在 DP 过程中,如果一个点的 DP 值均没变,那么直接继承上一个位置能扩展到的最远点。否则如果拆不下去了,就更新最远点。
这看起来是个常数优化,但是这把 \(\mathcal O(n^2)\) 降到了 \(\mathcal O(n)\) !!!神奇吧
证明:
在 \(i\) 之前找到最大的一个 \(j\),满足 \(A_j\gt A_{j+1}\),那么 \(A_j,A_{j+1}\) 显然不能同时在递增序列中,\(f_{i,0}\) 的取值必然为 \(A_j,A_{j+1},-\infty\) 之一,若不存在这样的 \(j\),则 \(f_{i,0}=\infty\)。
也就是说,\(f_{i,0}\) 的取值只有 \(4\) 种情况。同理 \(f_{i,1}\) 的取值也只有 \(4\) 种情况。
每次更新至少有一个值改变,至多 \(8\) 个取值,所以时间复杂度是 \(\mathcal O(n)\) 的。
Code:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 200005, inf = 0x3f3f3f3f;
int n;
int a[N], f[N][2];
int lst;
ll ans;
void work(int l) {
f[l][0] = inf, f[l][1] = -inf;
for (int i = l + 1; i <= n; ++i) {
int w0 = -inf, w1 = inf;
if (a[i] > a[i - 1]) w0 = max(w0, f[i - 1][0]);
if (a[i] > f[i - 1][1]) w0 = max(w0, a[i - 1]);
if (a[i] < a[i - 1]) w1 = min(w1, f[i - 1][1]);
if (a[i] < f[i - 1][0]) w1 = min(w1, a[i - 1]);
if (f[i][1] == w1 && f[i][0] == w0) break;
else f[i][1] = w1, f[i][0] = w0;
if (f[i][0] == -inf && f[i][1] == inf) { lst = i - 1; break; }
}
ans += lst - l + 1;
}
int main() {
scanf("%d", &n), lst = n;
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
for (int i = n; i; --i) work(i);
printf("%lld", ans);
return 0;
}
CF1647F:
现在给出一个序列,把它恰好分成两个子序列,使得每一个子序列都是单峰的。
求两个单峰子序列的峰的组合,有多少种情况。(保证给出的序列元素互不相同)
首先状态还是沿用上面的
发现必然有一个峰值是全局最大值(位置设为 \(x\)),所以最终答案小于 \(n\)。
我们约定另一个峰值在最大值之右(位置设为 \(y\))(之左的情况 reverse 序列再做一遍)。那我们要做的就是:
- 将 \([1,x]\) 分解成两个递增序列,让不包含 \(x\) 位置的序列右端值最小(贪心)。
- 将 \([y,n]\) 分解成两个递减序列,同上方贪心让序列左端值最小。
- 将 \([x,y]\) 分解成(一个递减、一个递增)两个序列,必须保证 \(a_x\) 在递减序列里,\(a_y\) 在递增序列里。
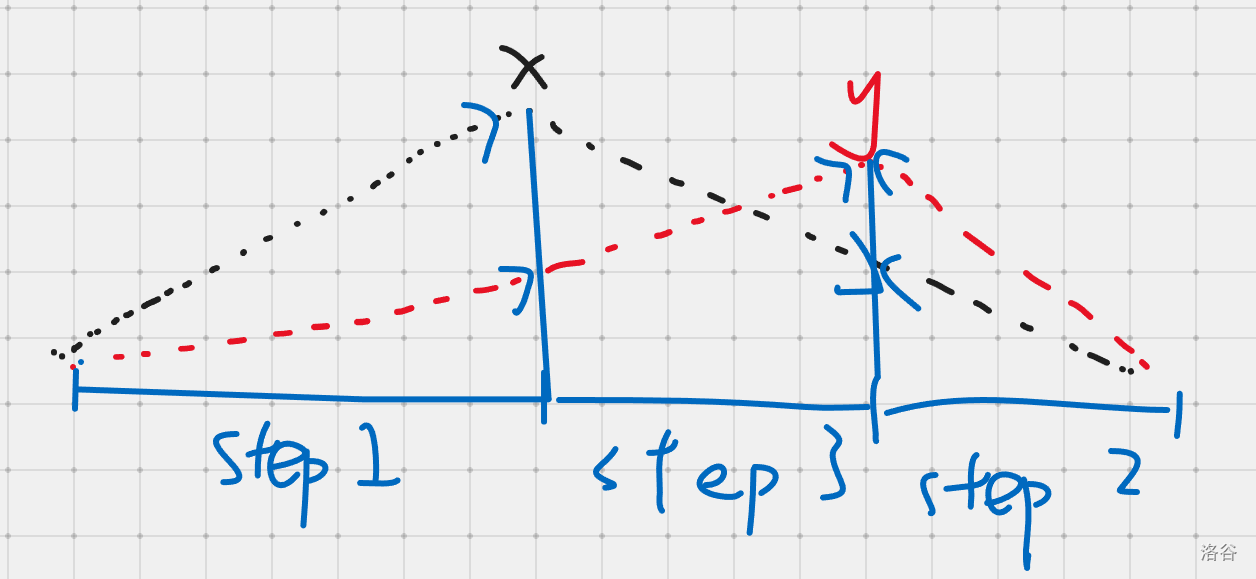
\(1,2\) 就用普通的线性 DP 解决,\(2\) 的 DP 数组要计算到 \(x+1\),DP 数组都要保存下来。
\(3\) 接上 \(1\) 的末尾,从 \(x\) 开始向右 DP,保存 DP 数组。
然后枚举 \(y\in[x+1,n]\),用 \(2,3\) 的 DP 数组判断能否接上,统计答案。
Code:
#include <bits/stdc++.h>
using namespace std;
const int N = 500005, inf = 0x3f3f3f3f;
int n, a[N];
int g[N], h[N], f[N][2];
int p;
int ans;
void chkmax(int &a, int b) { if (a < b) a = b; }
void chkmin(int &a, int b) { if (a > b) a = b; }
void solve() {
g[1] = 0;
for (int i = 2; i <= p; ++i) {
g[i] = inf;
if (a[i - 1] < a[i]) chkmin(g[i], g[i - 1]);
if (g[i - 1] < a[i]) chkmin(g[i], a[i - 1]);
}
if (g[p] == inf) return;
int val = g[p];
h[n] = 0;
for (int i = n - 1; i > p; --i) {
h[i] = inf;
if (a[i + 1] < a[i]) chkmin(h[i], h[i + 1]);
if (h[i + 1] < a[i]) chkmin(h[i], a[i + 1]);
}
f[p][0] = 0, f[p][1] = val;
for (int i = p + 1; i <= n; ++i) {
f[i][0] = 0, f[i][1] = inf;
if (a[i - 1] < a[i]) chkmax(f[i][0], f[i - 1][0]);
if (a[i - 1] > a[i]) chkmin(f[i][1], f[i - 1][1]);
if (f[i - 1][1] < a[i]) chkmax(f[i][0], a[i - 1]);
if (f[i - 1][0] > a[i]) chkmin(f[i][1], a[i - 1]);
}
for (int i = p + 1; i <= n; ++i) if (f[i][0] > h[i]) ++ans;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
for (int i = 1; i <= n; ++i) if (a[p] < a[i]) p = i;
solve();
p = n + 1 - p, reverse(a + 1, a + n + 1);
solve();
printf("%d", ans);
return 0;
}