普及模拟2
\(T1\) 地址 \(0pts\)
- 简化题意:判断一个 \(IP\) 地址是否合法(数据保证字符串中存在且仅存在4个被字符分开的整数)
#include<bits/stdc++.h> using namespace std; #define ll long long #define sort stable_sort #define endl '\n' char s[100]; int main() { freopen("ip.in","r",stdin); freopen("ip.out","w",stdout); int len,i,sum=0,x=0,num=0,flag=0; cin>>(s+1); len=strlen(s+1); s[len+1]='.';//赛时写成s[i+1]='.'了,挂了100pts len++; for(i=1;i<=len;i++) { if('0'<=s[i]&&s[i]<='9') { if(!('0'<=s[i-1]&&s[i-1]<='9')) { if('0'<=s[i+1]&&s[i+1]<='9') { if(s[i]=='0') { flag=1; break; } } } x=x*10+s[i]-'0'; } else { if(x>255||s[i]!='.') { flag=1; break; } if(s[i]=='.') { num++; } if(num>=4) { flag=1; break; } x=0; } } if(flag==0&&num==3) { cout<<"YES"<<endl; } else { x=flag=0; cout<<"NO"<<endl; for(i=1;i<=len;i++) { if('0'<=s[i]&&s[i]<='9') { x=x*10+s[i]-'0'; flag=1; } else { if(flag==1) { sum++; if(sum<=4) { cout<<min(x,255); } if(sum<=3) { cout<<"."; } if(sum==4) { break; } } x=flag=0; } } } return 0; }
\(T2\) 内积 \(100pts\)
- 简化题意:给定两个长度为 \(n(1 \le n \le 10^6)\) 的数组 \(a,b(-10^6 \le a_i,b_i \le 10^6)\) ,可以任意交换两个数组中元素的顺序,得到两个新的数组,求 \(\sum\limits_{i=1}^{n}=a_i b_i\) 的最大值。
- 考虑将数组 \(a,b\) 排序,此时的 \(\sum\limits_{i=1}^{n}=a_i b_i\) 即为所求。
- 前置知识:若 \(a_1<a_2,b_1<b_2\) ,有 \(a_1 b_1+a_2 b_2>a_1 b_2+a_2 b_1\) 。
- 证明:因为 \(a_1<a_2,b_1<b_2\) ,所以有 \(b_2-b_1>0,a_2-a_1>0\) ,故 \((a_2-a_1) (b_2-b_1)>0\) ,展开得 \(a_2 b_2-a_2 b_2-a_1 b_2+a_1 b_1>0\) ,移项得 \(a_1 b_1+a_2 b_2>a_1 b_2+a_2 b_1\) 。
#include<bits/stdc++.h> using namespace std; #define ll __int128_t //赛时怕炸long long就开了int128,但不开int128也能过 #define sort stable_sort #define endl '\n' ll read() { ll x=0,f=1; char c=getchar(); while(c>'9'||c<'0') { if(c=='-') { f=-1; } c=getchar(); } while('0'<=c&&c<='9') { x=x*10+c-'0'; c=getchar(); } return x*f; } void write(ll x) { if(x<0) { putchar('-'); x=-x; } if(x>9) { write(x/10); } putchar((x%10)+'0'); } ll a[2000001],b[2000001]; int main() { freopen("nj.in","r",stdin); freopen("nj.out","w",stdout); ll n,i,ans=0; n=read(); for(i=1;i<=n;i++) { a[i]=read(); } for(i=1;i<=n;i++) { b[i]=read(); } sort(a+1,a+1+n); sort(b+1,b+1+n); for(i=1;i<=n;i++) { ans+=a[i]*b[i]; } write(ans); return 0; } - 前置知识:若 \(a_1<a_2,b_1<b_2\) ,有 \(a_1 b_1+a_2 b_2>a_1 b_2+a_2 b_1\) 。
\(T3\) 翻转 \(10pts\)
\(T4\) 阶乘 \(40pts\)
-
简化题意: \(T\) 组询问,每组询问给出 \(n\) ,求出所有满足 \(n=\dfrac{a!}{b!}\) 的 \(a,b\) 及数量或给出无解信息(输出
-1)。 -
赛时乱搞的一个算法:预处理 \(1 \sim 30\) 的阶乘,然后枚举右端点一直到 \(30\) ,接着枚举左端点,骗到了 \(40pts\) 。
-
正解:
- \(n=1\) 时,输出
-1。 - \(n \in \mathbb{P}\) 时,仅存在一组答案 \(a=n,b=n-1\) 。
- 打表发现阶乘的增长速度极快,\(20! \approx 2 \times 10^{18}\) ,发现有 \(a-b \le 20\) ,枚举 \(d=a-b\) ,那么一定有 \(a^d \le n,b^d \ge n\) ,即 \(a \le \sqrt[d]{n},b \ge \sqrt[d]{n}\) 。
#include<bits/stdc++.h> using namespace std; #define ll long long #define sort stable_sort #define endl '\n' priority_queue<pair<ll,ll> >q; int main() { freopen("jc.in","r",stdin); freopen("jc.out","w",stdout); ll t,n,i,l,r,len,j,sum,ls; scanf("%lld",&t); for(i=1;i<=t;i++) { scanf("%lld",&n); if(n==1) { printf("-1\n"); } else { sum=0; for(len=2;len<=20;len++)//如果枚举到20不放心,可以再大一点 { for(r=pow(1.0*n,1.0/len);;r++) { l=r-len+1; if(l!=1)//特判l=1的时候 ,此时有b=0,但是除数不能为0 { ls=1; for(j=l;j<=r;j++)//直接枚举阶乘就行,也可以事先预处理出阶乘 { ls*=j; } if(ls>n) { break; } if(ls==n) { sum++; q.push(make_pair(-r,-(l-1))); break; } } } } sum++; q.push(make_pair(-n,-(n-1)));//因为枚举长度大于1,所以会漏掉a=n,b=n-1的情况 printf("%lld\n",sum); for(j=1;j<=sum;j++) { printf("%lld %lld\n",-q.top().first,-q.top().second); q.pop(); } } } return 0; } - \(n=1\) 时,输出
【LGR-155-Div.3】洛谷基础赛 #3 &「NnOI」Round 2
这场比赛和上午模拟赛讲评时间重了,打完 \(T1,T2\) 就溜了。

\(T1\) luogu P9569 Khronostasis Katharsis \(100pts\)
- 水题
#include<bits/stdc++.h> using namespace std; #define ll long long #define sort stable_sort #define endl '\n' int main() { ll n,m,i,v,t,ans=0,l=1;//l要初始化为1(当T=1时) cin>>n>>m; for(i=1;i<=n;i++) { cin>>v>>t; if((m-t)*v>ans) { ans=(m-t)*v; l=i; } } cout<<l; return 0; }
\(T2\) luogu P9570 Glaciaxion \(100pts\)
- 水题
#include<bits/stdc++.h> using namespace std; #define ll long long #define sort stable_sort #define endl '\n' char s[1000001]; int main() { int n,m,i,flag=0,sumn=0,l=0,r=0; char pd; cin>>n>>m>>(s+1); for(i=1;i<=m;i++) { if(s[i]=='N') { sumn++; } if(s[i]=='Y'&&sumn==0) { cout<<"No solution"<<endl; flag=1; break; } } if(flag==0) { if(sumn>n) { cout<<"No solution"<<endl; } else { for(i=1;i<=m;i++) { if(s[i]=='N') { l++; cout<<l<<" "; } if(s[i]=='Y') { cout<<"1 "; } } } } return 0; }
\(T3\) luogu P9571 Horizon Blue \(0pts\)
- 暂时咕了,有时间再打。
\(T4\) luogu P9572 Colorful Days♪ \(0pts\)
- 暂时咕了,有时间再打。
总结
- 上午模拟赛打到 \(8:50\) 就溜去打别的东西了,导致 \(T1\) 没有造出合理的 \(hack\) 数据,挂了 \(100pts\) 。
后记
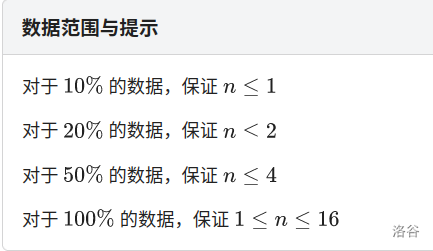
- \(T3\) 有 \(4\) 个数据范围。