二叉树
114. 二叉树展开为链表
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用
TreeNode,其中right子指针指向链表中下一个结点,而左子指针始终为null。 - 展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例 1:

输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [0]
输出:[0]
提示:
- 树中结点数在范围
[0, 2000]内 -100 <= Node.val <= 100
class Solution {
public:
//参返分析:输入根节点,无需返回值
//终止条件:根节点为空节点
//单层逻辑:获取链表化左子树,获取链表化右子树
//左子树置空,右子树拼接链表化左子树后再拼接链表化右子树,保证顺序为前序遍历的顺序
void func(TreeNode* root){
if(!root) return;
//链表化子树
func(root->left);
func(root->right);
//获取链表化子树
TreeNode* left = root->left;
TreeNode* right = root->right;
//左子树置空
root->left = nullptr;
//右子树拼接链表化左子树
root->right =left;
//右子树拼接链表化右子树
TreeNode* cur = root;
while(cur->right){
cur = cur->right;
}
cur->right = right;
}
void flatten(TreeNode* root) {
func(root);
}
};
105. 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
提示:
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorder和inorder均 无重复 元素inorder均出现在preorderpreorder保证 为二叉树的前序遍历序列inorder保证 为二叉树的中序遍历序列
图源自力扣
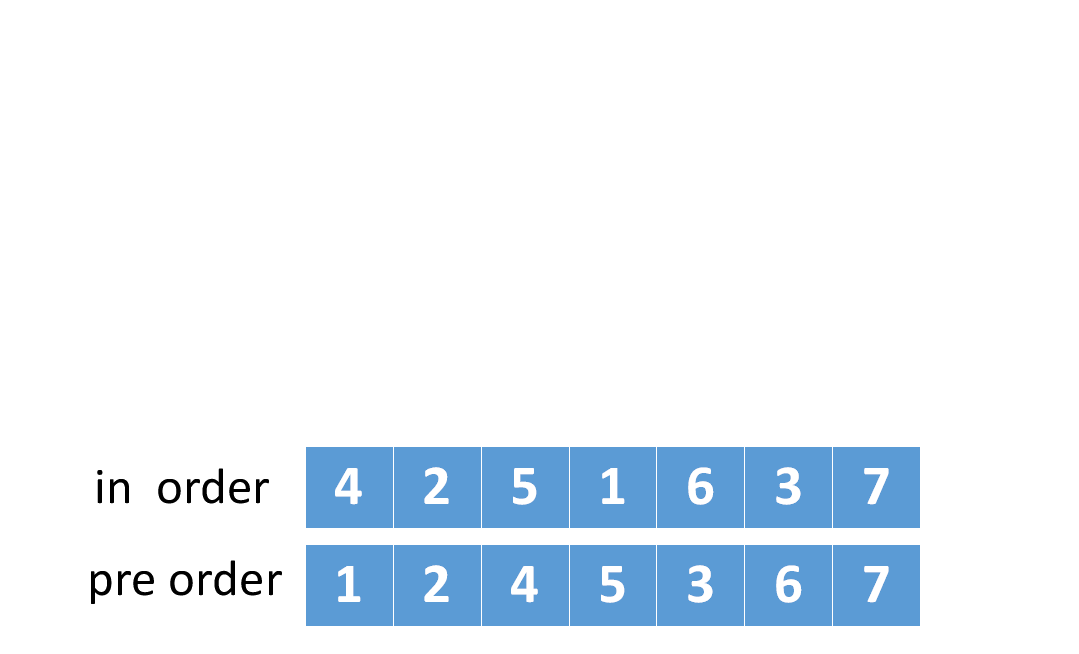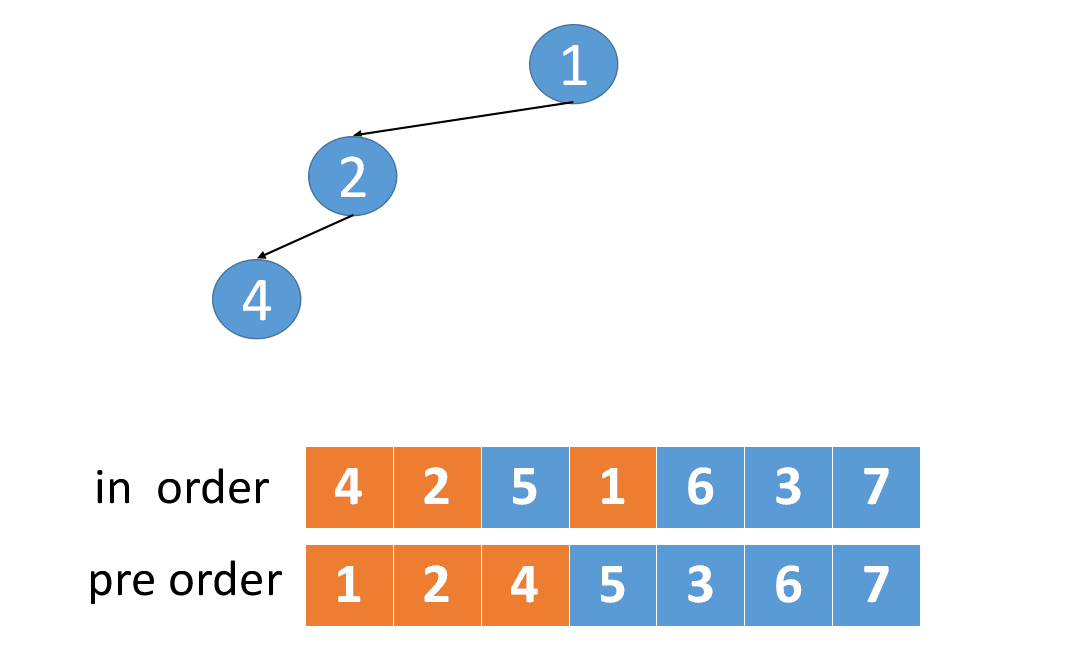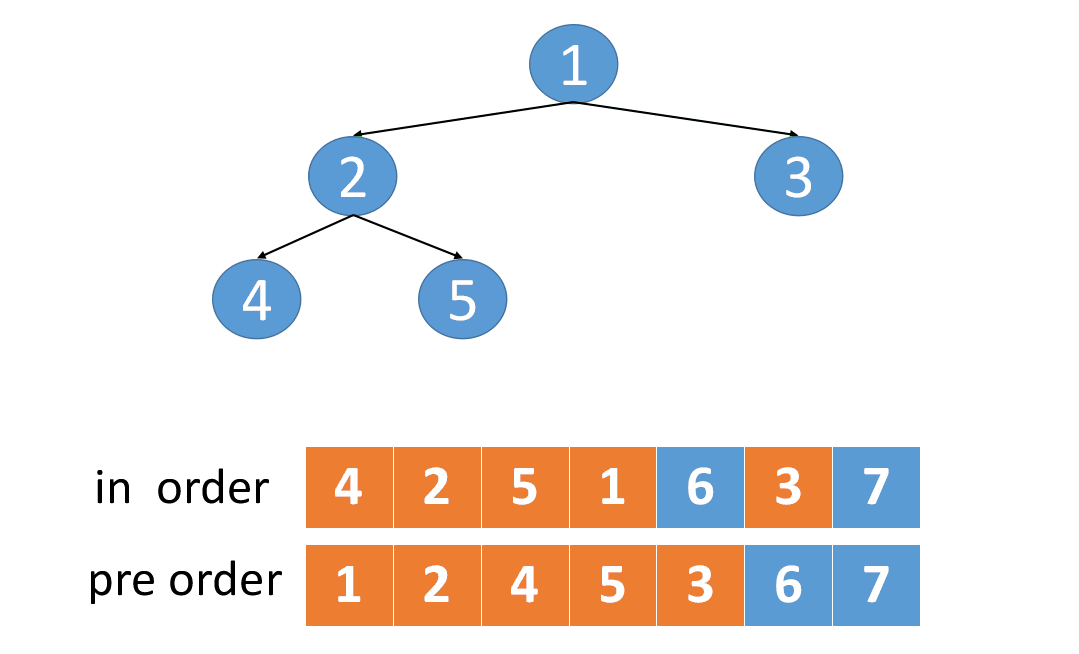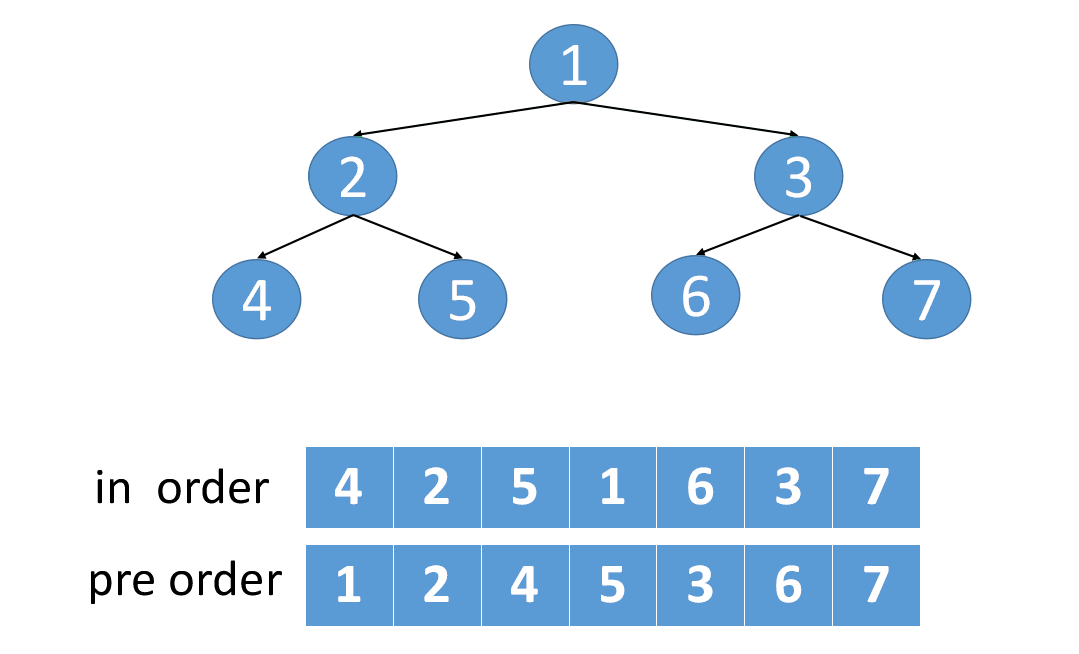
纯技巧,原子操作,记住就行
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if (preorder.empty() || inorder.empty()) {
return nullptr;
}
return buildTreeHelper(preorder, 0, preorder.size()-1, inorder, 0, inorder.size()-1);
}
//左闭右闭
TreeNode* buildTreeHelper(vector<int>& preorder, int preorderStart, int preorderEnd,
vector<int>& inorder, int inorderStart, int inorderEnd) {
//左闭右闭终止条件:start > end
if (preorderStart > preorderEnd || inorderStart > inorderEnd) {
return nullptr;
}
// 前序遍历的第一个节点是根节点,补全中序所丢失的信息
int rootVal = preorder[preorderStart];
TreeNode* root = new TreeNode(rootVal);
// 在中序遍历中找到根节点的位置
int rootPos;
for (int i = inorderStart; i <= inorderEnd; i++) {
if (inorder[i] == rootVal) {
rootPos = i;
break;
}
}
// 分割中序遍历序列为左子树和右子树部分
// 中序遍历:左子树 根节点 右子树,由此可得左子树节点数 和 右子树节点数,补全前序所缺失的信息
// 根节点下标为:rootPos,易得 leftSize 和 rightSize
int leftSize = rootPos - inorderStart;
int rightSize = inorderEnd - rootPos;
// 分割前序遍历序列为根节点、左子树和右子树三部分
// 前序遍历为:根节点 左子树 右子树
int preorderLeftEnd = preorderStart + leftSize;
int preorderRightStart = preorderEnd - rightSize + 1;
//right - len + 1 是一个表达式,其中 right 代表最右边的索引位置,len 代表列表的长度。这个表达式的结果是将列表中的元素排列在右边时,右边的起始索引位置。
//为什么要 + 1 呢?这是因为索引是从 0 开始计数的。所以,当计算右边的起始索引位置时,我们需要将列表的长度加上 1。这样,右边的范围将包括最右边的元素,进而保证了左闭右闭
// 处理左子树和右子树
// preStart 已经作为根节点处理
// 故前序被分为 [preStart + 1, preorderLeftEnd] [preorderRightStart, preorderEnd]
// rootPos 已经作为根节点处理
// 故中序被分为 [inorderStart, rootPos - 1] [rootPos + 1, inorderEnd]
root->left = buildTreeHelper(preorder, preorderStart + 1, preorderLeftEnd, inorder, inorderStart, rootPos - 1);
root->right = buildTreeHelper(preorder, preorderRightStart preorderEnd, inorder, rootPos + 1, inorderEnd);
return root;
}
};
437. 路径总和 III
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
示例 1:

输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出:3
解释:和等于 8 的路径有 3 条,如图所示。
示例 2:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:3
提示:
- 二叉树的节点个数的范围是
[0,1000] -109 <= Node.val <= 109-1000 <= targetSum <= 1000
class Solution {
public:
int count=0;
//参返分析:输入根节点、当前和 & 目标和
//终止条件:根节点为空,返回路径数为 0
//单层逻辑:如果加入当前节点后值为 target,证明找到了目标路径,count++
void dfs(TreeNode* root, long targetSum,long sum){
if(!root) return;
sum+=root->val;
if(sum==targetSum) count++;
dfs(root->left,targetSum,sum);
dfs(root->right,targetSum,sum);
}
int pathSum(TreeNode* root, long targetSum) {
if(!root) return 0;
//使用dfs来遍历二叉树,并计算从根节点到当前节点的路径之和。当我们遍历到某个节点时,我们检查当前路径之和是否等于目标和,如果是,则计数器加1。
dfs(root,targetSum,0);
//然而,当前节点到根节点的路径可能不止一条。我们需要通过再次调用pathSum函数来遍历当前节点的左子树和右子树,以计算所有可能的路径。这样,我们就能将路径不仅仅限制在根节点到当前节点上,而是可以从任意节点开始。
pathSum(root->left,targetSum);
pathSum(root->right,targetSum);
return count;
}
};
236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1
提示:
- 树中节点数目在范围
[2, 105]内。 -109 <= Node.val <= 109- 所有
Node.val互不相同。 p != qp和q均存在于给定的二叉树中。
class Solution {
public:
//参返分析:输入根节点,待查找公共祖先的节点 p、q,返回最近公共祖先
//终止条件:
//当根节点为空时,直接返回 nullptr,即返回 root
//当根节点非空时,若根节点为待查找公共祖先的任意节点,则最近公共祖先节点为节点本身,即返回 root
//单层逻辑:
//如果左子树和右子树分别包含p和q,则当前节点为最近公共祖先
//如果左(右)子树只包含p或q,则返回包含了节点p或q的子树
TreeNode* func(TreeNode* root, TreeNode* p, TreeNode* q){
// 如果当前节点为空或等于p或q,则返回该节点(归并)
if(!root || root == p || root == q){
return root;
}
// 递归查找左子树和右子树
TreeNode* left = func(root->left, p, q);
TreeNode* right = func(root->right, p, q);
// 如果左子树和右子树分别包含p和q,则当前节点为最近公共祖先
if (left != nullptr && right != nullptr) {
return root;
}
// 如果左子树只包含p或q,则返回包含了节点p或q的子树
if (left != nullptr) {
return left;
}
// 如果右子树只包含p或q,则返回包含了节点p或q的子树
if (right != nullptr) {
return right;
}
return nullptr;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
return func(root, p, q);
}
};
124. 二叉树中的最大路径和
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例 1:

输入:root = [1,2,3]
输出:6
解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
示例 2:

输入:root = [-10,9,20,null,null,15,7]
输出:42
解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
提示:
- 树中节点数目范围是
[1, 3 * 104] -1000 <= Node.val <= 1000
class Solution {
public:
int maxPath = INT_MIN;
int func(TreeNode* root) {
if (root == nullptr) return 0;
//获取左子树最大路径和
int leftMax = max(0, func(root->left));
//获取右子树最大路径和
int rightMax = max(0, func(root->right));
//获取最大路径和
int pathSum = root->val + leftMax + rightMax;
//更新最大路径和
maxPath = max(maxPath, pathSum);
//返回经过当前节点的最大路径和
return root->val + max(leftMax, rightMax);
}
int maxPathSum(TreeNode* root) {
func(root);
return maxPath;
}
};