- [1] [蓝桥杯 2013 省 A] 剪格子 洛谷P8601
题目描述
如图 \(1\) 所示,\(3\times 3\) 的格子中填写了一些整数。
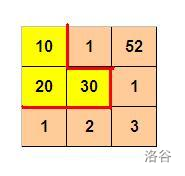
我们沿着图中的红色线剪开,得到两个部分,每个部分的数字和都是 \(60\)。
本题的要求就是请你编程判定:对给定的 \(m\times n\) 的格子中的整数,是否可以分割为两个部分,使得这两个区域的数字和相等。
如果存在多种解答,请输出包含左上角格子的那个区域包含的格子的最小数目。
如果无法分割,则输出 \(0\)。
输入格式
程序先读入两个整数 \(m\),\(n\) 用空格分割 \((m,n<10)\)
表示表格的宽度和高度。
接下来是 \(n\) 行,每行 \(m\) 个正整数,用空格分开。每个整数不大于 \(10000\)。
输出格式
程序输出:在所有解中,包含左上角的分割区可能包含的最小的格子数目。
样例 #1
样例输入 #1
3 3
10 1 52
20 30 1
1 2 3
样例输出 #1
3
样例 #2
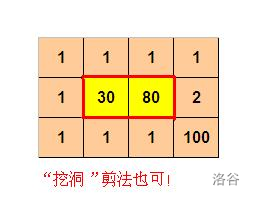
样例输入 #2
4 3
1 1 1 1
1 30 80 2
1 1 1 100
样例输出 #2
10
提示
第二个用例中:
时限 5 秒, 64M。蓝桥杯 2013 年第四届省赛
- [2] 题目分析:
First,既然分成两部分后使得两部分的和相等,那么存在两种特判情况,第一种是当所有的数加起来等于一个奇数时,肯定不满足题意,直接输出 0 ;
还有一种情况是当所有数中的最大数大于所有数和的一半时,例如一个 3 × 3 的矩阵:
1 1 1
10 1 1
1 1 1
矩阵当中的最大数是 10,而其余数加起来也才 8,显然不满足题意,So,还是输出 0 就行了。
Second,特判这两种情况后,开始搜索,我们从 a[1][1] 开始搜索,每次找上下左右四个方向最大的数,用 ans 来记录已经遍历过的数的和,再用一个 vis 数组记录当前位置已经走过,不能回头,然后当这个 ans 加 a[x][y] 超过了总和的一半时,说明不能往这边走,并且当 vis[x][y] 等于 1 时说明这里走过,不能走了。每走到一个点,用 cnt 记录走过点的数量,当 ans 等于总和的一半时,说明已经找到答案了,这时输出 cnt 的数量也就是遍历的最小的点的数量。
- [3] 代码实现:
#include<bits/stdc++.h>
using namespace std;
int a[15][15];
int n,m,res=0,cnt=0,ans=0,mx=0;
int dx[4]={1,-1,0,0};//方向数组
int dy[4]={0,0,1,-1};//方向数组
bool vis[15][15];// vis数组判断该点是否走过;
void dfs(int x,int y){
vis[x][y]=1;
cnt++;
ans+=a[x][y];
int maxn=0,maxi=0;
if(ans==res/2){//循环结束,输出cnt
printf("%d",cnt);
return ;
}
for(int i=0;i<4;i++){
if(x+dx[i]<1 || y+dy[i]<1 || x+dx[i]>n || y+dy[i]>m || vis[x+dx[i]][y+dy[i]]==1 || ans+a[x+dx[i]][y+dy[i]] > res/2) continue;
if(a[x+dx[i]][y+dy[i]]>maxn){
maxi=i;
maxn=a[x+dx[i]][y+dy[i]];//找最大的点进行遍历 和贪心思想差不多
}
}
if(x+dx[maxi]>0 && y+dy[maxi]>0 && x+dx[maxi]<=n && y+dy[maxi]<=m && vis[x+dx[maxi]][y+dy[maxi]]==0 && ans+a[x+dx[maxi]][y+dy[maxi]] <= res/2){//超出边界或已经找过或超过总和一半时退出
dfs(x+dx[maxi],y+dy[maxi]);
}
}
int main(){
scanf("%d%d",&m,&n);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
scanf("%d",&a[i][j]);
res+=a[i][j];
mx=max(mx,a[i][j]);
}
if(res%2!=0||mx>res/2){//特判两种情况
printf("0\n");
return 0;
}
dfs(1,1);//从左上角一开始遍历
return 0;
}
But,这一题有一个恶心的hack数据,会使深搜过不了,我也没办法,没事,反正其他点过了QWQ
