(笔记)信号完整性：差分信号——什么是差分对

一，什么是差分对

说到差分信号首先想到的是PCB或线缆上的差分对，这是差分信号的物理承载形式；那差分对是什么呢？从本质上来说仍然是传输线之间的相互关系，只是它相比于串扰更加特殊一点，更加有趣一点。

从定义来说差分对指的是：存在耦合的一对传输线。在差分对上承载的信号就是差分信令：用两个输出驱动器去驱动两条独立的传输线，一条线路传输1’b，而另外一条传输它的补；所测量到的信号是两条线之间的差，而这一差信号携带着传输信息。

差分信号相对于单端信号多了一条传输线，所以差分信号在传输过程中，同时也在传输单端信号。如之前章节对传输线的定义，单端信号是：驱动器在传输线上驱动一路信号时，在信号路径和返回路径之间存在的信号电压。而差分信号是：两路驱动器驱动一个差分对时，两路信号路径之间存在的信号电压差。

假设差分信号的两个单端信号电压分别是：V1和V2；那么接收端的差分接收器检测的是它们之间的信号电压差：Vdiff = V1-V2；同时电路上还存在共模信号：Vcomm = (V1+V2)/2。

那么差分信号相比于单端信号有哪些优点？

1. 差分信号幅度相对单端信号的摆幅更低，双驱动器产生的dI/dt比单端驱动器大幅降低，从而减小了地弹、轨道塌陷以及EMI干扰等问题；

2. 相比于单端放大器，接收器中的差分放大器有更高的增益；

3. 如果信号在一对紧耦合差分对中传播，对外串扰小且应对其它传输线的串扰较好；

4. 差分信号通过阻抗不连续点时，不易受到外部的干扰（抗共模干扰较强）；

5. 使用便宜的双绞线即可实现较远距离的差分信号的传输（5类线），成本较低。

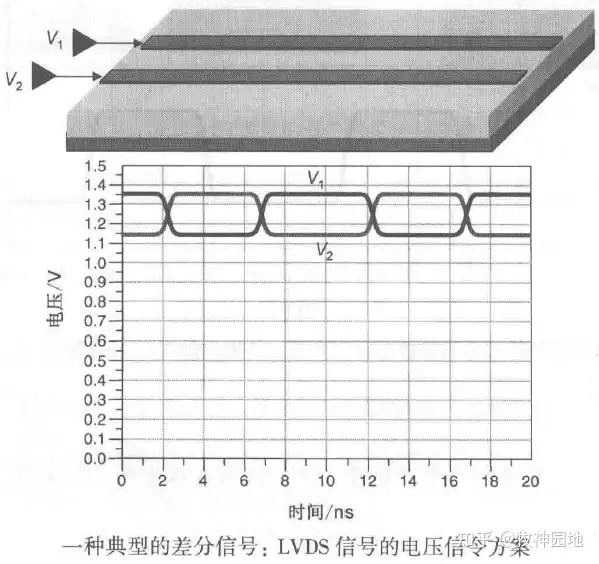
从理论上来说，任何两条传输线都可以构成一个差分对，每条传输线都可以是简单的单端传输线。

但这个定义感觉不靠谱啊，在实际应用中我们不会随意拿两条传输线就当作差分对来用的，而是会要求差分对：差分线等长、等宽，线间距保持一致，单端阻抗相等，等等。简而言之要求：差分对的两条传输线是一对保持对称姿势的双胞胎；因为任何的不对称都会导致差分信号的失真，并使部分差分信号转换成共模信号，而共模信号遇到不对称又会使部分共模信号转换成差分信号，造成差分信号质量的恶化。

1，差分阻抗

我们首先从阻抗的定义出发来定义差分阻抗：是差分信号感受到的阻抗，即，差分信号的电压与电流的比值。这是差分对最重要的电特性，它决定了差分信号的信号完整性。根据差分对之间的耦合关系，可以分成两种情况：

1，差分对之间无耦合；

2，差分对之间紧耦合。

接下来，我们根据这两种情况扩展开来分析。

1.1 无耦合

1. 假设差分对的两条传输线距离非常远（至少是线宽的2倍（3w原则））；每条信号线单端特征阻抗Z0=50ohm，流经信号线与返回路径之间的电流：Ione = Vone/Z0；

2. 沿着差分对传播的差分信号跳变就是两条信号线上的差，差分对之间的电压为每条信号线上跳变电压的2倍（Vdiff=2*Vone）；

3. 两条差分信号线上的电流大小相等、方向相反，所以我们可以将两条信号线看成一个电流回路：Ione电流从一条信号线流出，再流入另外一条信号线流回到源端；

4. 因此我们就可以计算出差分阻抗为：Zdiff = Vdiff/Ion = 2*Vone/Ione = 2*Z0；即差分阻抗是单端传输线阻抗的2倍。

5. 如下图所示，差分信号经差分对传输到了接收端，如果终端阻抗非常大（R开路），使得差分信号反射回源端，这种多次反射会产生振荡噪声；消除反射的方法是末端跨接一个端接电阻，匹配差分阻抗：Rterm = Zdiff = 2*Z0。

——当然，我们还可以将差分阻抗看成是两条传输线单端阻抗的串联，那么也可以单独将单端信号线做终端并联匹配Z0，此时差分线之间阻抗也是2*Z0。

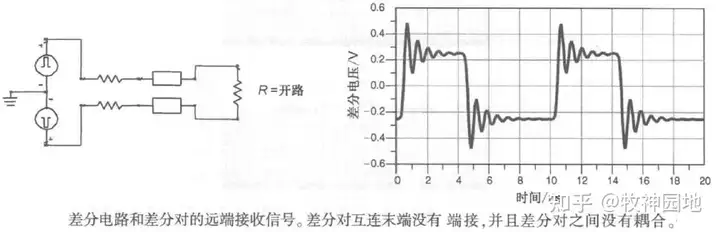
在实际设计中，无耦合差分线比我们想象中的应用场景还要多；因为芯片往往只定义了差分阻抗要求，如果差分阻抗要求为100ohm，那么设计成无耦合差分线会更加方便。只要做好参考平面以及边上传输线串扰的控制，无耦合差分线也是一个非常好的选择。

1.2 耦合

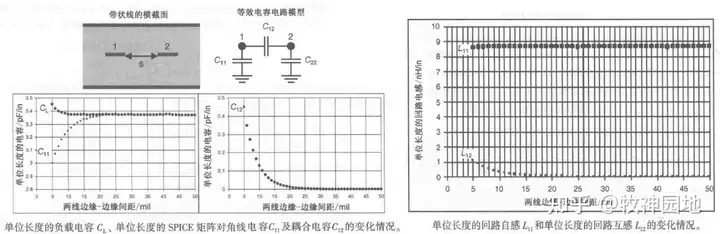
当差分对的两条信号线慢慢靠近，它们的边缘电场和磁场会相互覆盖，耦合程度会变的很强；此时差分阻抗的计算会变的复杂，我们在串扰章节中以互容C12和互感L12来描述两者的耦合强度，如下图所示为两条传输线之间距离与互容C12、互感L12之间的关系。

1. 如下左图所示，当信号线靠近时，C11和C12发生了改变，信号线1和回流路径之间的边缘场被邻近信号线阻断，导致C11减小而C12增加，而CL=C11+C12没有大的变化；

2. 如下右图所示，当信号线靠近时，L11和L12也发生了变化，由于邻近导线的感应涡流，L11将略有减小，L12将增加；

3. 所以两条信号线间距越小耦合越强，大致结论如下：

1, 间距最小情况下（1w），耦合程度<15%；

2, 间距>2w时，耦合度降低到了1%。

4. 当两条传输线相距很远时，线路1的特征阻抗与线路2完全没关系，其特征阻抗与C11成反比（Z0=√(L/C)）；但两条信号线距离非常近时，相邻信号线路2的存在会影响线路1的阻抗（邻近效应）；线路1的阻抗由负载电容决定：Z0 与1/CL成正比；

5. 根据如上分析，此时传输线2上信号状态不同，会影响差分对阻抗的大小：

1, 假设线路2被固定在0电位：那么线路1的单端特征阻抗基本不变（如上图CL变化不大）；

2, 假设线路2被驱动与线路1信号相反：由于线路1与返回路径和线路2之间存在dV11/dt和dV12/dt ，于是产生两个分别穿过电容C11和C12的电流，而线路1与线路2之间变化的电压是2倍单端信号电压：V12=2*V11；那么线路1上的电流：

；线路1阻抗随间距的减小而减小；

3, 假设给线路2被驱动与线路1信号相同：那么两条信号线之间不存在电压差，只有电容C11存在，此时流经线路1的电流为：

，线路1阻抗随间距的减小而增加；

4, 我们从上面的分析得到结论：当差分信号沿差分对传输时，其阻抗仍然是每条信号线单端阻抗的串联（2倍）；同时在两条信号线之间驱动差分信号时，每条信号线的阻抗为因为彼此间耦合而减小；如下所示最小距离耦合时差分阻抗减小约12%。

2，差分对回流分布

我们再从差分信号回流的角度来分析差分阻抗，当两条微带线差分对间距大于3倍线宽时，线间耦合度会很小；如下图中假设两条传输线线路1与线路2电流方向相反：

1. 将线路1和线路2看成单端信号：其回流分布在各自线路下方，不会相互重叠，阻抗相互独立；

2. 将线路1和线路2看成差分信号：可以看成线路1和线路2之间相互回流，即等量的电流从线路1/2流出到线路2/1；其下方回流平面上的总回流为0（Zdiff = Z0 * 2）；

3. 单端阻抗表示的是：传输线相对于回流平面的阻抗特性，增加线路1和线路2与平面之间的距离，单端阻抗会增加；

4. 差分阻抗表示的是：线路1与线路2之间的阻抗特性，当增加线路1和线路2与平面之间的距离，差分阻抗也会发生变化；

5. 如下右图所示，当距离h不断增加，如果返回平面距信号线足够远：差分信号（线路1和线路2）返回平面电流分布会相互重叠并完全抵消，两条信号线将完全相互回流，此时回流路径平面不会再影响到差分阻抗，差分阻抗将保持不变；但单端阻抗取决于线路1或线路2相对于平面之间的回流，随着距离的增加阻抗不断变大。

——返回平面距离信号线足够远：经验法则是信号线与返回路径平面间距离大于或等于两条信号线外边缘之间的跨度。

从上分析可以得到结论：

1. 当信号线与返回平面之间的耦合度大于两条信号线之间的耦合度时：返回路径平面中出现明显的返回电流，返回平面对差分阻抗起到重要作用；

2. 当两条信号线之间的耦合度远大于信号线与返回平面之间的耦合度时：平面中的大部分返回电流会叠加、抵消，此时就算将返回平面去掉不会影响到差分阻抗，例如连接器管脚。

说到这里，似乎、好像、可能出现了一个明显的矛盾：在上一节中说，差分阻抗是单端阻抗的两倍，但为什么现在又说单端阻抗可能会大于差分阻抗呢？

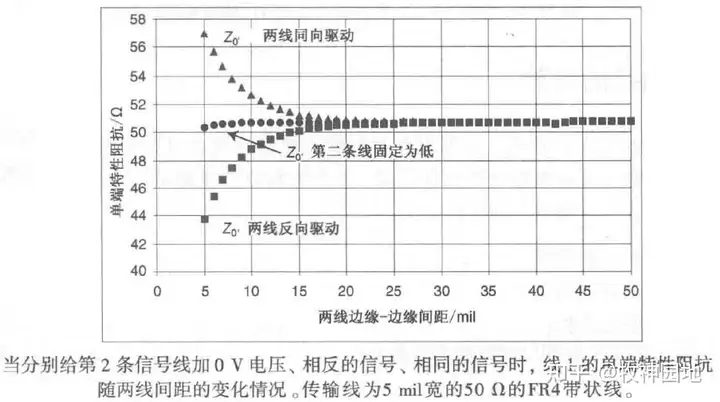
1. 我们首先需要明确的是，在本节中所说的单端阻抗与上一节所说的单端阻抗是两个不同的概念；再来回顾一下“耦合”这一节中关于单端阻抗的描述，如下图所示：当差分对两条信号线不同的驱动模式下，其单端阻抗表现是不一样的；

2. 本节中所说的单端阻抗是指：一条信号线有信号驱动，而第二条信号线保持固定电平；这种情况下信号线的特征阻抗不会随差分对之间距离的变化而变化，单端阻抗只跟回流平面之间的距离（还有介电常数）相关；

3. 在上节所说的单端阻抗是指：特定电压驱动方式（两线反向驱动）下的单端阻抗；所以它跟差分对之间的距离有关；即在相同电压驱动模式下，差分阻抗是单端阻抗的2倍。

注：本文转自https://zhuanlan.zhihu.com/p/598815485，经整理而成。