⭐️ 本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 和 BaguTree Pro 知识星球提问。
学习数据结构与算法的关键在于掌握问题背后的算法思维框架,你的思考越抽象,它能覆盖的问题域就越广,理解难度也更复杂。在这个专栏里,小彭与你分享每场 LeetCode 周赛的解题报告,一起体会上分之旅。
本文是 LeetCode 上分之旅系列的第 36 篇文章,往期回顾请移步到文章末尾~
周赛 356
T1. 满足目标工作时长的员工数目
- 标签:模拟
T2. 统计完全子数组的数目
- 标签:滑动窗口、散列表
T3. 包含三个字符串的最短字符串
- 标签:贪心、全排列、前后缀分解、KMP
T4. 统计范围内的步进数字数
- 标签:数位 DP、记忆化
T1. 满足目标工作时长的员工数目
https://leetcode.cn/problems/number-of-employees-who-met-the-target/
题解(模拟)
简单模拟题。
class Solution {
public:
int numberOfEmployeesWhoMetTarget(vector<int>& hours, int target) {
int ret = 0;
for (int i = 0; i < hours.size(); i++) {
if (hours[i] >= target) ret++;
}
return ret;
}
};
class Solution:
def numberOfEmployeesWhoMetTarget(self, hours: List[int], target: int) -> int:
return sum(e >= target for e in hours)
复杂度分析:
- 时间复杂度:$O(n)$ 线性扫描;
- 空间复杂度:$O(1)$ 仅使用常量级别空间。
T2. 统计完全子数组的数目
https://leetcode.cn/problems/count-complete-subarrays-in-an-array/
题解一(枚举子数组 + 散列表)
枚举子数组,求满足条件的子数组数
class Solution {
public:
int countCompleteSubarrays(vector<int>& nums) {
int n = nums.size();
int ret = 0;
// 目标元素个数
int target = unordered_set<int>(nums.begin(), nums.end()).size();
// 枚举子数组
for (int i = 0; i < nums.size(); i++) {
unordered_set<int> curSet;
for (int j = i; j < nums.size(); j++) {
curSet.insert(nums[j]);
if (curSet.size() == target) {
ret += n - j;
break;
}
}
}
return ret;
}
};
复杂度分析:
- 时间复杂度:$O(n^2)$ 枚举子数组时间;
- 空间复杂度:$O(n)$ 散列表空间。
题解二(滑动窗口 + 散列表)
在题解一中,当子数组的满足条件时,我们不再需要扩展右指针 j,其实左指针 i 也类似。当存在子数组 [i, j] 满足条件时,我们可以收缩左指针到 [i+1, j],如果子数组依然满足条件,则可以继续记录子数组个数 n - j 个。
class Solution {
public:
int countCompleteSubarrays(vector<int>& nums) {
int n = nums.size();
int ret = 0;
// 目标元素个数
int target = unordered_set<int>(nums.begin(), nums.end()).size();
// 滑动窗口
unordered_map<int, int> cnts;
int i = 0;
for (int j = 0; j < nums.size(); j++) {
cnts[nums[j]]++;
while (cnts.size() == target) {
ret += n - j;
if (--cnts[nums[i]] == 0) cnts.erase(nums[i]);
i++;
}
}
return ret;
}
};
复杂度分析:
- 时间复杂度:$O(n)$ 滑动窗口的 i 指针和 j 指针最多移动 n 次;
- 空间复杂度:$O(n)$ 散列表空间。
相似题目:
T3. 包含三个字符串的最短字符串
https://leetcode.cn/problems/shortest-string-that-contains-three-strings/
题解一(贪心)
首先,合并字符串 a 和字符串 b 可以用前后缀分解来模拟:a 的最长后缀与 b 的最长前缀匹配,得到的合并字符串是最短的。而对于目标答案的合并方案来说,必然是 [a, b, c] 的全排列中的一种:
- a + b + c
- a + c + b
- b + a + c
- b + c + a
- c + a + b
- c + b + a
虽然,严谨来说局部贪心是错误的(即先将 a 和 b 合并得到最短字符串 ab,再将 ab 与 c 合并)。例如以下测试用例,这说明在第一次合并中选择最短的字符串,不一定是全局最短的字符串。但是,最优解必然可以通过全排列中的其他方案获得。因此,直接使用 “局部贪心” 即可。
a = "cdaa"
b = "aaef"
c = "daaae"
# a + b + c 其中 a + b = "cdaaef",无法与 c 合并得到最优解 “cdaaaef”
# a + c + b 可以得到最优解 “cdaaaef”
class Solution:
def minimumString(self, a: str, b: str, c: str) -> str:
def merge(a: str, b: str) -> str:
if b in a: return a
for i in range(min(len(a), len(b)), 0, -1):
# 前后缀对比
if a[-i:] == b[:i]:
return a + b[i:]
return a + b
ret = ""
for a, b, c in permutations((a, b, c)):
temp = merge(merge(a,b), c)
# 优先最短字符串,再考虑字典序最小
if (ret == "" or len(temp) < len(ret) or (len(temp) == len(ret) and temp < ret)):
ret = temp
return ret
复杂度分析:
- 时间复杂度:$O(n^2)$ 单次合并的时间复杂度是 $O(n^2)$;
- 空间复杂度:$O(n)$ 临时字符串空间。
题解二(KMP)
题解一时间复杂度的瓶颈在 merge 函数,对于两个字符串的最长的前后缀匹配长度,这正好就是 KMP 算法中求解 next 数组的步骤,而 KMP 算法的时间复杂度是 O(n),存在优化空间。
- next[i] 的含义:s[:i] 的后缀与前缀的最长匹配长度
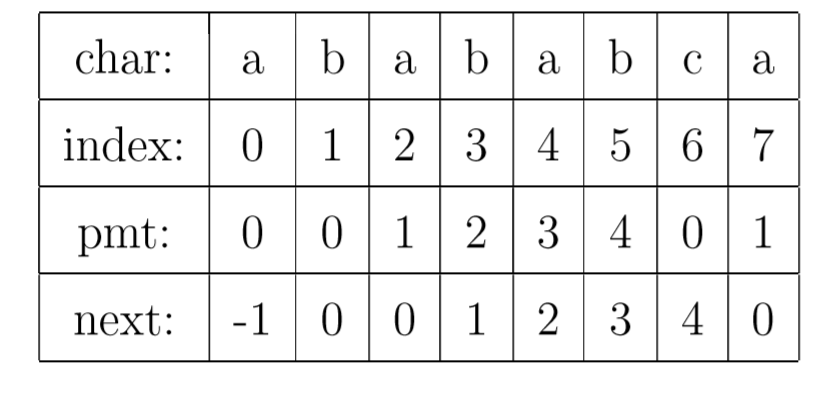
另外还有一个细节,在合并 a 和 b 时我们在中间插入分隔符 “#”,这是为了避免匹配长度大于 a 或 b的长度。例如:
a = "cac"
b = "aca"
# 那么 a + b = "cacaca" 会出现匹配长度大于 a 或 b的长度
class Solution:
def minimumString(self, a: str, b: str, c: str) -> str:
def merge(a: str, b: str) -> str:
if b in a: return a
# 拼接字符串,以计算 b 的后缀与 a 的前缀的匹配长度
s = a + "#" + b
# KMP 求 next 数组
j, next = 0, [0] * len(s)
for i in range(1, len(s)):
while j > 0 and s[i] != s[j]:
j = next[j - 1]
if s[i] == s[j]:
j += 1
next[i] = j
# next[-1]: s[-1] 的最长匹配前缀
return b + a[next[-1]:]
ret = ""
for a, b, c in permutations((a, b, c)):
temp = merge(merge(a,b), c)
# 优先最短字符串,再考虑字典序最小
if (ret == "" or len(temp) < len(ret) or (len(temp) == len(ret) and temp < ret)):
ret = temp
return ret
复杂度分析:
- 时间复杂度:$O(n)$ 单次合并的时间复杂度是 $O(n)$;
- 空间复杂度:$O(n)$ 临时字符串空间。
T4. 统计范围内的步进数字数目
https://leetcode.cn/problems/count-stepping-numbers-in-range/
题解(数位 DP + 记忆化)
相对标准的数位 DP 模板题。
- 1、数位 DP: 我们定义 dp[i, pre, isNumber, isLimit] 表示从第 i 位开始的合法方案数,其中:
- pre 表示上一个数位选择的值;
- isNumber 表示已填数位是否构造出合法数字;
- isLimit 表示当前数位是否被当前数位的最大值约束。
- 2、差值: 由于题目输入是字符串,要计算出 [low, high] 之间的合法方案数,我们可以计算出 [0, high] 和 [0, low] 之间合法方案数的差值,我们可以再单独判断 low 是否合法。
- 3、记忆化: 对于相同 dp[i, …] 子问题,可能会重复计算,可以使用记忆化优化时间复杂度:
class Solution {
val MOD = 1000000007
fun countSteppingNumbers(low: String, high: String): Int {
// 数位 DP
return ((f(high) - f(low) + if (check(low)) 1 else 0) + MOD) % MOD
}
private fun f(num: String): Int {
val memo = Array(num.length) { Array(10) { IntArray(2) { -1 } } }
return dp(memo, 0, num, '0', false, true)
}
private fun check(num: String) : Boolean {
for (i in 1 until num.length) {
if (Math.abs(num[i] - num[i - 1]) != 1) return false
}
return true
}
// dp[i, pre, isNumber]
private fun dp(memo: Array<Array<IntArray>>, i: Int, high: String, pre: Char, isNumber: Boolean, isLimit: Boolean): Int {
// 终止条件
if (i == high.length) {
return if (isNumber) 1 else 0
}
// 读备忘录
if (!isLimit && -1 != memo[i][pre - '0'][if (isNumber) 1 else 0]) {
return memo[i][pre - '0'][if(isNumber) 1 else 0]
}
var ret = 0
val lower = '0'
val upper = if (isLimit) high[i] else '9'
for (choice in lower .. upper) {
if (!isNumber || Math.abs(choice - pre) == 1) {
ret = (ret + dp(memo, i + 1, high, choice, isNumber || choice != '0', isLimit && choice == upper)) % MOD
}
}
if (!isLimit) memo[i][pre - '0'][if (isNumber) 1 else 0] = ret
return ret
}
}
复杂度分析:
- 时间复杂度:$O(nC·C)$ 其中 n 为数位长度,C 为字符集大小 ,总共有 n·C 个子状态,每个子状态的时间复杂度是 $O(C)$,整体时间复杂度是 $O(n·C^2)$
- 空间复杂度:$O(n·C)$ 记忆化空间。
推荐阅读
LeetCode 上分之旅系列往期回顾:
⭐️ 永远相信美好的事情即将发生,欢迎加入小彭的 Android 交流社群~