1 贝叶斯优化的基本原理
贝叶斯优化方法是当前超参数优化领域的SOTA手段,可以被认为是当前最为先进的优化框架,它可以被应用于AutoML的各大领域,不止限于超参数搜索HPO的领域,更是可以被用于神经网络架构搜索NAS以及元学习等先进的领域。现代几乎所有在效率和效果上取得优异成果的超参数优化方法都是基于贝叶斯优化的基本理念而形成的,因此贝叶斯优化是整个AutoML中学习的重点。
然而,虽然贝叶斯优化非常强大,但整体的学习难度却非常高。在学习贝叶斯优化之前,学习者不仅需要充分理解机器学习的主要概念和算法、熟悉典型的超参数优化流程,还需要对部分超出微积分、概率论和线性代数的数学知识有所掌握。特别的是,贝叶斯优化算法本身,与贝叶斯优化用于HPO的过程还有区别。在我们课程有限的时间内,我将重点带大家来看贝叶斯优化用于HPO的核心过程。
首先,我们不理会HPO的问题,先来看待下面的例子。假设现在我们知道一个函数\(f(x)\)以及其自变量\(x\)的定义域,并且我们知道函数\(f(x)\)是相对均匀、平稳的函数,并不会出现突然升高或突然下降的情况。现在,我们希望求解出\(x\)的取值范围上\(f(x)\)的最小值,你打算如何求解这个最小值呢?
面对这一问题,我们有一个通俗的解法,那就是将全域的\(x\)带入\(f(x)\)计算出所有\(f(x)\)可能的结果,一旦整个\(f(x)\)的结果被计算出来,那\(f(x)\)的最小值也就一目了然了。
然而,现在的函数\(f(x)\)是一个异常复杂的函数,计算量非常大、需要的时间也很长,同时我们的计算资源非常紧张,最多只能在函数\(f(x)\)上尝试20次左右,所有我们不太可能将全域\(x\)都带入进行计算,然后再求解最小值。于是我们选择在\(x\)的定义域上随机选择了4个点,并将4个点带入\(f(x)\)进行计算,得到了如下结果:
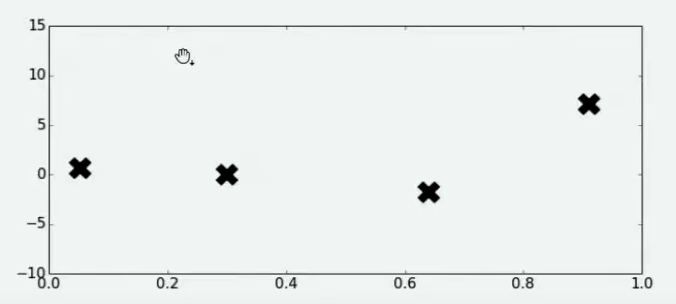
好了,现在有了这4个观测值,你能告诉我\(f(x)\)的最小值在哪里吗?你认为最小值点可能在哪里呢?大部分人会倾向于认为,最小值点在已观测出的\(f(x)\)值中,最小的那个值的附近,但也有许多人不这么认为。当我们有了4个观测值,并且知道我们的函数时相对均匀、平稳的函数,那我们可能对函数的整体分布有如下猜测:
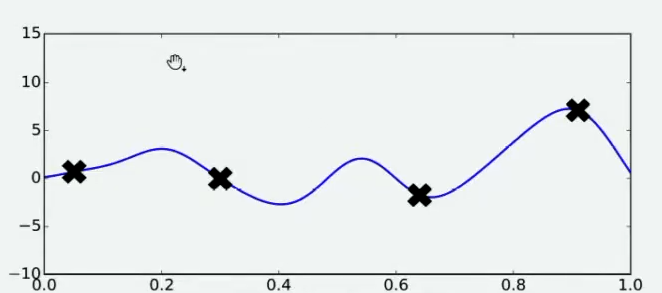
当我们对函数整体分布有一个猜测时,这个分布上一定会存在该函数的最小值。同时,不同的人可能对函数的整体分布有不同的猜测,不同猜测下对应的最小值也是不同的。
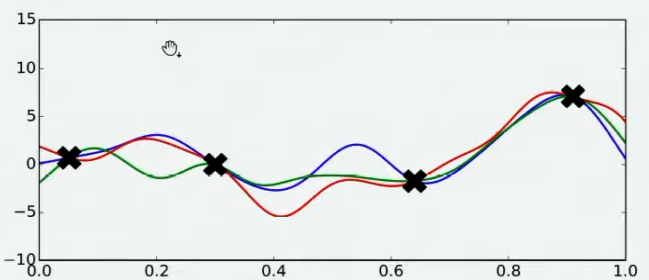
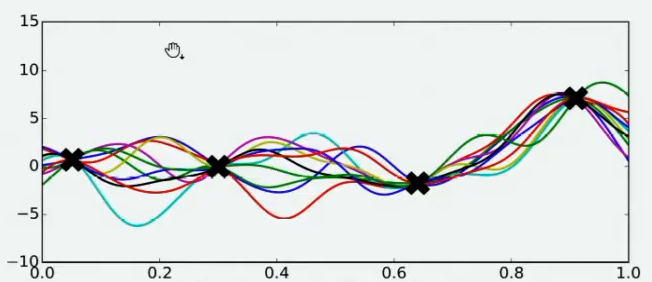
现在,假设我们邀请了数万个人对该问题做出猜测,每个人所猜测的曲线如下图所示。不难发现,在观测点的附近,每个人猜测的函数值差距不大,但是在远离远侧点的地方,每个人猜测的函数值就高度不一致了。这也是当然的,因为观测点之间函数的分布如何完全是未知的,并且该分布离观测点越远时,我们越不确定真正的函数值在哪里,因此人们猜测的函数值的范围非常巨大。
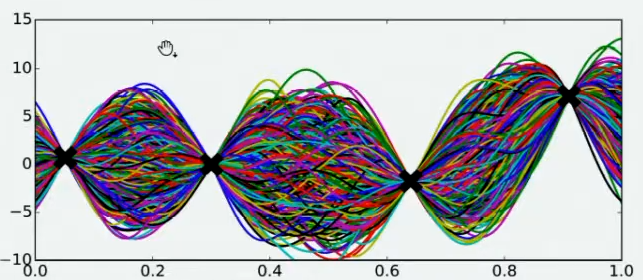
现在,我们将所有猜测求均值,并将任意均值周围的潜在函数值所在的区域用色块表示,可以得到一条所有人猜测的平均曲线。不难发现,色块所覆盖的范围其实就是大家猜测的函数值的上界和下界,而任意\(x\)所对应的上下界差异越大,表示人们对函数上该位置的猜测值的越不确定。因此上下界差异可以衡量人们对该观测点的置信度。
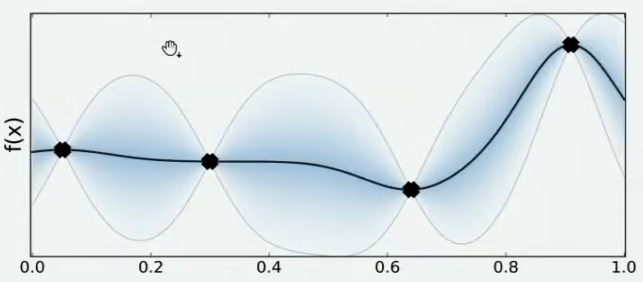
在观测点周围,置信度总是很高,远离观测点的地方,置信度总是很低,所以如果我们能够在置信度很低的地方补充一个实际的观测点,我们就可以很快将众人的猜测统一起来。当整个函数上的置信度都非常高时,我们可以说我们得出了一条与真实的\(f(x)\)曲线高度相似的曲线。并且,观测点越多,我们估计出的曲线会越接近真实的\(f(x)\)。然而,由于计算量有限,我们每次进行观测时都要非常谨慎地选择观测点。那现在,如何选择观测点才能够最大程度地帮助我们找到\(f(x)\)上的最小值呢?
有非常多的方法,其中最简单的手段是使用最小值出现的频数进行判断。由于不同的人对函数的整体分布有不同的猜测,不同猜测下对应的最小值也是不同的,根据每个人猜测的函数结果,我们在\(X\)轴上划将定义域区间进行均匀的划分,如果有某个猜测的最小值落在其中一个区间中,我们就对该区间进行计数。当有数万个人进行猜测之后,我们同时也绘制了基于\(X\)轴上不同区间的频数图,频数越高,说明猜测最小值在该区间内的人越多,反之则说明该猜测最小值在该区间内的人越少。
当我们绘制出频数图之后,很明显,我们知道最小值最有可能在的区间就在x=0.7左右的位置。当我们不取新的观测点时,现在\(f(x)\)上可以获得的可靠的最小值就是x=0.6时的点,但我们如果在x=0.7处取新的观测值,我们就很有可能找到比当前x=0.6的点还要小的\(f_min\)。因此,我们可以就此决定,在x=0.7处进行观测。
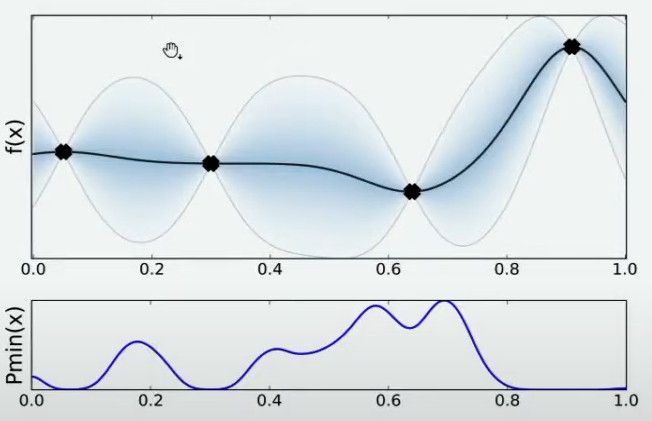
当我们在x=0.7处取出观测值之后,我们就有了5个已知的观测点。现在,我们再让数万人根据5个已知的观测点对整体函数分布进行猜测,猜测完毕之后再计算当前最小值频数最高的区间,然后再取新的观测点对\(f(x)\)进行计算。当允许的计算次数被用完之后(比如,20次),整个估计也就停止了。
你发现了吗?在这个过程当中,我们其实在不断地优化我们对目标函数\(f(x)\)的假设,虽然没有对\(f(x)\)进行全部定义域上的计算,也没有找到最终确定一定是\(f(x)\)分布的曲线,但是随着我们观测的点越来越多,我们对函数的估计是越来越准确的,因此也有越来越大的可能性可以估计出\(f(x)\)真正的最小值。这个优化的过程,就是贝叶斯优化。
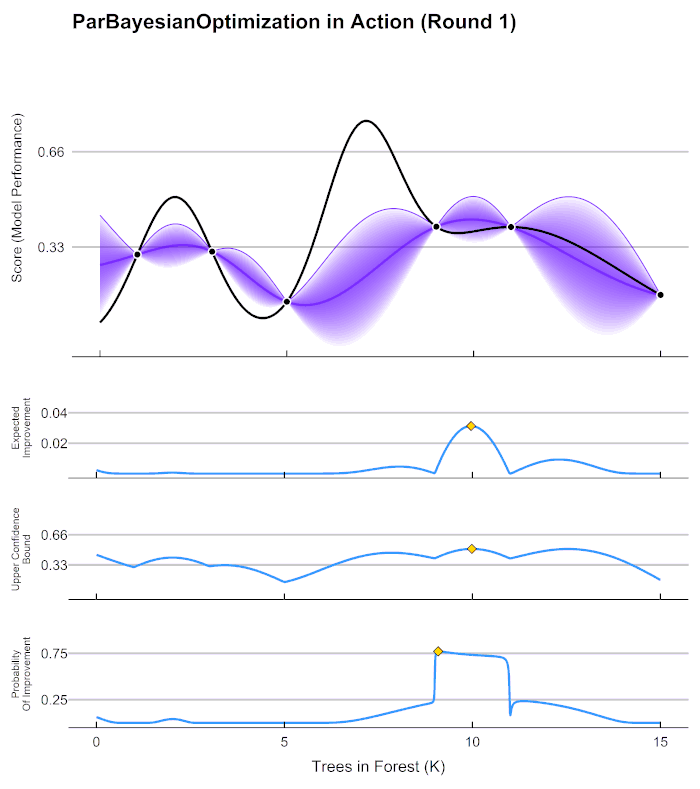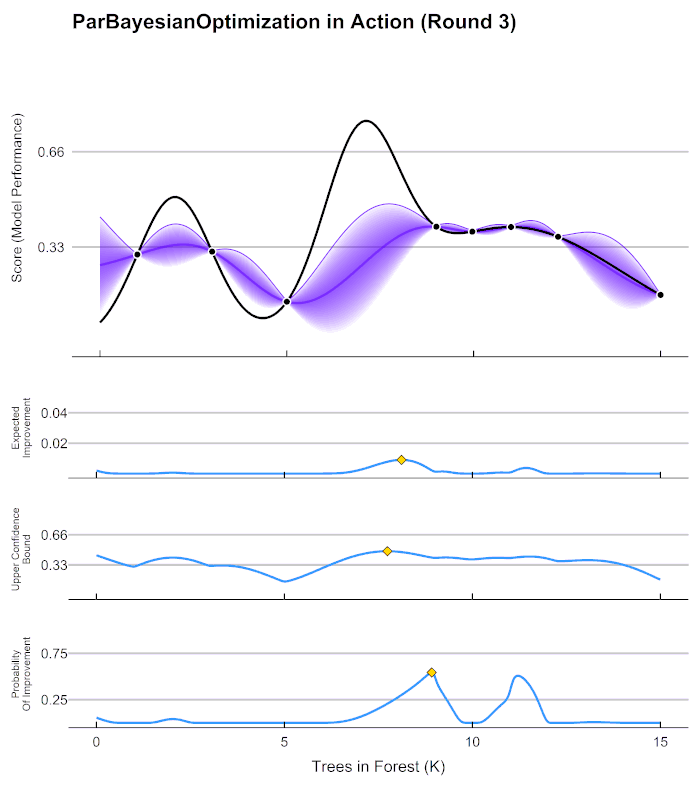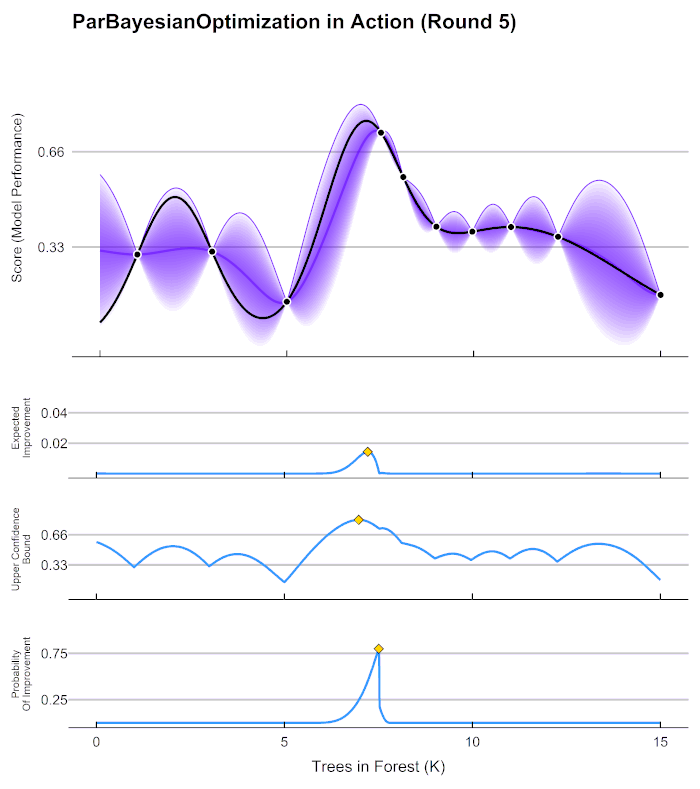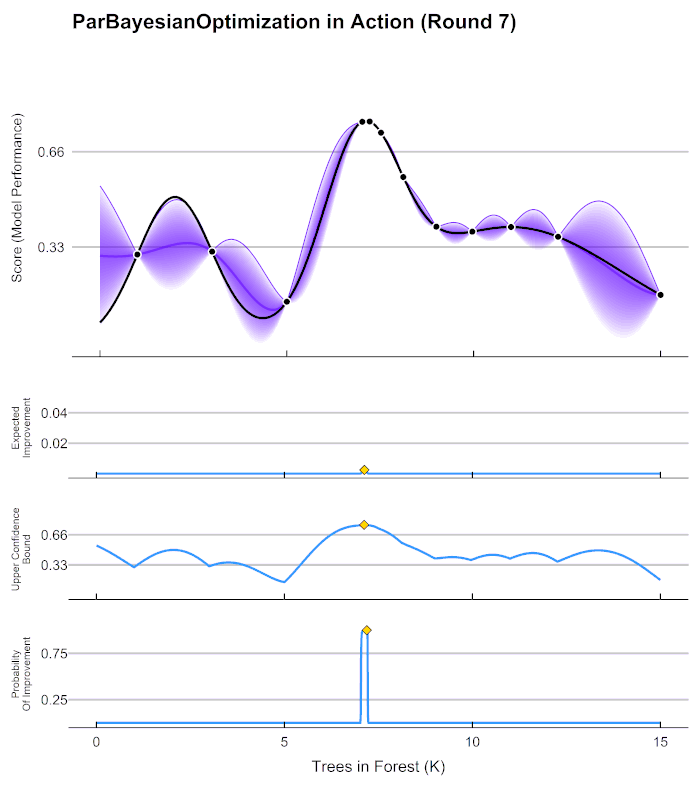
在贝叶斯优化的数学过程当中,我们主要执行以下几个步骤:
-
1 定义需要估计的\(f(x)\)以及\(x\)的定义域
-
2 取出有限的n个\(x\)上的值,求解出这些\(x\)对应的\(f(x)\)(求解观测值)
-
3 根据有限的观测值,对函数分布进行假设(该假设被称为贝叶斯优化中的先验知识),得出该假设分布上的目标值
-
4 定义某种规则,确定下一个需要计算的观测点
并持续在2-4步骤中进行循环,直到假设分布上的目标值达到我们的标准,或者所有计算资源被用完为止。以上流程又被称为序贯模型优化(SMBO),是最为经典的贝叶斯优化方法。
在实际的运算过程当中,尤其是超参数优化的过程当中,有以下具体细节需要注意: