初赛内容 : 数学
三角函数
定义
三角函数是数学中属于初等函数中的超越函数的函数。它们的本质是任何角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的。其定义域为整个实数域。另一种定义是在直角三角形中,但并不完全。现代数学把它们描述成无穷数列的极限和微分方程的解,将其定义扩展到复数系。
三角函数公式看似很多、很复杂,但只要掌握了三角函数的本质及内部规律,就会发现三角函数各个公式之间有强大的联系。而掌握三角函数的内部规律及本质也是学好三角函数的关键所在。
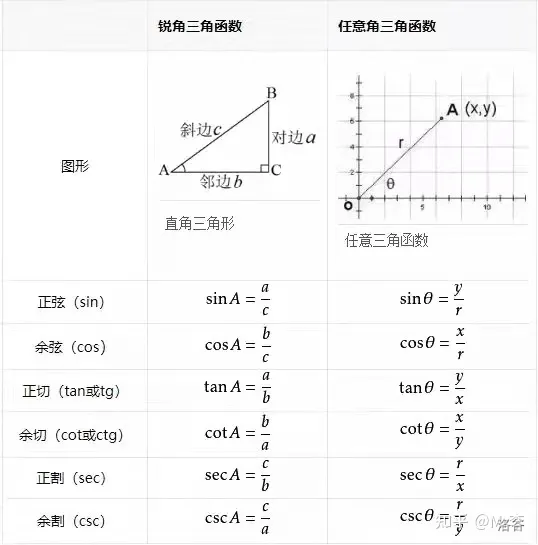
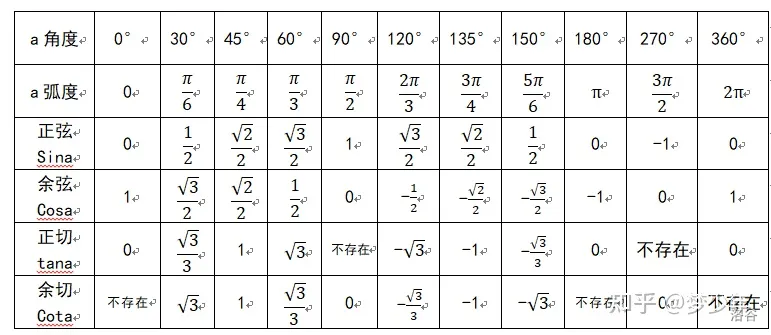
三角函数特殊值
对数函数
定义
对数函数(Logarithmic Function)是以幂(真数)为自变量,指数为因变量,底数为常量的函数。
对数函数是 \(6\) 类基本初等函数之一。其中对数的定义:
如果 \(a^x =N\)(\(a>0\),且 \(a≠1\)),那么数 \(x\) 叫做以 \(a\) 为底 \(N\) 的对数,记作 \(x=log_aN\),读作以 \(a\) 为底 \(N\) 的对数,其中 \(a\) 叫做对数的底数,\(N\) 叫做真数。
一般地,函数 \(y=log_aX\)(\(a>0\),且 \(a≠1\))叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数。
其中 \(x\) 是自变量,函数的定义域是 \((0,+∞)\),即 \(x > 0\)。它实际上就是指数函数的反函数,可表示为 \(x = a^y\)。因此指数函数里对于 \(a\) 的规定,同样适用于对数函数。
“log”是拉丁文logarithm(对数)的缩写,读作:[英][lɔɡ][美][lɔɡ, lɑɡ]。
对数函数特殊值
对数函数的特殊值 对数函数在数学学科中起着重要的作用,在各个领域均有广泛应用。 对数函数以对数底为底数,输入实数,通过公式 \(y = log_a (x)\) 将实数 \(x\) 映射为实数y。 对于一个数学函数而言,对数函数的特殊值具有重要意义。常见对数函数特殊值如下 :
-
\(log_a(1) = 0\)
-
\(log_a(a) = 1\)
-
\(log_a(1/a) = -1\)
-
\(log_a(√a) = 1 / 2\)
-
\(log_a(a^2) = 2\)
数学逻辑运算符
在形式逻辑中,逻辑运算符或逻辑联结词把语句连接成更复杂的复杂语句。例如,假设有两个逻辑命题,分别是“正在下雨”和“我在屋里”,我们可以将它们组成复杂命题“正在下雨,并且我在屋里”或“没有正在下雨”或“如果正在下雨,那么我在屋里”。一个将两个语句组成的新的语句或命题叫做复合语句或复合命题。
集合
概念
集合,简称集,是数学中一个基本概念,也是集合论的主要研究对象。集合论的基本理论创立于19世纪,关于集合的最简单的说法就是在朴素集合论(最原始的集合论)中的定义,即集合是“确定的一堆东西”,集合里的“东西”则称为元素。现代的集合一般被定义为:由一个或多个确定的元素所构成的整体 。
集合的类型
- 有限集和无限集
集合中元素的数目称为集合的基数,集合 \(A\) 的基数记作 \(card(A)\)。当其为有限大时,集合 \(A\) 称为有限集,反之则为无限集。 一般的,把含有有限个元素的集合叫做有限集,含无限个元素的集合叫做无限集。
- 空集
有一类特殊的集合,它不包含任何元素,如 \({x|x∈R x²+1=0}\) ,称之为空集,记为 \(∅\)。空集是个特殊的集合,它有 \(2\) 个特点:
-
空集 \(∅\) 是任意一个非空集合的真子集。
-
空集是任何一个集合的子集。
集合中元素的特性
- 确定性
给定一个集合,任给一个元素,该元素或者属于或者不属于该集合,二者必居其一,不允许有模棱两可的情况出现。
- 互异性
一个集合中,任何两个元素都认为是不相同的,即每个元素只能出现一次。有时需要对同一元素出现多次的情形进行刻画,可以使用多重集,其中的元素允许出现多次。
- 无序性
一个集合中,每个元素的地位都是相同的,元素之间是无序的。集合上可以定义序关系,定义了序关系后,元素之间就可以按照序关系排序。但就集合本身的特性而言,元素之间没有必然的序。
元素与集合的关系
- 属于
如果元素 \(a\) 在集合 \(A\) 中,就说 \(a\) 属于 \(A\),记作 \(a∈A\)。
- 不属于
如果元素 \(a\)不在集合 \(A\) 中,就说 \(a\) 不属于 \(A\),记作 \(a∉A\)。
流程图
(略---)
标签:log,三角函数,元素,第十节,对数函数,集合,动态,规划,定义 From: https://www.cnblogs.com/So-noSlack/p/17569390.html